Recall Energy is the ability to do work:

As machines use energy there is an inevitable loss in the quality of the energy

This is caused by forces:

friction
drag
air resistance
etc.

When objects in contact move - work is done by these forces. This work is transferred to the system which then heats up.

All real mechanical systems produce less useful output work than the energy they take in.

Equivalent amounts of energy do not necessarily have the same capacity to do work.

Consider equal amounts of

electrical energy and
thermal energy.

Electricity can be used for any purpose.
Thermal energy can heat a room.

is difficult to use otherwise.

Ideal machines: convert 100% of the energy input into output energy.

Energy in = Energy out.

Suppose that we do a certain amount of work that is the machine input. Then from our definition of work:

(work)_in = (force)_in x (distance)_in

(work)_out = (force)_out x (distance)_out

Ideal machines obey

(work)_out = (work)_in.

Example: The ideal lever:

work = F₁d₁ = F₂d₂

Levers bend
ropes stretch
friction acts on all machines.

The effect of all these: work is converted to

energy of compression
stretching [returned when we let go!]
thermal energy [which is lost].

Thus, real machines obey the relation:

(work)_out < (work)_in.

Example: a pulley with one end fixed may be used to lift a load.

The force exerted by the person doing the lifting is less than the load if movable pulleys are used because the rope at each side carries the same force T (see Figure). If the person pulls on the rope to lift the load with a constant velocity then F=ma T = 1/2W.

The pulley.

By pulling on one side of the rope to raise the weight the total distance traveled by the rope in the ideal case is twice the height through which the weight is raised.

In the ideal case, then, to raise the weight W, a height h,

the rope must be pulled a distance 2h.

Work done on the weight (the work out) =Wh.
Work done in pulling on rope (work in) = T(2h).

Since T = 1/2W

T(2h) =1/2 W(2h) = Wh.

The input work = the output work.

So some of the input work must be stored in the stretched rope [or be used to battle friction].

• Work done on the weight (the work out) =Wh since the object still has a weight of W and moves a distance h.
  
• Work done in pulling on rope (work in) > T(2h) since a length greater than 2h must be pulled in.

This leads to the concept of efficiency

Power is the rate of doing work:

1kWh = 3.6x10⁶ J
1kWh costs $0.10.

Example: Person Power. Walk up a flight of stairs 3m high in 20s.

mgh = 80kg x 9.8m/s² x 3m = 2350 J
  (=180 lbs x 10 ft = 1800 ft-lbs)

P = 2350 J/20 s = 120 J/s = 120 W
  (=1800 ft-lbs/20 s = 90 ft-lbs/s)

1HP = 550 ft-lbs/sec
so a person does 1/5-1/10 HP!

get a horse to do the work!

The Engine

We consider the external and internal combustion engines, the turbine, and the rocket.

An external combustion engine.

An internal combustion engine.

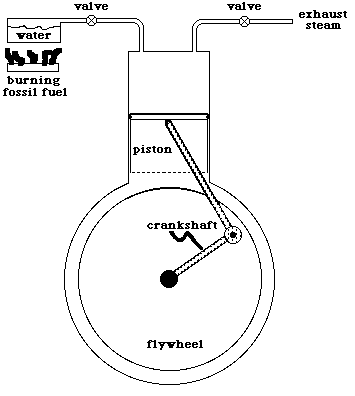
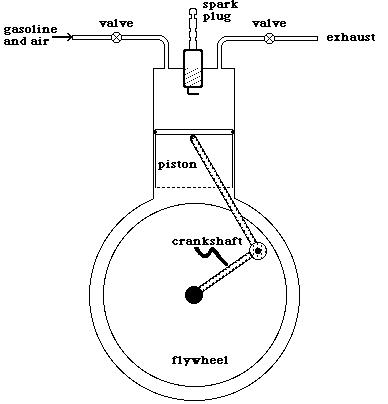
The sequence of events in an internal combustion gasoline engine.

Turbine engines.

The Steam Turbine.

The jet turbine.

The rocket engine.

Electrical energy comes mostly from burning coal or nuclear fuel.

Electricity Generation by Source, 1999 (AER 2000)

it is clean, convenient and safe
it is expensive

There is an electrical force (just like the gravitational force)

F_e = k q₁ q₂/ (distance of separation)²

=(9x10⁹Nm²/C²) q₁ q₂/r²

Now since W = F•d the electric force does work by moving charges.