First Law of Thermodynamics
If we add heat to a system
but do no work on it 
we increase the amount
of energy in the system Lecture VIII
First Law of Thermodynamics If we add heat to a system
but do no work on it
we increase the amount
of energy in the system
If we do work on a system
while adding no heat we also increase the
internal energy.
The inverse of these is also true. These are statements of energy conservation:
this is sometimes written:
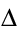Q + W =
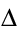U
This is the first law of thermodynamics .
Thermal Energy Thermal energy is just kinetic
energy spread out among all the atoms in a material. That is, the temperature in kelvin is a
direct measure of the random kinetic energy of
molecules. At lower temperature, there is less kinetic energy available for
the average monatomic atom; at higher
temperature, there is more kinetic energy available: Heat transfer The general characteristic of heat transfer:
the
amount of thermal energy available at any temperature
depends on the absolute temperature.
there
must be a temperature difference.
Forms:
Heat Engines Thermal energy is low quality. How can it be used? the heat engine
A heat engine is a machine based on the principle:
Heat is transferred between objects at different temperatures.
A colder object in contact with our skin cools us--it makes us feel cold. A hot object warms us.
A difference in temperature can be made to do work as heat is transferred from the higher to the lower temperature.
Heat engines work on the transfer of heat from a hotter to a cooler object.
An example of a heat engine is a car motor.
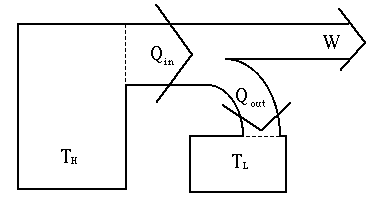
A heat engine
Efficiency Consider the typical heat engine above. The engine: We know we must cool a car's motor. The radiator is part of the car's
cooling system. We have to exhaust waste heat in order to run the motor. The efficiency of this engine can
now be measured. It is the ratio of the amount of work done by
the engine (W) to the total work that the thermal energy at the high
temperature could have done (Qin). Thus, efficiency =
W/Qin and the efficiency in percent is 100% x (W/Qin).
takes in thermal energy
(Qin) at the high temperature (TH)
exhausts thermal
energy (Qout) at a low temperature (TL) does work (W) given by energy
conservation: Qin =
W + Qout The exhaust of waste heat is
a part of the operation of all heat engines.
As we saw above the thermal energy available is proportional to the
absolute temperature. Thus
Qout is proportional to TL
Since W = Qin - Qout the ratio W/Qin is just
efficiency = (Qin - Qout)/Qin = (TH-TL)/TH
Notice that if the heat engine does not have its low temperature reservoir at 0K it can not be 100% efficient. A typical operating range of 400K to 300K would only be 25% efficient!!!!
The heat engine must therefore do something to rid itself of the exhausted thermal energy (waste heat).
As in the car motor, the usual choice for a coolant is water. The reason lies in water's large specific heat.
Heat Capacity Think of the transfer of thermal energy in the form of a liter of
boiling water from a pot to several different objects in sequence: the
temperature rise in the final state is then measured. The objects are
another liter of water at tap
temperature
a bathtub full of tap temperature
water
Lake Erie.
What do we expect:
a noticeable rise in temperature
in the first a very small rise that you might
not be able to measure in the second such a small rise that you
certainly couldn't measure it in the third.
We say that different amounts of water have different heat capacities.
This nomenclature is a remnant of the past, before heat was recognized to be thermal energy in transit from a higher to a lower temperature. In those days, heat was sometimes designated heat energy, what we mean by thermal energy nowadays.
Specific Heat Why are the measured temperatures different in the thought experiment
we just did? What if we could remove the effect of the amount? What is left should
be the same for all water. The specific heat (capacity) is just
the heat capacity divided by the amount of matter measured
in kilograms. For water, this turns out to be 4190 J per kg per degree C. The table
below shows why water is used in this way. Because the amount of water being
heated was different in each case.
Specific heats of various materials.
Material
Specific Heat [J/(kg °C)] Water
4190 Aluminum
910 Table salt
880 Iron
470 Copper
390
Problem of the day: If evapotranspiration from the Earth’s land
area were to diminish by 20% uniformly over the land area, as might result
from widespread removal of vegetation, what changes would occur in the
globally averaged precipitation on the land surface and in the globally
averaged runoff from the land to the sea? Because we need not consider stocks or time constants this is NOT a
residence time problem. So what is it? It is a box model problem. In these type of
problems one must balance the in’s with the out’s. The General Box Model Problem: Conservation Rules
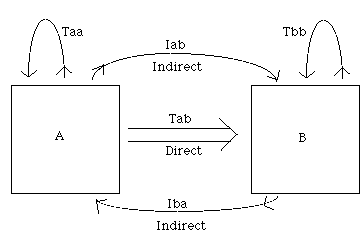
out = in
In Box B: Tbb + Iba = Tab + Iab + Tbb
Simplification
So let us re-define the problem:
The problem can now be restated as how will R, PL change if ELL and ELS both diminish by 20%?
Conservation Rules: There are 3 conservation equations: on sea; on land; land to sea
also we have
So what do we do next? we have 7 variables; but only 3 independent
relations get some information:
the last piece of information we need is that approximately 25% of evapotranspiration from the land precipitates on sea, while 75% precipitates on the land....or
We can then solve to find:
If the reduction is uniformly distributed over the land then it is reasonable to assume:
and so now we have to set up new conservation equations:
and using the modified quantities above for the primed values:
we find:
from which we find: