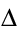Q + W =
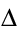U
Lecture IX
Review Heat: Energy in transit from one body to another at a
different temperature Temperature: Temperature is a measure of the thermal energy of
a system. Celsius and Kelvin scales K = 273 +°C First Law of Thermodynamics: Conservation
of Energy
or:
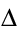Q + W =
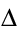U
Statistics of Heat Transfer
We have already discussed the statistical nature of things. This type
of discussion applies to collisional processes - e.g. heat conduction. Gases are composed of atoms or molecules which do not really interact
except through collisions. Suppose we begin with a gas with all the atoms or molecules at the same
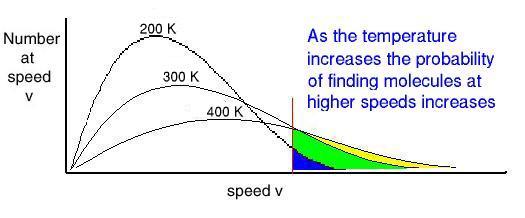
speed. What happens to the speed distribution? In real gases there is a spread of speeds...the distribution is called
the Maxwell-Boltzmann distribution:
constant collisions
a spread of speeds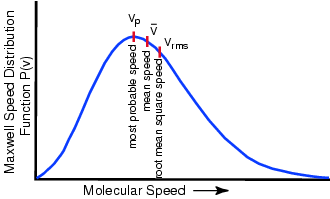
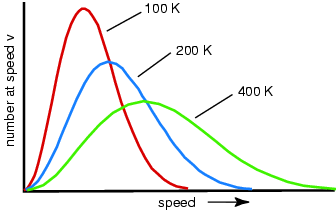
What is the relation between temperature
and the speed distribution? Temperature For a mono-atomic gas (3 degrees of freedom): What happens if you remove the fastest molecules in a liquid? Thermal Energy or
Kinetic Energy
Work and Heat Transfer
Heat transfer
from a warmer to a colder body resembles transfer of water from a high level reservoir to a lower level. Work can be obtained in such a transfer.However the is no way to have water in a reservoir do work while remaining at a single level!
In a similar fashion we must transfer energy from a higher temperature to a lower temperature to do work.
When there is equilibrium there can be no temperature difference. If there is no temperature difference there is no transfer of heat.
Thus it is impossible for a machine to take heat from a reservoir at a certain temperature, to produce work, and to exhaust heat to a reservoir at the same temperature.
In a car we burn gasoline to produce a high temperature.
Entropy Entropy is a measure of disorder in a
system. The entropy in the universe always increases in any process. The only exception occurs when a system is already in equilibrium in
which case any process taking place will leave the system in equilibrium
and thus leave the entropy unchanged. Just because entropy increases does not mean there can never be a
localized entropy decrease. A localized entropy decrease is possible
as long as the entropy of the universe as a whole increases in the
process. Examples: Ice cream Entropy may decrease in a system by the input of energy from an
outside system. A system in equilibrium may be taken out of equilibrium by
doing work on it. Likewise as systems return to equilibrium with their surroundings
useful work may be done.
Second Law of Thermodynamics:
Systems isolated from the rest of the universe will move toward equilibrium with their surroundings.
or
It is impossible for any machine to absorb heat from temperature reservoir, do work, and exhaust heat to a reservoir at the same temperature.
or
All real processes are irreversible
or
...
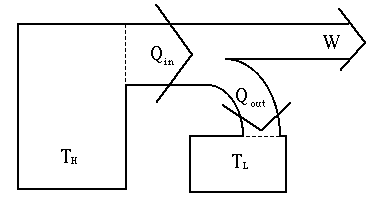
The heat engine.
Maximum Efficiency = W/Qin
Maximum Efficiency = (TH - TL)/TH
Problem of the Day Radioactive radon gas (222Rn) enters an average building
at a rate of one picocurie per second per square meter of foundation area.
Consider a house with a foundation of 200 m2 and an air volume
of 1000 m3. Assume that the house is well designed for energy
conservation so that the ventilation rate is low and only one tenth of
the air in the house is exchanged with outdoor air every hour.
What will be the average steady state
concentration of 222Rn in the house? First recall. Every radioactive isotope has a characteristic time
constant, called its half-life denoted T1/2. If we begin
with N atoms then after one half-life there are N/2 atoms left. This
should reminiscent of the doubling time. Consider a collection of atoms. Suppose at time t, N(t) atoms are
present. The rate of decay of these atoms is proportional to N itself.
The rate of decay is called the
activity and can be written: activity(t) =
Here A curie is an activity of 3.7x1010 decays/s; a
picocurie is an activity of 3.7x10-2 decays/s.
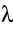N(t)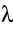 is a
rate constant related to the half-life: =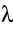
ln 2/T1/2 = 0.693/T1/2
The equilibrium value of N (stock) is determined by setting the rate
of inflow of 222Rn atoms equal to the rate of outflow. The inflow is given by: Fin =
activity/
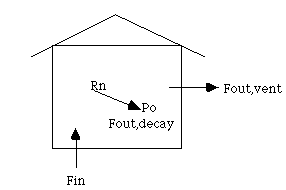
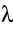
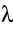
= 7.4 decays/s2/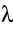
= 7.4 decays/s2/(0.693/T1/2)
= 3.5 x 106 atoms/s
where we have used T1/2 = 3.8 days = 3.3x105 s
The outflow consists of two terms:
N + 0.1N/hr
= N +
2.8x10-5 N/s
= (2.1x10-6 + 2.8x10-5) N/s
= 3.0x10-5 N/s
Setting Fin = Fout we can find N
The steady state concentration will be N/V:
multiplying by 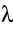we find
246 decays/(m3 s)
or