Basics
The atom has a size of ___m. The nucleus has a size of
10-15m.Lecture XIV
Basics
The atom has a size of ___m.
The nucleus has a size of
10-15m.
All nuclei are constructed
with _____.
Nuclei are bound together by the
strong force.
Because protons and neutrons appear to act identically to the strong force
[even though the proton is electrically charged!], they are often considered
to be interchangeable and are called nucleons, or
nuclear constituents. Only when the distinction is important
do we call them protons or a neutrons. We distinguish nuclei by:
Z atomic number (number of protons)
N number of neutrons
One interesting occurrence is that for existing nuclei as Z increases, N gets larger faster:
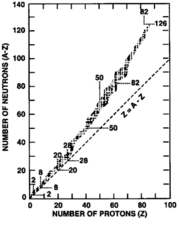
The reason for this is:
protons repel
each other [by what force?] and tend to make nuclei unstable.
The neutrons act to
screen the protons from each
other making the nucleus stable...for effective screening there
needs to be more neutrons than protons
!
When protons and neutrons react together making bonds, they give up
energy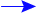 
nuclear binding energy.
The binding energy increases as Z
increases [the proton number]
Example: Hydrogen,
, has no binding energy because it has only one nucleon in its nucleus. Uranium has a very large binding energy, partly because there are two hundred and thirty some nucleons inside the nucleus.
The actual binding energy is not as important as the average binding energy per nucleon. The average binding energy per nucleon is just the total binding energy divided by the number of nucleons. The average binding energy is used because each nucleon actually brought into a nucleus a different binding energy.
Think of balls falling into a hole.
The last ball in falls the least distance into the hole.
The situation for nucleons falling into the nuclear ``well'' is similar to this. Protons and neutrons are more stable inside the nucleus than outside.
Some nuclei have nucleons bound inside them more deeply than others. The average binding energy per nucleon then tells how deeply into the nuclear ``well'' the average nucleon has fallen.
How does the average binding energy per nucleon change as Z increases?
We find that the average binding energy per nucleon first increases up to
iron-56, 
, then
decreases gradually as shown:
The curve shows that nucleons can fall deeper into the nuclear ``well'' in two circumstances:
If a nucleus to the right of
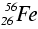breaks into smaller pieces,
the nucleons inside the pieces are deeper inside the ``well'' than
they had been in the original nucleus. - fission
If two nuclei to the left of
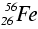combine into a nucleus smaller
than 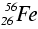, the nucleons inside will
find themselves deeper inside the ``well.'' - fusion
Nuclear fission Nuclear fission is possible for nuclei with large A.
It may happen spontaneously, but generally it occurs because some
activation energy was sent into the nucleus. To get a nuclear
reaction to start, even one that produces useful energy, it is often
necessary to give some energy to the system. The energy provided to
start a reaction going is called the nuclear activation energy. Since there are more neutrons per proton in the large-A nucleus than
in the breakup products, nuclear fission will involve the release of
the extra neutrons. There are many ways for any nucleus to break up,
or fission. After the activation energy has been brought inside the
nucleus by a slow neutron that interacts with the nucleus, the nucleus
acts in a way similar to taffy being pulled. The amount of taffy held in each hand is determined randomly.
Sometimes the right hand will be holding a lot more taffy than the left;
and sometimes the reverse is true.
In a similar way, when a neutron comes in bringing activation energy,
the nucleus is pulled about. It will break up in random ways. Consider as a specific example the fission of uranium-235. One possible
outcome is that the fission will produce strontium-97 and xenon-137: Note: the A's and Z's add up on both sides of the arrow if the reaction
is to proceed!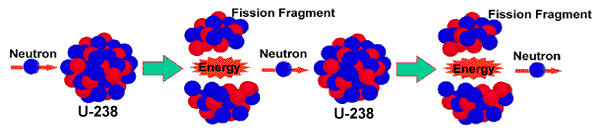
The binding energy curve can be used to find the average binding energy
per nucleon for the nuclei above.
Strontium-97 has a binding energy of 8.6 MeV/nucleon
Xenon-137 has a binding energy of 8.4 MeV/nucleon.
Thus, the total binding energy:
Thus, the nucleons give up the difference between the final total binding energy and the initial binding energy:
The energy appears as kinetic energy of the nuclei and the
neutrons, as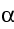 
- and
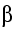- particles, and as
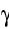-radiation, as well as
neutrinos, massless particles that can carry away energy.
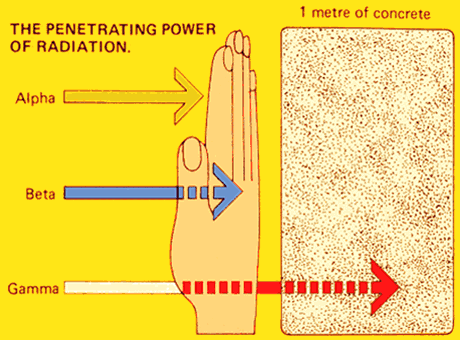
Energy Release
The forces holding the nuclei together are very strong, thus there is a lot of energy released. There is 100 million (108) times as much energy available from the fission of a uranium-235 nucleus as from the burning of a carbon atom.
In addition to the large amount of energy given off in each fission, neutrons are produced in the fission. On the average, 2.43 neutrons are produced from each fission.
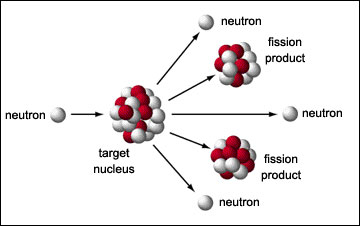
That is, there can be a nuclear chain reaction, just as there can be a chemical chain reaction. The rate of a chemical reaction can be controlled; similarly, the rate of the nuclear reaction can be controlled.
Nuclear fission can be used to produce electricity at slow rates, or can
be used as a bomb, in which case there is an explosively fast chain
reaction. The proportion of uranium-235 [or other fissile material]
is the chief determinant of whether the chain reaction will be explosive or
not. Also important is the ability to let neutrons escape or to capture
them.
| Uranium-235 Concentrations | |
| Natural Uranium | 0.7% |
| Nuclear Reactor Fuel | 4.0% |
| Atomic Bomb | 90% |
Problem of the day It is a project proposed by LANL to produce reactor fuel and electricity
by repeated underground thermonuclear explosion. The proposal is to
detonate 2 devices per day in a mile-deep cavity. How will this work? The nuclear explosive will heat water (1 million tons) in the sealed
cavity to produce superheated steam that would power a regular generating
plant on the surface and also breed fuel in the cavity. If each device has 25 kiloton of explosive at 10% efficiency then we
get a total energy output of: (25 kton/device)(2 devices/day)=50 kton/day from Table 7.1 for dynamite (5.4x106J/kg)(0.91x106kg/kton) =
4.91x1012J/kton (50 kton/day)(4.91x1012J/kton)(0.10) =
2.5x1013J/day (2.5x1013J/day)/(3.6x106J/kWh) =
6.8x106kWh/day which yields (6.8x106kWh/day)(day/24hr) = 280 MW Is this good or bad? It costs $40,000 per 50 kton nuclear device, so the cost of this
electricity is $40,000.00/6.8x106kWh = $0.06/kWh What are some of the other effects?