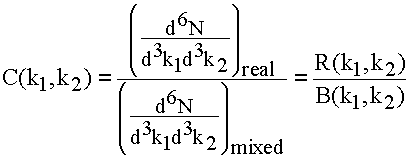 ,
,How to correct the HBT signal for resolution effects:
In HBT, we extract the source geometry (or something related to it…) through the two-particle relative wavefunction, which dictates the probability of measuring a pair with momenta (k1,k2), as compared to the probability of measuring such a pair if they did not know about each other (i.e. the particles did not interact through any effect like Coulomb, strong, or quantum statistics). This latter probability we get from event-mixing, so the correlation is
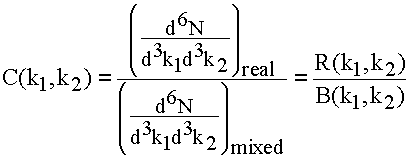 ,
,
where R stands for "real" and B for "background".
Nature puts in this "extra weighting" based on (k1,k2), and if we understand the relative wavefunction, we can get some idea of the source of the particles.
However, we do not measure (k1,k2)—instead we measure (k’1,k’2), where the primes indicate that the momentum we measure has been distorted by resolution. So our signal is distorted. We can correct for this by the following (if we know the resolution in some detail):
We form a correction function
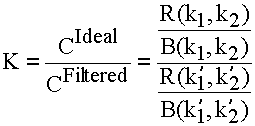 ,
,
where here the unprimed momenta are the "true" ones, and the primed momenta are what we would measure in our detector. The rates (R and B) are obtained by
![]()
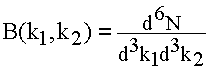
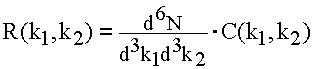
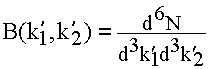
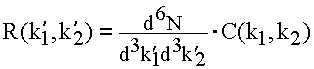
Note:
There is also an additional part of this correction to deal with the Coulomb correction, but I don’t list it here (out of laziness). It follows the same lines.