In this joint work with Aaron Gulliver, we investigate certain construction methods for selfdual ternary codes using a class of conference matrices.Examples are given for lengths up to 96. The codes of length 12, 24, 36 and 48 are equivalent to the Pless symmetry codes. In addition, we have determined that the minimum distance for the codes of length 60 and 84 are the same for both classes. The minimum distance calculations for length 96 (dimension 48) yields 24, improving the previously known bounds according to Brouwer's tables. For the case of length 84, we have determined that the minimum distance of the Pless symmetry code is exactly 21. The relationship between our codes and those of Pless (symmetry codes) is also examined.
Recent results have revealed that Dowling geometries share a number of the nice properties of projective geometries; in some sense the former may be regarded as group-theoretic analogues of the latter. A fundamental result of Rado concerning projective geometries states that every finite geometry representable over a field is representable over a finite field. The corresponding question (posed by Bonin) for Dowling geometries is the following:
Is it true that a finite geometry that embeds in the Dowling geometry of an infinite group, necessarily embeds in a Dowling geometry of a finite group?
In this talk we demonstrate, constructively, that the above question has a negative answer. By way of commentary on the analogy between Dowling and projective geometries, we observe that although our findings contrast with Rado 's result for projective geometries, it is a purely group-theoretic phenomenon tha t settles the matter. This is joint work with Hongxun Qin, Edmund Robertson, and Ákos Seress.
Let ![]() be an
be an ![]() -dimensional vector space over
-dimensional vector space over
![]() , where
, where
![]() ,
, ![]() is a prime. For
is a prime. For
![]() , let
, let
![]() be
the
(0,1)-incidence matrix with rows and columns respectively indexed by the
be
the
(0,1)-incidence matrix with rows and columns respectively indexed by the
![]() - and
- and ![]() -dimensional subspaces of
-dimensional subspaces of ![]() , and with
, and with ![]() -entry equal
to one if and only if the
-entry equal
to one if and only if the ![]() -dimensional subspace
-dimensional subspace ![]() is contained in
the
is contained in
the
![]() -dimensional subspace
-dimensional subspace ![]() . The rank of
. The rank of
![]() was computed
by Yakir and Frumkin over any field not of characteristic
was computed
by Yakir and Frumkin over any field not of characteristic ![]() .
In this talk, we extend their results to
determine the
.
In this talk, we extend their results to
determine the ![]() -adic Smith normal form of
-adic Smith normal form of
![]() for
for
![]() .
.
Applying results from quadratic forms, projective geometries, and recent results of Brouwer and van Dam, we construct the first known amorphic association scheme with negative Latin square type classes where the underlying group structure is not elementary abelian. We give a simple proof of a result of Hamilton that generalized Brouwer's result. We use multiple distinct quadratic forms to construct amorphic association schemes with a large number of classes.
This represents joint work with Qing Xiang.
We will describe some new constructions of ![]() -difference matrices,
-difference matrices, ![]() the cyclic group of order
the cyclic group of order ![]() ,
, ![]() divisible by neither 2 nor 3.
divisible by neither 2 nor 3.
A graph ![]() is path-perfect if there is a positive integer
is path-perfect if there is a positive integer ![]() such that the edge set
such that the edge set ![]() of the graph
of the graph ![]() can be partitioned into paths of length
can be partitioned into paths of length
![]() We prove Fink and Strait's
conjecture: A complete bipartite graph
We prove Fink and Strait's
conjecture: A complete bipartite graph ![]() on
on ![]() vertices
vertices ![]() is path-perfect if and only if there is a positive integer
is path-perfect if and only if there is a positive integer ![]() such that the following two conditions are satisfied;
(i)
such that the following two conditions are satisfied;
(i) ![]() and
(ii)
and
(ii)
![]() This is a joint result with W. Cao.
This is a joint result with W. Cao.
Two linear codes in
![]() are called equivalent if one can be obtained from the other through the actions
of a monomial matrix and an automorphism of
are called equivalent if one can be obtained from the other through the actions
of a monomial matrix and an automorphism of
![]() . Let
. Let ![]() be the number of nonequivalent
be the number of nonequivalent ![]() -dimensional
codes in
-dimensional
codes in
![]() . We describe a method for computing
. We describe a method for computing ![]() . The method relies on the canonical forms
of semi-linear transformations of
. The method relies on the canonical forms
of semi-linear transformations of
![]() , which are characterized by indecomposable skew polynomials over
, which are characterized by indecomposable skew polynomials over
![]() . Some numerical results will be presented.
. Some numerical results will be presented.
Aiso Heinze, in his Ph.D Thesis (Oldenburg, Germany, 2001), has determined all partial difference sets (briefly pds's) over groups of order up to 49. In his research he was using the computer catalogues of strongly regular graphs with a small number of vertices (Ted Spence, University of Glasgow, Scotland),
Among his results was the proof of the existence
of two unusual pds's over groups of order 36,
one of these groups is a direct product of
two copies of dihedral groups of order 6.
Both these pds's imply the same (up to isomorphism)
strongly regular graph ![]() with the parameters
with the parameters ![]() ,
, ![]() ,
,
![]() .
The automorphism group of
.
The automorphism group of ![]() has order 648,
it acts transitively on the vertex set of
has order 648,
it acts transitively on the vertex set of ![]() .
Moreover, it turns out that
.
Moreover, it turns out that ![]() is a Latin square graph,
coming from a proper loop of order 6.
(A loop is called proper if it does not contain
a group in its main class.)
Soon after we realized that A.Barlotti and K.Strambach
were looking for exactly such example of a proper loop
(Advances in Mathematics, 49:1-105, 1983).
is a Latin square graph,
coming from a proper loop of order 6.
(A loop is called proper if it does not contain
a group in its main class.)
Soon after we realized that A.Barlotti and K.Strambach
were looking for exactly such example of a proper loop
(Advances in Mathematics, 49:1-105, 1983).
We managed to get a quite beautiful
computer free interpretation of our result.
Moreover, starting from our construction,
we were able to prove an existence
of an infinite series of proper loops with similar properties.
Our loops have order ![]() , where
, where ![]() is a prime,
equal to 3 modulo 4.
Finally, we will discuss links between our results
and various investigations of many other mathematicians,
including: E. Schoenhardt, A. Sade, R.A. Bailey, C.E. Praeger,
A. Sprague, E. Wilson, R.L. Wilson Jr., E.G. Goodaire & D.A. Robinson, K. Kunen.
is a prime,
equal to 3 modulo 4.
Finally, we will discuss links between our results
and various investigations of many other mathematicians,
including: E. Schoenhardt, A. Sade, R.A. Bailey, C.E. Praeger,
A. Sprague, E. Wilson, R.L. Wilson Jr., E.G. Goodaire & D.A. Robinson, K. Kunen.
In our research we were using computer packages COCO, GAP, GRAPE, nauty.
Using Tree Decompositions and Robertson-Seymour's Excluded Minor Structure
Theorem, we show that a linear (in terms of ![]() ) bound on the
connectivity implies that sufficiently large
graphs will contain
) bound on the
connectivity implies that sufficiently large
graphs will contain ![]() and
and ![]() minors.
In particular, for any
minors.
In particular, for any ![]() , any
, any ![]() -connected sufficiently large graph
must contain a
-connected sufficiently large graph
must contain a
![]() -minor. Moreover, for any
-minor. Moreover, for any ![]() , any
, any ![]() -connected sufficiently
large graph
myst contain a
-connected sufficiently
large graph
myst contain a ![]() -minor. The conjectured connectivity is
-minor. The conjectured connectivity is ![]() .
.
This is joint work with Thomas Boehme, Ken-ichi Kawarabayashi and Bojan Mohar.
Hadwiger's Conjecture states that the chromatic number of any graph is at most the size of the largest clique minor the graph possesses. It is believed that if a counterexample for the conjecture can be found, it should appear in the case of graphs with stability number equal to two, since they have large chromatic number. On the other hand, if the conjecture holds for this case, we obtain further proof that it should hold in general. In this talk, we establish the Hadwiger Conjecture for graphs with stability number two which do not contain induced cycles of size 4 or 5.
Utilizing classical elliptic function invariants, we first sketch our
derivation of several useful new formulas for Ramanujan's ![]() function.
This work includes: the main pair of new formulas for the
function.
This work includes: the main pair of new formulas for the ![]() function that
``separate'' the two terms in the classical formula for the modular
discriminant, a generating function form for both of these formulas,
a Leech lattice form of one of these formulas, and a
triangular numbers form. We then present analogous new formulas for several
other classical cusp forms that appear in quadratic forms, sphere-packings,
lattices and groups.
function that
``separate'' the two terms in the classical formula for the modular
discriminant, a generating function form for both of these formulas,
a Leech lattice form of one of these formulas, and a
triangular numbers form. We then present analogous new formulas for several
other classical cusp forms that appear in quadratic forms, sphere-packings,
lattices and groups.
A binary code with the same weight distribution as its dual is called formally self-dual(f.s.d.). We consider only even f.s.d. codes (all weights even). We show that if C is a Type l (not Type ll) s.d.[n,n/2,2[n/8]]code,with 8/n, then its weight distribution is unique. We determine the possible weight enumerators of a near-extremal f.s.d. even [n,n/2,2[n/8]] code with 8/n as well as the dimension of its radical.
This is joint work with Jon-Lark Kim.
We prove that the only geometry of rank ![]() all of whose proper
contractions are ternary Dowling geometries is the ternary Dowling
geometry. We use this to prove a stronger version of a conjecture of
Joseph Kung and James Oxley.
all of whose proper
contractions are ternary Dowling geometries is the ternary Dowling
geometry. We use this to prove a stronger version of a conjecture of
Joseph Kung and James Oxley.
This is joint work with Tom Dowling.
Vortex structure is a fundamental feature of graph minor structure theory. Perhaps it is also the least understood by the majority of graph theorists. This lecture will be an explanation of what is a vortex and how vortices fit into the structure theory and well-quasi-ordering aspects of graph minor theory.
Back in 1865, Sylvester posed the following fundamental (and
still open) problem in Geometric Probability. For a probability
distribution ![]() in the plane, let
in the plane, let
![]() denote the
probability that four independent
denote the
probability that four independent ![]() -random points form a convex
quadrilateral. What is Sylvester Four Point Problem's Constant
-random points form a convex
quadrilateral. What is Sylvester Four Point Problem's Constant
![]() ? (where the infimum is taken over all
probability distributions with positive Borel measure). It is known that
the problem of finding
? (where the infimum is taken over all
probability distributions with positive Borel measure). It is known that
the problem of finding ![]() is closely related to the problem of
determining
the minimum number of convex quadrilaterals in a finite set of points in
the plane in general position. This problem is in turn closely related to
the rectilinear crossing number of the complete graphs
is closely related to the problem of
determining
the minimum number of convex quadrilaterals in a finite set of points in
the plane in general position. This problem is in turn closely related to
the rectilinear crossing number of the complete graphs ![]() , and also to
the problem of determining the number of
, and also to
the problem of determining the number of ![]() -sets in a finite set
of points in the plane in general position. Recently, we have refined the
best lower bound for
-sets in a finite set
of points in the plane in general position. Recently, we have refined the
best lower bound for ![]() , and have shown that
, and have shown that
![]() . This is joint work with József Balogh.
. This is joint work with József Balogh.
The function lattice, or generalized Boolean algebra, is the set
of ![]() -tuples with the
-tuples with the ![]() th coordinate an integer between 0
and a bound
th coordinate an integer between 0
and a bound ![]() . Two
. Two ![]() -tuples
-tuples ![]() -intersect if they have
at least
-intersect if they have
at least ![]() common nonzero coordinates. We prove a Hilton-Milner
type theorem for systems of
common nonzero coordinates. We prove a Hilton-Milner
type theorem for systems of ![]() -intersecting
-intersecting ![]() -tuples.
-tuples.
This is joint work with P. L. Erdos and L. Székely.
A signed graph is a pair ![]() in which
in which ![]() is a graph and
is a graph and ![]() is a labeling of the edges with elements of the multiplicative group
is a labeling of the edges with elements of the multiplicative group
![]() . A circle in a signed graph is called negative if the product of labels on its edges is negative. Otherwise the circle is called positive. A signed graph is called balanced if all its circles are positive.
. A circle in a signed graph is called negative if the product of labels on its edges is negative. Otherwise the circle is called positive. A signed graph is called balanced if all its circles are positive.
There is a matroid associated with ![]() whose elements are the edges of
whose elements are the edges of ![]() . The rank of a subset
. The rank of a subset ![]() of edges is equal to the number of vertices incident to edges in
of edges is equal to the number of vertices incident to edges in ![]() minus the number of balanced components in the subgraph defined by the
minus the number of balanced components in the subgraph defined by the ![]() .
.
In this talk we will discuss several structural properties of this signed-graphic matroid: representability, topology, connectivity, and decompositions.
This talk presents joint work with Hongxun Qin of The George Washington university.
The problem of generating frequent itemsets arises in the field of Data Mining.
In this problem we are given a data file that may be regarded as a collection
of subsets of some finite universal set. Each member of the universal set is
called an "item". A "frequent itemset" is a set of items that appears at least
![]() times in the data file (for some threshold
times in the data file (for some threshold ![]() ). An important problem in Data
Mining is to compute all frequent itemsets, and numerous algorithms for this
have been given.
). An important problem in Data
Mining is to compute all frequent itemsets, and numerous algorithms for this
have been given.
These algorithms are usually evaluated empirically - their relative execution
time on various data files is reported. Analysis by computational complexity
does not reach much beyond the observation that the worst case execution time
is exponential (at least), since output size is exponential in terms of input
size. We describe a variant of one well known algorithm to compute frequent
itemsets, and sketch a proof that, when ![]() , its execution time is linear in
terms of the sum of output size and input size.
, its execution time is linear in
terms of the sum of output size and input size.
We consider the simple group
![]() and its
automorphism group
and its
automorphism group
![]() each in its classical action
on 9 points. As these actions are known to be non-geometrical in
the sense of D.Betten, we introduce a new notion, ``geometrical
group of second order," which allows us to interpret our groups
each in its classical action
on 9 points. As these actions are known to be non-geometrical in
the sense of D.Betten, we introduce a new notion, ``geometrical
group of second order," which allows us to interpret our groups ![]() and
and ![]() of degree 9 (as well as their corresponding stabilzers of
degree 8) as automorphism groups of suitable collections of
regular uniform incidence structures.
of degree 9 (as well as their corresponding stabilzers of
degree 8) as automorphism groups of suitable collections of
regular uniform incidence structures.
Along the way we are led to consider so-called overlarge sets of
Steiner designs, in particular the overlarge set of nine Steiner
3-designs with parameters ![]() which was initially found by
W.L. Edge and later rediscovered by D.R. Breach and A.P. Street. From here, we give a simple new construction of a
classical partial geometry with parameters
which was initially found by
W.L. Edge and later rediscovered by D.R. Breach and A.P. Street. From here, we give a simple new construction of a
classical partial geometry with parameters
![]() having 120 points, 135 lines and automorphism group
having 120 points, 135 lines and automorphism group ![]() . We also
provide new constructions of the two partial geometries with
parameters
. We also
provide new constructions of the two partial geometries with
parameters
![]() which were characterized by R. Mathon with the aid of a computer.
which were characterized by R. Mathon with the aid of a computer.
This is joint work with M. Klin and S. Reichard.
Smith normal form is a generalization of ![]() -rank. We use
-rank. We use ![]() -adic Jacobi sums, a theorem of Daqing Wan, and some representation of the general linear group to determine the Smith normal forms of designs arising in finite Desarguesian geometries.
-adic Jacobi sums, a theorem of Daqing Wan, and some representation of the general linear group to determine the Smith normal forms of designs arising in finite Desarguesian geometries.
Let ![]() be an odd prime. Let
be an odd prime. Let ![]() be a finite
be a finite ![]() -group and
-group and ![]() be an irreducible character of
be an irreducible character of ![]() . Denote by
. Denote by
![]() the complex conjugate of
the complex conjugate of ![]() . Assume that
. Assume that
![]() . We show that the number of distinct irreducible constituents of the product
. We show that the number of distinct irreducible constituents of the product
![]() is at least
is at least ![]() .
.
Subgroups ![]() and
and ![]() of a finite group
of a finite group ![]() are said to be totally permutable if every subgroup of
are said to be totally permutable if every subgroup of ![]() permutes with every subgroup of
permutes with every subgroup of ![]() . The behaviour of finite pairwise totally permutable products are studied with respect to certain classes of groups including the class of groups where all the subnormal subgroups permute with all the maximal subgroups,the so called
. The behaviour of finite pairwise totally permutable products are studied with respect to certain classes of groups including the class of groups where all the subnormal subgroups permute with all the maximal subgroups,the so called ![]() -groups and also the class of all groups where all the subnormal subgroups are permutable,the so called
-groups and also the class of all groups where all the subnormal subgroups are permutable,the so called ![]() -groups (joint work with Peter Hauck and Hermann Heineken).
-groups (joint work with Peter Hauck and Hermann Heineken).
For a fixed positive integer ![]() , define the Neumann
, define the Neumann ![]() -center of the group
-center of the group ![]() to be the set of all elements
to be the set of all elements ![]() of
of ![]() such that
such that ![]() for all
for all ![]() -subsets
-subsets ![]() of
of ![]() . Define the Freiman center to be the set of all
. Define the Freiman center to be the set of all ![]() in
in ![]() such that for each
such that for each ![]() in
in ![]() , the set
, the set
![]() has at most three distinct elements. We discuss two questions:
has at most three distinct elements. We discuss two questions:
Dowling geometries are a class of finite geometries defined using groups, which share many of the nice properties of projective geometries. A fundamental result of Rado concerning the latter type of geometries states that every finite geometry representable over a field is representable over a finite field. The corresponding question for Dowling geometries is the following:
Is it true that a finite geometry that embeds in the Dowling geometry for an infinite group, necessarily embeds in a Dowling geometry for a finite group?
This question can be reduced to a purely group-theoretic one, which may be stated roughly as follows:
Is it true that every finite partial Cayley table of an infinite group arises as a partial Cayley table of a finite group?
It is demonstrated that this latter question has a negative answer, thereby settling the original embeddability question. This is joint work with Honqxun Qin, Edmund Robertson, and Akos Seress.
in
Given an ![]() -dimensional vector space
-dimensional vector space ![]() over the field of complex numbers and a nondegenerate hermitian form, we consider the set of subspaces of
over the field of complex numbers and a nondegenerate hermitian form, we consider the set of subspaces of ![]() that are either positive-definite or have a further positive-definite subspace of maximal dimension. We define a rank-n geometry on this set (using symmetrized containment as our incidence relation), demonstrate the simple-connectedness of this geometry in most cases, and pose some questions about the automorphism group of this geometry.
that are either positive-definite or have a further positive-definite subspace of maximal dimension. We define a rank-n geometry on this set (using symmetrized containment as our incidence relation), demonstrate the simple-connectedness of this geometry in most cases, and pose some questions about the automorphism group of this geometry.
For ![]() a group, a mapping
a group, a mapping
![]() is called a complete mapping of
is called a complete mapping of ![]() if the mappings
if the mappings
![]() and
and
![]() are both bijections.
are both bijections.
We derive a sufficient condition for a subgroup of ![]() ,
, ![]() the algebraic closure of
the algebraic closure of ![]() , to admit complete mappings. We will use this condition to give new proofs of the existence of complete mappings for some classes of linear groups.
, to admit complete mappings. We will use this condition to give new proofs of the existence of complete mappings for some classes of linear groups.
We say a subgroup property ![]() is closed under joins if
is closed under joins if
![]() and
and
![]() implies that
implies that
![]() . Then if
. Then if ![]() is closed under joins, given any subgroup
is closed under joins, given any subgroup ![]() of a group
of a group ![]() , the
, the ![]() core of
core of ![]() in
in ![]() ,
,
![]() , can be defined to be
, can be defined to be
![]() and
and
![]() , the unique maximal subgroup of
, the unique maximal subgroup of ![]() that has property
that has property ![]() in
in ![]() . Note that if
. Note that if
![]() means
means ![]() is normal in
is normal in ![]() , then
, then
![]() , the normal. We say a subgroup property
, the normal. We say a subgroup property ![]() is closed under intersections if
is closed under intersections if
![]() and
and
![]() implies that
implies that
![]() . Then if
. Then if ![]() is closed under intersections, given any subgroup
is closed under intersections, given any subgroup ![]() of
of ![]() , the
, the ![]() closure of
closure of ![]() in
in ![]() ,
,
![]() , can be defined to be the intersection of all subgroups
, can be defined to be the intersection of all subgroups ![]() of
of ![]() such that
such that ![]() and
and ![]() ; this is the unique minimal subgroup of
; this is the unique minimal subgroup of ![]() that contains
that contains ![]() and has property
and has property ![]() in
in ![]() . Note that if
. Note that if ![]() means
means ![]() is normal in
is normal in ![]() , then
, then
![]() , the normal. We say a subgroup property
, the normal. We say a subgroup property ![]() is a lattice property if it is closed under joins and closed under intersections, so that
is a lattice property if it is closed under joins and closed under intersections, so that
![]() i Theorem 1. Suppose
i Theorem 1. Suppose ![]() is closed under joins,
is closed under joins, ![]() is closed under intersections, and
is closed under intersections, and ![]() is a lattice property. Suppose further that if
is a lattice property. Suppose further that if ![]() , then
, then
![]() and
and ![]() . Then the following are equivalent: When (a) or (b) holds, so that both hold, we will say
. Then the following are equivalent: When (a) or (b) holds, so that both hold, we will say ![]() and
and ![]() are
are ![]() -supplementary. We look at a variety of aspects of this concept, including, given a join-closed
-supplementary. We look at a variety of aspects of this concept, including, given a join-closed ![]() , the existence and determination of the unique weakest intersection-closed property, denoted
, the existence and determination of the unique weakest intersection-closed property, denoted
![]() , such that
, such that ![]() and
and
![]() are
are ![]() -supplementary. We say
-supplementary. We say ![]() and
and
![]() , are
, are ![]() -complementary. Similarly, given an intersection-closed
-complementary. Similarly, given an intersection-closed ![]() , we determine the unique weakest join-closed property,
, we determine the unique weakest join-closed property,
![]() , such that
, such that
![]() and
and ![]() are
are ![]() Theorem 2. Suppose
Theorem 2. Suppose ![]() is in the image of
is in the image of
![]() and
and ![]() is in the image of
is in the image of
![]() . Then
. Then
![]() if and only if
if and only if
![]() .
.
In this talk we investigate the following problem: properties ![]() which transfer (or do not transfer) from all cyclic subgroups, or all abelian subgroups to all arbitrary subgroups. We solve this problem completely when
which transfer (or do not transfer) from all cyclic subgroups, or all abelian subgroups to all arbitrary subgroups. We solve this problem completely when ![]() is the property of having finite index in its normal closure, proving that
is the property of having finite index in its normal closure, proving that ![]() carries from abelian, but not from cyclic to arbitrary subgroups. We use primarily some results of B.H. Neumann.
carries from abelian, but not from cyclic to arbitrary subgroups. We use primarily some results of B.H. Neumann.
This talk does not settle the issue of the existence of such groups. Assuming a first-order language, ![]() , appropriate for group theory, the universal theory of a class of groups is just the set of all universal sentences of
, appropriate for group theory, the universal theory of a class of groups is just the set of all universal sentences of ![]() true for every group in the class. Sometime ago Verena Huber Dyson asked whether or not the universal theory of torsion groups
coincides with the universal theory of finite groups. Here we show that if these theories coincide, then there cannot exist a finitely presented group of prime exponent. We cannot, however, say anything about the converse.
true for every group in the class. Sometime ago Verena Huber Dyson asked whether or not the universal theory of torsion groups
coincides with the universal theory of finite groups. Here we show that if these theories coincide, then there cannot exist a finitely presented group of prime exponent. We cannot, however, say anything about the converse.
A subgroup ![]() of a group
of a group ![]() is called 2-subnormal, or subnormal of defect 2, if there exists a normal subgroup
is called 2-subnormal, or subnormal of defect 2, if there exists a normal subgroup ![]() such that
such that ![]() is normal in
is normal in ![]() . Heineken, Stadelmann, and Mahdavi have extensively studied groups having certain collections of subgroups subnormal of defect 2. Mahdavi looked at the interdependencies between groups having all cyclic, all abelian, all class 2, and all subgroups 2 subnormal. He left as an open question whether an arbitrary group having all class 2 subgroups 2-subnormal implies that all subgroups are 2-subnormal. We construct a group having all class 2 subgroups 2-subnormal, but not having all subgroups 2-subnormal.
. Heineken, Stadelmann, and Mahdavi have extensively studied groups having certain collections of subgroups subnormal of defect 2. Mahdavi looked at the interdependencies between groups having all cyclic, all abelian, all class 2, and all subgroups 2 subnormal. He left as an open question whether an arbitrary group having all class 2 subgroups 2-subnormal implies that all subgroups are 2-subnormal. We construct a group having all class 2 subgroups 2-subnormal, but not having all subgroups 2-subnormal.
We establish a correlation between the structures of a group of power automorphisms of some group and their mutual commutator subgroup and consider the consequences for the norm of a group, and for its capability. (Report on work done by J.Beidleman, H.Heineken and M.Newell)
in
This is joint work (in progress) with R Guralnick. We will prove that if ![]() is a nonparabolic element in a classical simple group then 3 conjugates of
is a nonparabolic element in a classical simple group then 3 conjugates of ![]() generate
generate ![]() . The methods used will be probabilistic in nature relying on Aschbacher characterization of maximal subgroups of classical groups.
. The methods used will be probabilistic in nature relying on Aschbacher characterization of maximal subgroups of classical groups.
The study of 2-characters of a group by Sehgal and the presenter led to the introduction of weak Cayley table maps (WCT maps) between groups.
A map
![]() is a WCT-homomorphism if
is a WCT-homomorphism if
The group of WCT isomorphisms from a group to itself has been studied by Humphries, who proved that for symmetric groups and free groups it is generated by the automorphisms and the map
![]() . A WCT-isomorphism between two groups ensures that they have the same character table and other properties.
. A WCT-isomorphism between two groups ensures that they have the same character table and other properties.
We call a map
![]() is a conjugacy-fuzzy (cf)-homomorphism if
is a conjugacy-fuzzy (cf)-homomorphism if
The weaker property that defines fc maps has produced some surprising results. The cf-isomorphisms need not preserve conjugacy classes and can exist between groups with different character tables. Any permutation which fixes the conjugacy classes of a group setwise is a cf-isomorphism. If we consider the cf-isomorphisms from ![]() to itself there are three kinds of elements.
to itself there are three kinds of elements.
(1) Permutations which fix each conjugacy class.We call such permutations basic standard cf isomorphisms.
(2) cf-isomorphisms which permute conjugacy classes but do not split them.
We call the subgroup of permutations generated by cf-isomorphisms of types (1) and (2) the standard group.
(3) There are non-standard cf isos.
The set of all cf-isomorphisms is not necessarily a group but is a union of cosets of the standard group. We can characterize cf-isomorphisms by the property
We do not, however, have a more intrinsic group theoretical or character theoretical characterization.
Many questions can be posed on the lines of: which groups have only standard
cf maps, do free groups have non-standard maps, what equivalence relation
does ``having a cf-isomorphism between
them'' produce on the set of ![]() -groups.
-groups.
It is well known that the squares of elements in a group do not form a subgroup and that the alternating group on four
letters is minimal with this property. For given ![]() , what is the group of minimal order such that the
, what is the group of minimal order such that the
![]() powers of elements do not form a subroup? For odd
powers of elements do not form a subroup? For odd ![]() , it can be shown that the dihedral group of order
, it can be shown that the dihedral group of order ![]() is a minimal counter-examle, where
is a minimal counter-examle, where ![]() is the smallest prime dividing
is the smallest prime dividing ![]() .
.
If ![]() is even, the situation is more complex. The order of the minimal counter example depends on the odd prime factors
of
is even, the situation is more complex. The order of the minimal counter example depends on the odd prime factors
of ![]() and the exact
and the exact ![]() -power dividing
-power dividing ![]() .
.
Let ![]() be a Hall system of a finite, solvable group
be a Hall system of a finite, solvable group ![]() and let
and let
![]()
![]() denote the set of all
denote the set of all ![]() -permutable subgroups of
-permutable subgroups of ![]() . It is known that
. It is known that
![]()
![]() is a sublattice of the subgroup lattice of
is a sublattice of the subgroup lattice of ![]() . We call
. We call ![]() an
an ![]() -group if the lattice
-group if the lattice
![]()
![]() is modular. (The conjugacy of any two Hall systems implies that the condition
is modular. (The conjugacy of any two Hall systems implies that the condition ![]() is independent of the Hall system chosen).
is independent of the Hall system chosen).
It is evident that if ![]() for all
for all ![]() ,
,
![]()
![]() , then
, then
![]()
![]() is modular. Our principal result is that the converse holds: If
is modular. Our principal result is that the converse holds: If ![]() , then any two
, then any two ![]() -permutable subgroups permute with each other. In addition to the proof of this result, we will discuss closure properties of the class
-permutable subgroups permute with each other. In addition to the proof of this result, we will discuss closure properties of the class ![]() and local-global results (about what happens at each prime).
and local-global results (about what happens at each prime).
Let ![]() be a finite group, and let
be a finite group, and let ![]() be the character degrees of
be the character degrees of ![]() . We consider the graph whose vertex set is the set of primes that divide degrees in
. We consider the graph whose vertex set is the set of primes that divide degrees in ![]() . There is an edge between
. There is an edge between ![]() and
and ![]() if
if ![]() divides some degree in
divides some degree in ![]() . These graphs have been studied in a number of places. In this paper, we classify the graphs that can arise when
. These graphs have been studied in a number of places. In this paper, we classify the graphs that can arise when ![]() is a solvable group of Fitting height 2.
is a solvable group of Fitting height 2.
When ![]() is a finite nonabelian group, we associate the common-divisor graph
is a finite nonabelian group, we associate the common-divisor graph
![]() with
with ![]() by letting nontrivial degrees in
by letting nontrivial degrees in
![]() be the vertices and making distinct vertices adjacent if they have a common nontrivial divisor. A set
be the vertices and making distinct vertices adjacent if they have a common nontrivial divisor. A set ![]() of vertices for this graph is said to be strongly connective for
of vertices for this graph is said to be strongly connective for
![]() if there is some prime which divides every member of
if there is some prime which divides every member of ![]() , and every vertex outside of
, and every vertex outside of ![]() is adjacent to some member of
is adjacent to some member of ![]() . When
. When ![]() has a nonabelian solvable quotient, we show that if
has a nonabelian solvable quotient, we show that if
![]() is connected and has a diameter of at most
is connected and has a diameter of at most ![]() , then indeed
, then indeed
![]() has a strongly connective subset.
has a strongly connective subset.
For a given prime ![]() , what is the smallest integer
, what is the smallest integer ![]() such that there exists a group of order
such that there exists a group of order ![]() in which
the commutators are not a subgroup? In this paper we show that
in which
the commutators are not a subgroup? In this paper we show that ![]() for any odd prime and
for any odd prime and ![]() for
for ![]() (Joint work with Luise-Charlotte Kappe).
(Joint work with Luise-Charlotte Kappe).
Weisner's group theoretic method is applied to obtain new generating functions for Hermite matrix functions ![]() defined by L.Jodar and R.Com-pany, by giving suitable interpretation to the index
defined by L.Jodar and R.Com-pany, by giving suitable interpretation to the index ![]() . The algebraic structure underlying Hermite matrix functions(HMF) can be recognized in full analogy with Hermite functions(HF), thus providing a unifying view to the theory of both HMF's and HF's. A few special cases of interest are also discussed.
. The algebraic structure underlying Hermite matrix functions(HMF) can be recognized in full analogy with Hermite functions(HF), thus providing a unifying view to the theory of both HMF's and HF's. A few special cases of interest are also discussed.
A subgroup ![]() of a finite group
of a finite group ![]() is said to have the cover-avoidance property in
is said to have the cover-avoidance property in ![]() and is called a CAP-subgroup of
and is called a CAP-subgroup of ![]() if
if ![]() either covers or avoids each chief factor of
either covers or avoids each chief factor of ![]() . It is not difficult to show that the cover-avoidance property is neither persistent nor transitive, but various properties of CAP-subgroups can be obtained by considering weaker forms of persistence and transitivity. In particular, for a CAP-subgroup
. It is not difficult to show that the cover-avoidance property is neither persistent nor transitive, but various properties of CAP-subgroups can be obtained by considering weaker forms of persistence and transitivity. In particular, for a CAP-subgroup ![]() of
of ![]() , we say that
, we say that ![]() is CAP-transitive in
is CAP-transitive in ![]() if each CAP-subgroup of
if each CAP-subgroup of ![]() is a CAP-subgroup of
is a CAP-subgroup of ![]() , and we say that
, and we say that ![]() is CAP-persistent in
is CAP-persistent in ![]() if each CAP-subgroup of
if each CAP-subgroup of ![]() contained in
contained in ![]() is a CAP-subgroup of
is a CAP-subgroup of ![]() .
.
Let ![]() -groups,
-groups, ![]() -groups, and
-groups, and ![]() -groups be those groups in which, respectively, normality, permutability, and Sylow-permu-tability are transitive. We say
-groups be those groups in which, respectively, normality, permutability, and Sylow-permu-tability are transitive. We say ![]() is a
is a
![]() -group if
-group if ![]() is a
is a ![]() -group, while
-group, while ![]() is a Hall-
is a Hall-![]() group if
group if ![]() contains a normal nilpotent subgroup
contains a normal nilpotent subgroup ![]() such that
such that
![]() is an
is an ![]() -group. Some basic results on
-group. Some basic results on
![]() -groups, Hall-
-groups, Hall-![]() groups, Hall-
groups, Hall-![]() groups, and Hall-
groups, and Hall-![]() groups will be discussed along with some characterization theorems (in the finite solvable case). A key step in characterizing the above groups is showing that they have a nilpotent hypercommutator which is also a Hall subgroup. Also key is the result that
groups will be discussed along with some characterization theorems (in the finite solvable case). A key step in characterizing the above groups is showing that they have a nilpotent hypercommutator which is also a Hall subgroup. Also key is the result that ![]() being a
being a ![]() -group implies
-group implies ![]() is in fact a
is in fact a ![]() -group.
-group.
Preliminary report.
Generalizing a result for finite groups from Graham Ellis and Frank Leonard (1995) to polycylcic groups, we are able to apply both hand and computer methods to compute the nonabelian tensor square of the free nilpotent group of class 3 and rank ![]() . Using this approach we will also reproduce results from our paper on the nonabelian tensor square of 2-Engel groups of rank
. Using this approach we will also reproduce results from our paper on the nonabelian tensor square of 2-Engel groups of rank ![]() to appear in Proceedings of the Edinburgh Mathematical Society (joint work with Russell D. Blyth and Robert F. Morse).
to appear in Proceedings of the Edinburgh Mathematical Society (joint work with Russell D. Blyth and Robert F. Morse).
Fix any prime ![]() and positive integer
and positive integer ![]() . Let
. Let ![]() denote the cyclic group of order
denote the cyclic group of order ![]() . For each integer
. For each integer ![]() , define
, define ![]() to be the regular wreath product group
to be the regular wreath product group
![]() . We mention that
. We mention that ![]() is isomorphic to a Sylow
is isomorphic to a Sylow ![]() -subgroup of the symmetric group
-subgroup of the symmetric group ![]() , and that for each prime power
, and that for each prime power ![]() such that
such that ![]() is the full
is the full ![]() -part of
-part of ![]() , the group
, the group ![]() is isomorphic to a Sylow
is isomorphic to a Sylow ![]() -subgroup of
-subgroup of
![]() if and only if
if and only if ![]() .
.
We determine the ascending central series (and in the process, the nilpotence class) of ![]() , which has a very nice description. For
, which has a very nice description. For ![]() , its nilpotence class is
, its nilpotence class is
![]() . Using similar methods, we also determine the ascending central series and the nilpotence class of the regular wreath product group
. Using similar methods, we also determine the ascending central series and the nilpotence class of the regular wreath product group
![]() , where
, where ![]() is elementary abelian of order
is elementary abelian of order ![]() , for an arbitrary positive integer
, for an arbitrary positive integer ![]() . We determine that this last group has nilpotence class
. We determine that this last group has nilpotence class
![]() .
.
We will define a geometry on which an orthogonal group ![]() acts. We will show that this geometry is simply connected and using Tits' lemma we will be able to identify
acts. We will show that this geometry is simply connected and using Tits' lemma we will be able to identify ![]() with the universal completion of an interesting amalgam of its subgroups.
with the universal completion of an interesting amalgam of its subgroups.
Outer automorphism groups of fundamental groups of surfaces of genus ![]() are known to be residually finite. These groups can be considered either as generalized free products or 1-relator groups. It is natural to ask which generalized free products or 1-relator groups have residually finite outer automorphism groups. We prove certain generalized free products have Property
are known to be residually finite. These groups can be considered either as generalized free products or 1-relator groups. It is natural to ask which generalized free products or 1-relator groups have residually finite outer automorphism groups. We prove certain generalized free products have Property ![]() , from which we derived that certain tree products of groups have residually finite outer automorphism groups. We apply these results to groups of linkages, hose knots and 1-relator groups with non-trivial
centers (joint work with G. Kim).
, from which we derived that certain tree products of groups have residually finite outer automorphism groups. We apply these results to groups of linkages, hose knots and 1-relator groups with non-trivial
centers (joint work with G. Kim).
It is known that in a finite solvable group ![]() , a subgroup
, a subgroup ![]() is abnormal if and only if every subgroup of
is abnormal if and only if every subgroup of ![]() containing
containing ![]() is self-normalizing in
is self-normalizing in ![]() . Although, in general, the assumption of solvability cannot be dropped, in this talk we discuss a proof of the theorem for the special case
. Although, in general, the assumption of solvability cannot be dropped, in this talk we discuss a proof of the theorem for the special case ![]() and
and ![]() a second maximal intransitive subgroup of
a second maximal intransitive subgroup of ![]() . Qinhai Zhang has previously spoken on this topic at these meetings in the case where
. Qinhai Zhang has previously spoken on this topic at these meetings in the case where ![]() is a power of a prime (joint work with Ben Brewster, Binghamton University and Qinhai Zhang, Shanxi Teachers University).
is a power of a prime (joint work with Ben Brewster, Binghamton University and Qinhai Zhang, Shanxi Teachers University).
Professor Kappe has studied the power margin in groups. One goal of this research is to find conditions on groups which force the powers of elements to behave in an aesthetically pleasing way. For ![]() -groups, these three properties of regular
-groups, these three properties of regular ![]() -groups are generally considered desirable:
-groups are generally considered desirable:
Antonio Behn proved that if ![]() is prime
is prime ![]() ring with
ring with ![]() polycyclic-by-finite, then
polycyclic-by-finite, then ![]() is torsion-free or
is torsion-free or
![]() and
and
![]() . In this paper we prove that if
. In this paper we prove that if ![]() is semiprime
is semiprime ![]() ring
having no domains summands with
ring
having no domains summands with ![]() polycyclic-by-finite, then
polycyclic-by-finite, then ![]() is
hereditary. Description of such group algebra, when
is
hereditary. Description of such group algebra, when ![]() is algebraically
closed, is also given (JoinT work with S. K. Jain and J. B. Srivastava).
is algebraically
closed, is also given (JoinT work with S. K. Jain and J. B. Srivastava).
A right ![]() -module
-module ![]() is said to be subdirectly irreducible if it is nonzero and has a smallest nonzero submodule, or equivalently, if
is said to be subdirectly irreducible if it is nonzero and has a smallest nonzero submodule, or equivalently, if ![]() has a simple essential socle. Since this concept is dual to that of cyclic module, subdirectly irreducible modules are also called cocyclic. A submodule
has a simple essential socle. Since this concept is dual to that of cyclic module, subdirectly irreducible modules are also called cocyclic. A submodule ![]() of
of ![]() is said to be a subdirectly irreducible (or cococyclic) submodule of
is said to be a subdirectly irreducible (or cococyclic) submodule of ![]() if the quotient module
if the quotient module ![]() is subdirectly
irreducible. These concepts can be naturally relativized with respect to a hereditary torsion theory
is subdirectly
irreducible. These concepts can be naturally relativized with respect to a hereditary torsion theory ![]() on Mod-
on Mod-![]() , or more generally, can be defined for arbitrary posets with 0 and 1.
, or more generally, can be defined for arbitrary posets with 0 and 1.
As a module is the sum of all its cyclic modules, dually, for any module ![]() , the intersection of all subdirectly submodules of
, the intersection of all subdirectly submodules of ![]() is zero; one also says that the lattice of all submodules of
is zero; one also says that the lattice of all submodules of ![]() is rich in subdirectly irreducibles. The relative version of this property does not hold in general.
is rich in subdirectly irreducibles. The relative version of this property does not hold in general.
In this talk we characterize right modules ![]() having relative
having relative ![]() -dual Krull dimension less than or equal to a given ordinal. This requires that
-dual Krull dimension less than or equal to a given ordinal. This requires that ![]() is rich in
is rich in ![]() -subdirectly irreducibles. Therefore, we first look for sufficient conditions on the torsion theory
-subdirectly irreducibles. Therefore, we first look for sufficient conditions on the torsion theory ![]() to insure that, for any module
to insure that, for any module ![]() , the lattice of all
, the lattice of all ![]() -closed submodules of
-closed submodules of ![]() is rich in subdirectly irreducibles. In particular we give a relative version to an extension in the more general setting of dual Krull dimension of a nice recent result due to Carl Faith saying that a right
is rich in subdirectly irreducibles. In particular we give a relative version to an extension in the more general setting of dual Krull dimension of a nice recent result due to Carl Faith saying that a right ![]() -module
-module ![]() is Noetherian if and only if
is Noetherian if and only if ![]() is QFD and satisfies the ACC on subdirectly irreducible
submodules.
is QFD and satisfies the ACC on subdirectly irreducible
submodules.
The results to be presented, have been obtained jointly with Mihai Iosif (Bucharest University, Romania) and Mark L. Teply (University of Wisconsin-Milwaukee, USA).
A ring ![]() is called right (left) max-min
is called right (left) max-min ![]() -ring if every maximal closed
right (left) ideal with nonzero left (right) annihilator and every minimal
closed right (left) ideal of
-ring if every maximal closed
right (left) ideal with nonzero left (right) annihilator and every minimal
closed right (left) ideal of ![]() is a direct summand of
is a direct summand of ![]() . In this paper
we show that if
. In this paper
we show that if ![]() is a prime ring which is not a domain, then
is a prime ring which is not a domain, then ![]() is right
nonsingular, right max-min
is right
nonsingular, right max-min ![]() -ring with uniform right ideal if and only if
-ring with uniform right ideal if and only if
![]() is left nonsingular, left max-min
is left nonsingular, left max-min ![]() -ring with uniform left ideal. The
above result gives, in particular, Huynh-Jain-López Theorem [Proc. Amer.
Math. Soc. 128, 3153-3157 (2000)] (joint work with Adel N. Alahmadi and S. K. Jain).
-ring with uniform left ideal. The
above result gives, in particular, Huynh-Jain-López Theorem [Proc. Amer.
Math. Soc. 128, 3153-3157 (2000)] (joint work with Adel N. Alahmadi and S. K. Jain).
(Preliminary report)
We investigate modules which satisfy an analog in ![]() of the "condition H" introduced in Gabriel's thesis.
of the "condition H" introduced in Gabriel's thesis.
Fifteen years ago, Bell and Guerriero conjectured that a ring having only a finite number of noncentral subrings must be either finite or commutative. We have recently found a proof of this result, which involves some unexpected notions. We give an indication of the proof, and we discuss some related results.
(This talk is based on joint work with Jae Keol Park and S. Tariq Rizvi).
In this talk we discuss various concepts for the hull of a ring or module, where the hull is from a certain class of rings or modules, respectively. Existence and/or uniqueness results on hulls from various classes (including extending, FI-extending, continuous, Baer, etc.) are presented. Also the transfer of information between an object and its hull is considered. Examples are provided to illustrate the theory.
We consider conditions that make the rings in the title Noetherian.
A type decomposition of a module ![]() over a ring
over a ring ![]() is a direct sum
decomposition for which any two distinct summands have no nonzero
isomorphic submodules. In this paper, we investigate when a module
possesses certain kinds of type decompositions and when such
decompositions are unique.
is a direct sum
decomposition for which any two distinct summands have no nonzero
isomorphic submodules. In this paper, we investigate when a module
possesses certain kinds of type decompositions and when such
decompositions are unique.
A class of right ![]() -modules
-modules
![]() of modules is a type (or natural
class) if it is closed under isomorphic copies, submodules, arbitrary
direct sums and injective hulls. A submodule
of modules is a type (or natural
class) if it is closed under isomorphic copies, submodules, arbitrary
direct sums and injective hulls. A submodule ![]() of
of ![]() is a
type submodule if, for some type
is a
type submodule if, for some type
![]() ,
, ![]() is a submodule
of
is a submodule
of ![]() which is maximal with respect to
which is maximal with respect to
![]() . In this case,
we also say
. In this case,
we also say ![]() is a type submodule of type
is a type submodule of type
![]() .
Just as every submodule
.
Just as every submodule ![]() has a complement closure in
has a complement closure in ![]() , so also it has a
type closure
, so also it has a
type closure
![]() . Just as in the complement case,
. Just as in the complement case,
![]() need not be unique. A module
need not be unique. A module ![]() satisfies UTC (unique type closure) if
every submodule
satisfies UTC (unique type closure) if
every submodule ![]() has a unique type closure
has a unique type closure
![]() , or equivalently
if for every type
, or equivalently
if for every type
![]() ,
, ![]() has a unique type submodule of type
has a unique type submodule of type
![]() .
Several equivalent characterizations of UTC modules are obtained.
Fully invariant type submodules and fully invariant type direct summands are explored.
.
Several equivalent characterizations of UTC modules are obtained.
Fully invariant type submodules and fully invariant type direct summands are explored.
Galois rings have been used widely in Algebraic Coding Theory.
In this talk, we will discuss negacyclic codes of length ![]() over Galois
rings. It will be shown that
over Galois
rings. It will be shown that
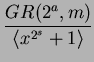 is indeed a chain ring, and hence obtaining the complete
structure of negacyclic codes of length
is indeed a chain ring, and hence obtaining the complete
structure of negacyclic codes of length ![]() over
over
![]() , as well
as that of their duals. We also address the minimum Hamming weights of
such negacyclic codes. Open directions for further investigations will
also be discussed.
, as well
as that of their duals. We also address the minimum Hamming weights of
such negacyclic codes. Open directions for further investigations will
also be discussed.
A right module ![]() over a ring
over a ring ![]() (with identity) is called endofinite if it has finite length as a left module over its endomorphism ring. It is well-known that endofinite modules have many attractive properties: Every endofinite module
(with identity) is called endofinite if it has finite length as a left module over its endomorphism ring. It is well-known that endofinite modules have many attractive properties: Every endofinite module ![]() is
is ![]() -pure-injective, with nilpotent Jacobson radical of the endomorphism ring End
-pure-injective, with nilpotent Jacobson radical of the endomorphism ring End![]() , and admits an indecomposable decomposition
, and admits an indecomposable decomposition
![]() , where the number of isomorphism classes of the
, where the number of isomorphism classes of the ![]() is finite. In this talk, we will discuss modules satisfying some weaker forms of chain conditions on endosubmodules, and show that a number of the above properties of endofinite modules can be extended to our situation. Among the applications, we show that any pure-injective pure-projective module over an Artin algebra is endo-Artinian. (A part of the results of this talk is based on our joint work with Sergio R. López-Permouth).
is finite. In this talk, we will discuss modules satisfying some weaker forms of chain conditions on endosubmodules, and show that a number of the above properties of endofinite modules can be extended to our situation. Among the applications, we show that any pure-injective pure-projective module over an Artin algebra is endo-Artinian. (A part of the results of this talk is based on our joint work with Sergio R. López-Permouth).
It is proved that a ring ![]() is right
is right ![]() -pure injective in the
category of flat modules if and only if it is right perfect. Several other
conditions are shown to be equivalent. For example, that a countable direct
sum of copies of its pure-injective envelope in Flat-
-pure injective in the
category of flat modules if and only if it is right perfect. Several other
conditions are shown to be equivalent. For example, that a countable direct
sum of copies of its pure-injective envelope in Flat-![]() is pure-injective in
that category. (Joint work with Ivo Herzog).
is pure-injective in
that category. (Joint work with Ivo Herzog).
Many arguments in the Theory of Rings and Module are, on close inspection, purely Lattice theoretic arguments. Grigore Calugareanu has a long repertoire of such results in his book "Lattice Concepts on Module Theory". The Levitski-Hopkins Theorem is interesting from this point of view, because only part of it lends to an obvious lattice theory approach. The rest of it requires a new construction, the Hyper-radical, which will be presented in this talk.
It is shown that a ring is right cotorsion if and only if it is the endomorphism ring of a pure-injective object in a locally finitely presented additive category. It is also shown that these rings are (von Neumann) regular and self injective module their Jacobson radical and idempotents lift. (Joint work with Pedro A. Guil Asensio).
A ring ![]() is said to be right CS if every right ideal is essential in a summand
of
is said to be right CS if every right ideal is essential in a summand
of ![]() . A right CS ring is said to be right continuous if any right ideal of
. A right CS ring is said to be right continuous if any right ideal of ![]() which is isomorphic to a summand of
which is isomorphic to a summand of ![]() is itself a summand of
is itself a summand of ![]() . Right
CS rings and right continuous rings are generalizations of right selfinjective
rings. It is known that the group algebra
. Right
CS rings and right continuous rings are generalizations of right selfinjective
rings. It is known that the group algebra ![]() of a group
of a group ![]() over a field
over a field ![]() is selfinjective if and only if
is selfinjective if and only if ![]() is a finite group. The group algebra
is a finite group. The group algebra ![]() is
principally injective if and only if
is
principally injective if and only if ![]() is a locally finite group. We discuss group
algebras that are continuous (or CS) and give the corresponding conditions
on the group
is a locally finite group. We discuss group
algebras that are continuous (or CS) and give the corresponding conditions
on the group ![]() . Among others, it is shown that if the group algebra
. Among others, it is shown that if the group algebra ![]() of
a group
of
a group ![]() over a field
over a field ![]() is right continuous then
is right continuous then ![]() is a locally finite group.
In particular, a right continuous group algebra is principally injective.
is a locally finite group.
In particular, a right continuous group algebra is principally injective.
We investigate in this paper von Neumann regularity of certain rings whose simple singular left ![]() -modules are
-modules are ![]() -injective. As a nontrivial generalization of a reflexive ring, idempotent reflexive ring is considered. It is proved that if
-injective. As a nontrivial generalization of a reflexive ring, idempotent reflexive ring is considered. It is proved that if ![]() is an idempotent reflexive ring whose simple singular left
is an idempotent reflexive ring whose simple singular left ![]() -modules are
-modules are ![]() -injective, then for any nonzero element
-injective, then for any nonzero element ![]() in
in ![]() , there exists a positive integer
, there exists a positive integer ![]() such that
such that ![]() and
and
![]() . Several known results are extended and unified.
. Several known results are extended and unified.
In joint work with L. Levy, we showed that a commutative,
Noetherian ring ![]() has tame representation type if and only if
has tame representation type if and only if ![]() is a
Klein ring or a homomorphic image of a Dedekind-like ring.
is a
Klein ring or a homomorphic image of a Dedekind-like ring.
Klein rings have finite length, while Dedekind-like rings are reduced and
one-dimensional and have the property that all of their finitely generated
indecomposable modules have torsion-free rank at most two. Following this
observation, R. Wiegand conjectured that, for a commutative, Noetherian,
reduced, one-dimensional ring ![]() , there is a bound on the torsion-free
rank of finitely generated indecomposable
, there is a bound on the torsion-free
rank of finitely generated indecomposable ![]() -modules if and only if
-modules if and only if ![]() has tame representation type (if and only if
has tame representation type (if and only if ![]() is a Dedekind-like ring).
is a Dedekind-like ring).
In joint work with W. Hassler, R. Karr, and R. Wiegand, we prove this conjecture and more.
We say a ring is "right annelidan" if the right annihilator of any element of the ring is a right waist. This class of rings encompasses domains as well as right uniserial rings and certain other local rings. We obtain results on the structure of right annelidan rings, their ideals, and important radicals. We show the Köthe Conjecture holds for this class of rings, and we study the relationship between this and various other major classes of rings (joint work with Ryszard Mazurek).
We discuss a right injective hull ![]() of a ring
of a ring ![]() such that
such that ![]() has exactly four distinct
ring structures whose multiplications extend the module multiplication of
has exactly four distinct
ring structures whose multiplications extend the module multiplication of ![]() over
over ![]() and all
these ring structures are isomorphic. This gives a negative answer to Osofsky’s question on
the uniqueness of the compatible ring multiplication for the injective hull. Various types
of ring hulls of
and all
these ring structures are isomorphic. This gives a negative answer to Osofsky’s question on
the uniqueness of the compatible ring multiplication for the injective hull. Various types
of ring hulls of ![]() and all intermediate ring structures between
and all intermediate ring structures between ![]() and
and ![]() are discussed.
(jointly done with Gary F. Birkenmeier and S. Tariq Rizvi).
are discussed.
(jointly done with Gary F. Birkenmeier and S. Tariq Rizvi).
We discuss old and prove new results on rings over which every projective right module is a direct sum of finitely generated modules.
By Albrecht and Bass this is true for left or right semihereditary rings. It follows from a generalization of Krull-Azumaya-Schmidt theorem that semiperfect rings enjoy this property. By Harada the same is true for every commutative weakly noetherian ring.
We give a precise criterion (in terms of matrices over a ring) when every projective right module is a direct sum of finitely generated modules.
Outside the above mentioned classes of rings, the answer to this question is widely unknown. For instance, it is not known if every projective module over a commutative domain is a direct sum of finitely generated modules.
In particular, we give different examples of noetherian rings where the answer to the above question is 1) negative; 2) positive; and 3) unknown.
For instance, as a byproduct of our results we give
a complete classification of non-finitely generated projective
modules over all primitive factors of ![]() (
(![]() is an
algebraically closed field of characteristic zero) and over the
ring of differential operators on
is an
algebraically closed field of characteristic zero) and over the
ring of differential operators on
![]() , the
projective space.
, the
projective space.
The following statement is known as Vaught's conjecture:
Conjecture. Let ![]() be a countable complete first-order theory. If
be a countable complete first-order theory. If ![]() has uncountably many non-isomorphic countable models, then
has uncountably many non-isomorphic countable models, then ![]() has
has
![]() non-isomorphic countable models.
non-isomorphic countable models.
Garavaglia proved Vaught's conjecture for ![]() -stable theories of modules in 1980. In 1984 Shelah extended this result to arbitrary
-stable theories of modules in 1980. In 1984 Shelah extended this result to arbitrary ![]() -stable theories.
-stable theories.
The main objective of this talk is to show that Vaught's conjecture is true for any complete theory ![]() of modules over 1) countable serial rings; 2) countable commutative Prüfer rings; 3) countable hereditary noetherian prime rings and 4) tame hereditary finite-dimensional algebras over a countable infinite field. In all these cases we prove that, if
of modules over 1) countable serial rings; 2) countable commutative Prüfer rings; 3) countable hereditary noetherian prime rings and 4) tame hereditary finite-dimensional algebras over a countable infinite field. In all these cases we prove that, if ![]() has few types, then it is
has few types, then it is ![]() -stable, making it possible to apply Garavaglia's result.
-stable, making it possible to apply Garavaglia's result.
We give a complete classification of modules with few models over countable serial rings, and of modules with few types over countable commutative Prüfer rings. A similar description holds true for modules over a string algebra
![]() over a finite or countable field
over a finite or countable field ![]() .
.
We also discuss some partial results on Vaught's conjecture for modules over group rings and for modules over pullback rings.
Recently we defined the concept of right Baer modules over a ring ![]() . A module
. A module ![]() is called Baer if the right annihilator of any set of endomorphisms of
is called Baer if the right annihilator of any set of endomorphisms of ![]() , in
, in ![]() is a direct summand of
is a direct summand of ![]() . This concept generalizes the concept of Baer rings. Kaplansky developed a theory of types for Baer rings, and Goodearl and Boyle extended it to nonsingular injective modules. We extend this type theory to Baer modules and, in particular, since nonsingular CS modules are Baer, to nonsingular CS modules (joint work with S.T. Rizvi).
. This concept generalizes the concept of Baer rings. Kaplansky developed a theory of types for Baer rings, and Goodearl and Boyle extended it to nonsingular injective modules. We extend this type theory to Baer modules and, in particular, since nonsingular CS modules are Baer, to nonsingular CS modules (joint work with S.T. Rizvi).
A ring ![]() is called a right Harada ring if it is right Artinian and every non-small right
is called a right Harada ring if it is right Artinian and every non-small right ![]() -module contains a non-zero injective submodule. The first result in our report is the following Theorem:
Let
-module contains a non-zero injective submodule. The first result in our report is the following Theorem:
Let ![]() be a right perfect ring. Then
be a right perfect ring. Then ![]() is a right Harada ring if and only if every cyclic module
is a direct sum of an injective module and a small module; if and only if every localmodule is either injective or small. We also prove that a ring
is a right Harada ring if and only if every cyclic module
is a direct sum of an injective module and a small module; if and only if every localmodule is either injective or small. We also prove that a ring ![]() is QF if and only if every cyclic module is a direct sum of a
projective injective module and a small module; if and only if every local module is either projective
injective or small. Finally, a right QF-3 right perfect ring
is QF if and only if every cyclic module is a direct sum of a
projective injective module and a small module; if and only if every local module is either projective
injective or small. Finally, a right QF-3 right perfect ring ![]() is serial if and only if every right ideal is a direct sum of a projective module and a singular module.
is serial if and only if every right ideal is a direct sum of a projective module and a singular module.
For ![]() an algebra, consider the category
an algebra, consider the category ![]() of all pairs
of all pairs
![]() where
where ![]() is a finite length
is a finite length ![]() -module and
-module and ![]() a submodule of
a submodule of ![]() .
Then
.
Then ![]() is a full and exact subcategory of a module category, so
every object in
is a full and exact subcategory of a module category, so
every object in ![]() is a direct sum of indecomposables. It
turns out that
is a direct sum of indecomposables. It
turns out that ![]() has Auslander-Reiten sequences, so we computed a
formula for the Auslander-Reiten translation, which acts on the set of
indecomposables in
has Auslander-Reiten sequences, so we computed a
formula for the Auslander-Reiten translation, which acts on the set of
indecomposables in ![]() . Surprisingly, for
. Surprisingly, for ![]() a uniserial ring,
this translation has period six. This is a report on joint work with
Claus Michael Ringel.
a uniserial ring,
this translation has period six. This is a report on joint work with
Claus Michael Ringel.
(Joint work with Lianyond Xue)
Let ![]() be a Galois algebra over a commutative ring
be a Galois algebra over a commutative ring ![]() with Galois
group
with Galois
group ![]() . Then
. Then ![]() is a direct sum of Galois algebras such that each direct
summand is a composition of a central Galois algebra and a commutative
Galois algebra. A sufficient condition is also given under which
is a direct sum of Galois algebras such that each direct
summand is a composition of a central Galois algebra and a commutative
Galois algebra. A sufficient condition is also given under which ![]() is
commutative.
is
commutative.