Group Theory Abstracts
Groups in which the hypercentral factor group is a 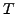 - group
- group
James C. Beidleman
Basic properties of the class mentioned in the title will
be presented. Let 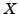 be the nonabelian
group of order
be the nonabelian
group of order 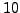 and
and 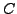 be the cyclic group of order
be the cyclic group of order 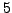 .
Put
.
Put
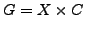 and note that
and note that  is not a
is not a 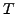 -group but is in
the class mentioned in the title.
This example will motivate some of our results.
-group but is in
the class mentioned in the title.
This example will motivate some of our results.
DEPARTMENT OF MATHEMATICS
UNIVERSITY OF KENTUCKY
LEXINGTON, KY 40506-0027
clark at ms.uky.edu
+++++++++++++++++++++++++++++++++++++++
Note on
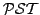 -groups
-groups
Matthew Ragland
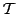 -groups are the
groups in which normality is transitive.
One can generalize the concept of a
-groups are the
groups in which normality is transitive.
One can generalize the concept of a
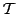 -group by requiring
Sylow-permutability to be transitive. We call
-group by requiring
Sylow-permutability to be transitive. We call  a
a
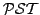 -group if
whenever
-group if
whenever 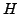 permutes with the Sylow subgroups of
permutes with the Sylow subgroups of 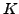 and
and 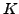 permutes with
the Sylow subgroups of
permutes with
the Sylow subgroups of  we have
we have 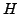 permutes with the Sylow subgroups of
permutes with the Sylow subgroups of
 . Let us say
. Let us say  satisfies the property
satisfies the property
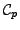 if every subgroup
of a Sylow
if every subgroup
of a Sylow
 -subgroup
-subgroup 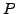 of
of  is normal in
is normal in 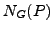 . Also, let us
say
. Also, let us
say  satisfies the property
satisfies the property
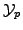 if for every Sylow
if for every Sylow  -subgroup
-subgroup
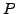 of
of  we have
we have
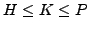 implies
implies 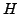 permutes with the Sylow
subgroups of
permutes with the Sylow
subgroups of 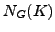 .
M. Asaad has shown in a recent paper that
.
M. Asaad has shown in a recent paper that  is a solvable
is a solvable
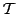 -group
if and only if
-group
if and only if  satisfies the property
satisfies the property
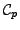 for all primes
for all primes  dividing the order of
dividing the order of 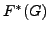 , the generalized Fitting subgroup of
, the generalized Fitting subgroup of  .
We wish to discuss a proof for the following theorem:
.
We wish to discuss a proof for the following theorem:
Theorem 1
 is a solvable
is a solvable
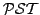 -group
if and only if
-group
if and only if  satisfies the property
satisfies the property
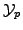 for all primes
for all primes  dividing the order of
dividing the order of 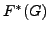 .
.
This is joint work with Adolfo Ballester-Bolinches and Ramon
Esteban-Romero.
DEPARTMENT OF MATHEMATICS
AUBURN UNIVERSITY MONTGOMERY
3348 WALTON DR.
MONTGOMERY AL 36111
mragland at mail.aum.edu
+++++++++++++++++++++++++++++++++++++++
Transitive and Persistent Subgroups
Joseph Petrillo
Given subgroup properties 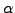 and
and 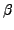 ,
a subgroup
,
a subgroup 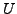 of a group
of a group  may or may not possess one or
both of the following properties:
may or may not possess one or
both of the following properties:
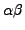 -transitivity:
Every
-transitivity:
Every 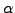 -subgroup of
-subgroup of 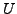 is a
is a 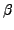 -subgroup of
-subgroup of  .
.
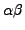 -persistence:
Every
-persistence:
Every 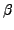 -subgroup of
-subgroup of  in
in 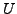 is an
is an 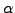 -subgroup of
-subgroup of 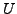 .
.
We will present some elementary results and discuss examples of
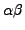 -transitive and
-transitive and
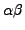 -persistent subgroups.
-persistent subgroups.
ALFRED UNIVERSITY
SAXON DRIVE
ALFRED, NY 14802
petrillo at alfred.edu
+++++++++++++++++++++++++++++++++++++++
Extremely primitive groups
Ákos Seress
Joint work with Avinoam Mann and Cheryl Praeger
A finite primitive permutation group  is extremely primitive if a point
stabiliser
is extremely primitive if a point
stabiliser 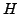 is primitive on each of its orbits. Cyclic groups of prime
order, and doubly primitive groups provide infinite families of
examples. Efforts to classify the remaining examples (non-regular,
simply primitive) are the subject of the lecture.
A result of W. A. Manning from 1927
tells us that the stabiliser H acts faithfully on each of its
non-trivial orbits. Thus we have an embedding of a primitive group
is primitive on each of its orbits. Cyclic groups of prime
order, and doubly primitive groups provide infinite families of
examples. Efforts to classify the remaining examples (non-regular,
simply primitive) are the subject of the lecture.
A result of W. A. Manning from 1927
tells us that the stabiliser H acts faithfully on each of its
non-trivial orbits. Thus we have an embedding of a primitive group 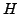 (or, rather, several primitive actions of
(or, rather, several primitive actions of 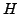 ) in a larger primitive group
) in a larger primitive group
 . Specific examples of this embedding problem led to the construction
of several of the sporadic simple groups, and indeed sporadic groups
provide interesting examples of extremely primitive groups. The
classification divides into two cases - almost simple and affine - each
of which contributes interesting lists of examples. Our aim is to prove
that our lists are complete up to a finite number of exceptions. We have
achieved this in the affine case; the specificity of our results depends
on the strength of asymptotic bounds on the number of maximal subgroups
of almost simple groups.
. Specific examples of this embedding problem led to the construction
of several of the sporadic simple groups, and indeed sporadic groups
provide interesting examples of extremely primitive groups. The
classification divides into two cases - almost simple and affine - each
of which contributes interesting lists of examples. Our aim is to prove
that our lists are complete up to a finite number of exceptions. We have
achieved this in the affine case; the specificity of our results depends
on the strength of asymptotic bounds on the number of maximal subgroups
of almost simple groups.
THE OHIO STATE UNIVERSITY
COLUMBUS, OH 43210
akos at math.ohio-state.edu
+++++++++++++++++++++++++++++++++++++++
Four-variable associative laws for group commutators
Fernando Guzman
In 1941 F. W. Levi proved that a group is nilpotent of class
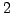 if and only if the commutator operation is associative.
Recently, Geoghegan and Guzman showed that a group is
solvable if and only if the commutator operation eventually satisfies
all instances of the generalized
associative law.
In this talk we discuss solvability and nilpotency
of groups whose commutator operation satisfies one of the
four-variable instances of the associative law.
if and only if the commutator operation is associative.
Recently, Geoghegan and Guzman showed that a group is
solvable if and only if the commutator operation eventually satisfies
all instances of the generalized
associative law.
In this talk we discuss solvability and nilpotency
of groups whose commutator operation satisfies one of the
four-variable instances of the associative law.
DEPARTMENT OF MATHEMATICAL SCIENCES
BINGHAMTON UNIVERSITY
BINGHAMTON, NY. 13902-6000
fer at math.binghamton.edu
+++++++++++++++++++++++++++++++++++++++
R. Thompson's group 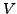 from a dynamical viewpoint
from a dynamical viewpoint
Olga Patricia Salazar-Diaz
An element of Thompson's group 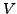 can be defined as an automorphism
of a certain algebra or as a self homeomorphism of the Cantor set.
Thus, the dynamics of an element of
can be defined as an automorphism
of a certain algebra or as a self homeomorphism of the Cantor set.
Thus, the dynamics of an element of 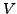 can be studied.
We analize the dynamics and use the analysis to give another
solution of the conjugacy problem in
can be studied.
We analize the dynamics and use the analysis to give another
solution of the conjugacy problem in 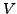 .
.
DEPARTMENT OF MATHEMATICAL SCIENCES
BINGHAMTON UNIVERSITY
BINGHAMTON, NY. 13902-6000
salazar at math.binghamton.edu
+++++++++++++++++++++++++++++++++++++++
Jordan Decomposition in Integral Group Rings
Lawrence E. Wilson
The Jordan Decomposition is related to writing the Jordan Normal
Form of a matrix as the sum of a diagonal matrix and an upper-triangular
matrix. Similarly, if the matrix is invertible, you can write it as a
product of a diagonal matrix and a unipotent matrix. One can ask whether
for integral matrices these two summands (or products) also have integer
entries. This question is well-understood for matrices and has been
investigated for elements of integer group rings. My co-authors and I
have found the complete answer for 2-groups and made important advances
when the group order is divisible by a prime at least 5.
CENTER FOR COMMUNICATIONS RESEARCH
4320 WESTERRA CT
SAN DIEGO, CA 92121
larry at ccrwest.org
+++++++++++++++++++++++++++++++++++++++
Fusion systems of blocks of group algebras
Radu Stancu
Fix  a prime number. Fusion systems on finite
a prime number. Fusion systems on finite  -groups were
introduced by L. Puig
and provide an axiomatic framework for studying the
-groups were
introduced by L. Puig
and provide an axiomatic framework for studying the  -local structure
(also called
-local structure
(also called  -fusion)
in finite groups. The p-local structure of a finite group
-fusion)
in finite groups. The p-local structure of a finite group  is given by the
conjugation with elements of
is given by the
conjugation with elements of  between the
subgroups of a Sylow
between the
subgroups of a Sylow  -subgroup of
-subgroup of  . This axiomatic view point has
been very
useful in determining many properties of finite
groups and of the
. This axiomatic view point has
been very
useful in determining many properties of finite
groups and of the  -completion of their classifying spaces as well as in
modular
representation theory and it underlies the theory of
-completion of their classifying spaces as well as in
modular
representation theory and it underlies the theory of  -local finite groups
developed by C. Broto, R. Levi and B. Oliver.
-local finite groups
developed by C. Broto, R. Levi and B. Oliver.
So, the  -local structure of a finite group gives a fusion system. But
there are examples
of fusion systems that do not occur in this way. We call these examples
exotic fusion systems.
Let
-local structure of a finite group gives a fusion system. But
there are examples
of fusion systems that do not occur in this way. We call these examples
exotic fusion systems.
Let 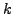 be an algebraically closed field of characteristic
be an algebraically closed field of characteristic  and
and  a
finite group.
An interesting question for fusion systems is whether they can be obtained
from the local
structure of a block of the group algebra
a
finite group.
An interesting question for fusion systems is whether they can be obtained
from the local
structure of a block of the group algebra 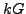 . In this talk I present a
joint work with Radha Kessar on some methods to reduce this question to
the case when
. In this talk I present a
joint work with Radha Kessar on some methods to reduce this question to
the case when  is a
central
is a
central 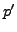 -extension of a simple group. As an application of our result,
we obtain that
the exotic fusion systems discovered by A. Ruiz and A. Viruel do not occur
as fusion systems of
-extension of a simple group. As an application of our result,
we obtain that
the exotic fusion systems discovered by A. Ruiz and A. Viruel do not occur
as fusion systems of  -blocks of finite groups.
-blocks of finite groups.
THE OHIO STATE UNIVERSITY
COLUMBUS, OH 43210
stancu at math.ohio-state.edu
+++++++++++++++++++++++++++++++++++++++
Products of commutators are not always commutators: Cassidy's example revisited
Luise-Charlotte Kappe
In her 1979 paper, entitled ``Products of commutators are not always
commutators: an example", P. J. Cassidy presents a group in which
the set of commutators is not equal to the commutator subgroup
(Monthly, vol. 86, p. 772). However, a typographical error in
Cassidy's paper impacts the verification of the claim.
In this talk we give a corrected proof of Cassidy's claim in a
slightly more general setting and take another look at her
example in context with the function
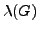 for a group
for a group  .
.
For a group  the function
the function
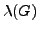 denotes the smallest
integer
denotes the smallest
integer 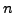 such that every element of the commutator subgroup
such that every element of the commutator subgroup  is a product of
is a product of 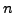 commutators. The statement that the set of
commutators of a group
commutators. The statement that the set of
commutators of a group  does not form a subgroup is equivalent
to
does not form a subgroup is equivalent
to
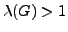 . For every prime
. For every prime  , Guralnick has constructed
a
, Guralnick has constructed
a  -group
-group 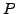 of order
of order 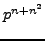 with
with
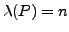 .
For Cassidy's group
.
For Cassidy's group 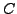 we have
we have
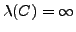 .
However for given
.
However for given 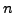 and any prime
and any prime  , the group
, the group 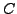 has a suitable homomorphic image
has a suitable homomorphic image
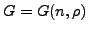 such
that
such
that
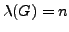 and
and  has order
has order
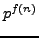 , where
, where 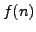 is a linear function in
is a linear function in 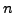 .
.
DEPARTMENT OF MATHEMATICAL SCIENCES
BINGHAMTON UNIVERSITY
BINGHAMTON, NY. 13902-6000
menger at math.binghamton.edu
+++++++++++++++++++++++++++++++++++++++
For a given prime  , what is the smallest nonabelian group whose order is divisible by
, what is the smallest nonabelian group whose order is divisible by  ?
?
Gabriela A. Mendoza
In this talk we will show that for any prime 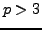 ,
,
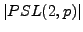 with order
with order
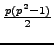 is the smallest nonabelian
simple group whose order is divisible by
is the smallest nonabelian
simple group whose order is divisible by  . For
. For 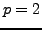 and
and 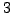 the
group in question is
the
group in question is 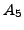 , the alternating group on
, the alternating group on 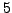 letters.
letters.
This answers a question posed at the Zassenhaus Conference 2005. It also strengthens the following result presented at the conference:
Theorem 2
Let  be a prime and let
be a prime and let 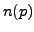 denote the order of the smallest group in which the elements of order dividing
denote the order of the smallest group in which the elements of order dividing  do not form a subgroup.
Then
do not form a subgroup.
Then
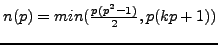 where
where
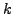 is the smallest integer for which
is the smallest integer for which 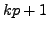 is a prime power.
is a prime power.
In our earlier result 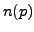 was defined only as
was defined only as
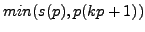 ,
where
,
where 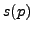 is the order of the smallest simple group in which the
elements of order
is the order of the smallest simple group in which the
elements of order  do not form a subgroup.
do not form a subgroup.
DEPARTMENT OF MATHEMATICAL SCIENCES
BINGHAMTON UNIVERSITY
BINGHAMTON, NY. 13902-6000
mendoza at math.binghamton.edu
+++++++++++++++++++++++++++++++++++++++
Nonsolvable Groups Satisfying the One-Prime Hypothesis (Part 1)
Donald L. White
(Joint work with Mark L. Lewis)
We say that a finite group  satisfies the
one-prime hypothesis if the greatest common
divisor of every pair of distinct ordinary
irreducible character degrees is either
satisfies the
one-prime hypothesis if the greatest common
divisor of every pair of distinct ordinary
irreducible character degrees is either 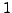 or a
prime. In earlier work, Lewis was able to prove a
bound on the number of character degrees for a
solvable group
or a
prime. In earlier work, Lewis was able to prove a
bound on the number of character degrees for a
solvable group  satisfying the one-prime
hypothesis and to show that the bound is best
possible.
satisfying the one-prime
hypothesis and to show that the bound is best
possible.
The aim of this paper is to classify the
nonsolvable groups satisfying the one-prime
hypothesis and to bound the number of character
degrees for such groups. In the first part, we
determine all almost simple groups, i.e., groups
 satisfying
satisfying
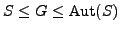 for a
nonabelian simple group
for a
nonabelian simple group 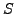 , satisfying the
one-prime hypothesis. In particular, we show that
, satisfying the
one-prime hypothesis. In particular, we show that
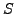 must be one of
must be one of 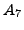 , the Suzuki group
, the Suzuki group
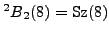 , or
, or
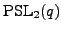 with
with 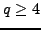 a power of a prime.
a power of a prime.
DEPARTMENT OF MATHEMATICAL SCIENCES
KENT STATE UNIVERSITY
KENT, OH 44242
white at math.kent.edu
+++++++++++++++++++++++++++++++++++++++
Nonsolvable Groups Satisfying the One-Prime Hypothesis (Part 2)
Mark L. Lewis
(This is joint work with Don White.)
Let  be a finite group, and let
be a finite group, and let
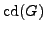 be the set of
irreducible character degrees
of
be the set of
irreducible character degrees
of  .
We say that
.
We say that  satisfies the One-prime hypothesis
if whenever
satisfies the One-prime hypothesis
if whenever
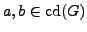 and
and 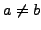 , then the greatest common
divisor of
, then the greatest common
divisor of 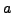 and
and 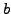 is either
is either 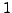 or a prime.
In an earlier series of papers, I showed that if
or a prime.
In an earlier series of papers, I showed that if  is
solvable and satisfies the one-prime
hypothesis, then
is
solvable and satisfies the one-prime
hypothesis, then
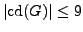 , and
I gave examples of solvable groups satisfying the one-prime
hypothesis where the bound is met. In
this talk, I will show that if
, and
I gave examples of solvable groups satisfying the one-prime
hypothesis where the bound is met. In
this talk, I will show that if  is a nonsolvable group
satisfying the one-prime hypothesis, then
is a nonsolvable group
satisfying the one-prime hypothesis, then
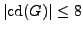 .
In particular, I will show how classifying the almost simple
groups that satisfy the one-prime
hypothesis can be used to classify the nonsolvable groups
that satisfy the one-prime hypothesis.
.
In particular, I will show how classifying the almost simple
groups that satisfy the one-prime
hypothesis can be used to classify the nonsolvable groups
that satisfy the one-prime hypothesis.
DEPARTMENT OF MATHEMATICAL SCIENCES
KENT STATE UNIVERSITY
KENT, OH 44242
lewis at math.kent.edu
+++++++++++++++++++++++++++++++++++++++
Bounds on the number of lifts of a Brauer character of a solvable group
James Patrick Cossey
The Fong-Swan Theorem guarantees that every Brauer character of a
solvable group  necessarily has a lift (i.e. an ordinary irreducible
character whose restriction to
necessarily has a lift (i.e. an ordinary irreducible
character whose restriction to  -regular elements is that Brauer character).
In this talk we will demonstrate methods for generating many such lifts,
and we will show upper and lower bounds on the number of lifts of a
Brauer character in terms of the nucleus and vertex of the character,
which are certain subgroups of
-regular elements is that Brauer character).
In this talk we will demonstrate methods for generating many such lifts,
and we will show upper and lower bounds on the number of lifts of a
Brauer character in terms of the nucleus and vertex of the character,
which are certain subgroups of  determined (up to conjugacy) by the
Brauer character.
determined (up to conjugacy) by the
Brauer character.
UNIVERSITY OF ARIZONA
6001 E PIMA ST APT 83
cossey at math.arizona.edu
+++++++++++++++++++++++++++++++++++++++
Orders of elements of subgroups of wreath product  -groups
-groups
Jeffrey M. Riedl
A finite group having a unique minimal normal subgroup is said to be
monolithic. Given a prime  and positive integers
and positive integers 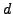 and
and 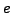 ,
we seek to classify up to isomorphism all the monolithic subgroups
of the regular wreath product group
,
we seek to classify up to isomorphism all the monolithic subgroups
of the regular wreath product group
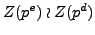 .
(This has already been done in case
.
(This has already been done in case 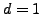 .)
In order to recognize when two such subgroups are not isomorphic
to each other, efficient methods are needed for calculating
isomorphism invariants (such as nilpotence class, order of the center)
for each in this vast collection of subgroups. For this purpose,
we have determined a general yet reasonably practical method for
counting the number of elements of each order in each of these subgroups.
.)
In order to recognize when two such subgroups are not isomorphic
to each other, efficient methods are needed for calculating
isomorphism invariants (such as nilpotence class, order of the center)
for each in this vast collection of subgroups. For this purpose,
we have determined a general yet reasonably practical method for
counting the number of elements of each order in each of these subgroups.
UNIVERSITY OF AKRON
250 BUCHTEL COMMON
AKRON, OH 44325-4002
riedl at uakron.edu
+++++++++++++++++++++++++++++++++++++++
Inductive arguments for the non-coprime 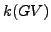 -problem
-problem
Thomas Michael Keller
The non-coprime 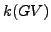 -problem deals with the general question of
how the number of conjugacy classes of the semidirect product
-problem deals with the general question of
how the number of conjugacy classes of the semidirect product 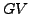 is bounded in terms of the cardinality of
is bounded in terms of the cardinality of 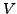 , where
, where  is a
finite group and
is a
finite group and 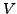 is a finite faithful
is a finite faithful  -module.
We present some arguments that may be useful in an inductive approach
to this problem.
-module.
We present some arguments that may be useful in an inductive approach
to this problem.
TEXAS STATE UNIVERSITY
601 UNIVERSITY DRIVE
SAN MARCOS, TX 78666
keller at txstate.edu
+++++++++++++++++++++++++++++++++++++++
Groups Whose Normalizers Form a Lattice
Joseph Patrick Smith
I will examine groups whose norm is a normalizer within the group.
I will start be showing that these groups are nilpotent, which
reduces the problem to the realm of  -groups.
I will proceed to show that any group that contains the norm is also
a normalizer in the group.
-groups.
I will proceed to show that any group that contains the norm is also
a normalizer in the group.
DEPARTMENT OF MATHEMATICAL SCIENCES
BINGHAMTON UNIVERSITY
BINGHAMTON, NY. 13902-6000
smith at math.binghamton.edu
+++++++++++++++++++++++++++++++++++++++
The Layer Lemma
David Arden Jackson
We present a useful construction and lemma for creating finitely
generated monoids having specified numbers of ends for their
right and left Cayley digraphs.
SAINT LOUIS UNIVERSITY
220 NORTH GRAND, RITTER HALL ROOM 233
ST. LOUIS, MO 63103
jacksoda at slu.edu
+++++++++++++++++++++++++++++++++++++++
The Weyl Group and Coxeter Elements of 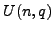
Julianne Rainbolt
This talk will review and describe the Weyl group of a finite
group of Lie type. The standard example when 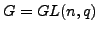 will be discussed as well as the example when
will be discussed as well as the example when 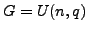 .
Included will be an examination of some relationships between the
Weyl groups of
.
Included will be an examination of some relationships between the
Weyl groups of 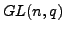 and
and 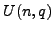 including their Coxeter elements.
including their Coxeter elements.
SAINT LOUIS UNIVERSITY
220 NORTH GRAND, RITTER HALL ROOM 233
ST. LOUIS, MO 63103
rainbolt at slu.edu
+++++++++++++++++++++++++++++++++++++++
On the Sources of Simple Modules in Nilpotent Blocks
Adam Salminen
I will state Puig's conjecture on the finite number of source
algebras for blocks of defect 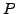 . Then I will show that for
a certain class of Nilpotent blocks we can reduce Puig's conjecture
to central
. Then I will show that for
a certain class of Nilpotent blocks we can reduce Puig's conjecture
to central 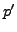 -extensions of simple groups.
-extensions of simple groups.
OHIO STATE UNIVERSITY
231 W. 18TH AVENUE
COLUMBUS, OH. 43210
salminen at math.ohio-state.edu
+++++++++++++++++++++++++++++++++++++++
A Generalization of Supersolvability
Tuval Shmuel Foguel
In this talk we consider a generalization of supersolvability
called groups of polycyclic breadth 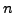 for
for 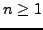 ,
we see that a number of well known results for supersolvable
groups generalize to groups of polycyclic breadth
,
we see that a number of well known results for supersolvable
groups generalize to groups of polycyclic breadth 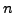 .
This generalization of supersolvability is especially strong for the
groups of polycyclic breadth
.
This generalization of supersolvability is especially strong for the
groups of polycyclic breadth 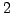 .
.
DEPARTMENT OF MATHEMATICS
AUBURN UNIVERSITY MONTGOMERY
3348 WALTON DR.
MONTGOMERY AL 36111
tfoguel at mail.aum.edu
+++++++++++++++++++++++++++++++++++++++
Homogeneous Products of Conjugacy Classes
Edith Adan-Bante
Let  be a finite group and
be a finite group and
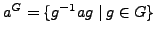 be the conjugacy class of
be the conjugacy class of 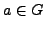 in
in  . Set
. Set
![$ [a,G]=\{a^{-1} a^g\mid g\in G\}$](img124.png) .
We can check that
.
We can check that
![$ a^G=a[a,G]$](img125.png) and thus
and thus
![$ \vert a^G\vert=\vert[a,G]\vert$](img126.png) .
.
Let 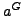 and
and 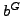 be conjugacy classes of
be conjugacy classes of  and
and
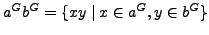 be the product of
be the product of 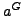 and
and 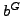 . We can check
that
. We can check
that 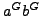 is a
is a  -invariant subset of
-invariant subset of  ,
that is
,
that is
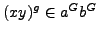 for any
for any
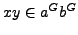 and any
and any 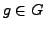 . Also, we can check that because
. Also, we can check that because
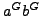 is a
is a  -invariant subset of
-invariant subset of  , then
, then 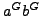 is the union of
is the union of 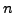 distinct conjugacy classes
distinct conjugacy classes
 , for some integer
, for some integer 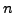 , and the conjugacy class
, and the conjugacy class 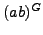 is a subset of
is a subset of
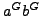 . Set
. Set
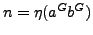 .
.
Under what circumstances is 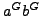 also a conjugacy
class, i.e.
also a conjugacy
class, i.e.
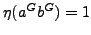 ? In this talk, we will prove the following
? In this talk, we will prove the following
Theorem 3
Let  be a finite group,
be a finite group,
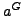 and
and 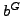 be conjugacy classes of
be conjugacy classes of 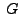 . Assume that
. Assume that
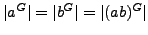 . Then
. Then
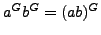 if and only if
if and only if
![$ [a,G]=[b,G]=[ab,G]$](img140.png) is a subgroup of
is a subgroup of 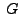 .
.
We will use the previous result to prove the following
Theorem 1
Let  be a finite nonabelian simple group and
be a finite nonabelian simple group and  be a conjugacy class of
be a conjugacy class of 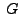 .
Then
.
Then
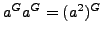 if and only if
if and only if 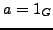 .
.
We turn then our attention when
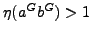 . We wonder what kind
of relationships exist among
. We wonder what kind
of relationships exist among
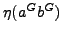 ,
, 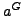 ,
, 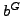 and
the structure of the group
and
the structure of the group  .
.
We consider the situation where, in addition, the group  is a
is a
 -group for some prime
-group for some prime  , that is the size of the set
, that is the size of the set  is a power of
is a power of  .
We can check then that given any conjugacy class
.
We can check then that given any conjugacy class 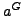 , the size of
, the size of
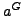 is a power of
is a power of  , that is
, that is 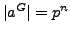 for some integer
for some integer 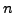 .
.
We will mention then other results in products of
conjugacy classes and finite  -groups.
The talk will be based on my papers
``On nilpotent groups and conjugacy classes",
``Homogeneous products of conjugacy classes" and
``Products of conjugacy classes and finite
-groups.
The talk will be based on my papers
``On nilpotent groups and conjugacy classes",
``Homogeneous products of conjugacy classes" and
``Products of conjugacy classes and finite  -groups". Those
papers are available on www.arxiv.org.
-groups". Those
papers are available on www.arxiv.org.
UNIVERSITY OF SOUTHERN MISSISSIPPI GULF COAST
730 EAST BEACH BOULEVARD
LONG BEACH MS 39560
Edith.Bante at usm.edu
+++++++++++++++++++++++++++++++++++++++
Characterizing injectors in finite solvable groups
Arnold David Feldman
(Joint work with Rex Dark, National University of Ireland, Galway).
We present characterizations of the injectors of a finite solvable
group that are independent of the original definition of injector
using Fitting sets. This can be considered a solution to a
problem posed by Doerk and Hawkes in their book
Finite Soluble Groups.
FRANKLIN & MARSHALL COLLEGE
LANCASTER, PA 17604-3003
afeldman at fandm.edu
+++++++++++++++++++++++++++++++++++++++
A Classification of Certain Maximal Subgroups of Symmetric Groups
Bret Jordan Benesh
Problem 12.82 of the Kourovka Notebook asks for all ordered pairs
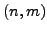 such that the symmetric group Sym
such that the symmetric group Sym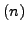 embeds in Sym
embeds in Sym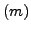 as a maximal subgroup. One family of such pairs is obtained when
as a maximal subgroup. One family of such pairs is obtained when
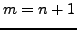 . Kaluznin and Klin and Halberstadt provided an
additional infinite family. This talk will present a third
infinite family of ordered pairs and show that no other pairs exist.
. Kaluznin and Klin and Halberstadt provided an
additional infinite family. This talk will present a third
infinite family of ordered pairs and show that no other pairs exist.
HARVARD UNIVERSITY
ONE OXFORD STREET
CAMBRIDGE, MA 02128
benesh at math.harvard.edu
+++++++++++++++++++++++++++++++++++++++
Finding Eigenvectors in the Minimal Polynomial
Charles Holmes
The following result is well known, but little known at least in most linear algebra texts and even by numerical analysts.
Result: Let 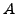 be a square matrix with minimal polynomial
be a square matrix with minimal polynomial 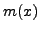 and
eigenvalue
and
eigenvalue 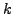 such that
such that
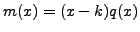 .
Then the non-zero columns of
.
Then the non-zero columns of 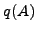 are eigenvectors of
are eigenvectors of 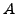 .
.
The proof is trivial. The main significance is that this observation
often yields the eigenvectors more easily than finding the reduced
row echelon form of 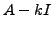 . In particular,
. In particular, 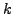 may not be known exactly.
Let
may not be known exactly.
Let
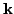 be the approximation for
be the approximation for 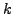 . Then
. Then
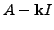 invertible,
so the eigenvectors can not be found in the usual way.
In this situation reasonably good approximations for the eigenvectors
may be found.
invertible,
so the eigenvectors can not be found in the usual way.
In this situation reasonably good approximations for the eigenvectors
may be found.
MIAMI UNIVERSITY
OXFORD, OH 45056
holmescs at muohio.edu
+++++++++++++++++++++++++++++++++++++++
An Embedding Theorem for Groups Universally Equivalent to Free Nilpotent Groups
Anthony Michael Gaglione
Let 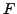 be a finitely generated (f.g.) nonabelian free group.
O. Kharlampovich and A. Myasnikov proved that any f.g. group
be a finitely generated (f.g.) nonabelian free group.
O. Kharlampovich and A. Myasnikov proved that any f.g. group 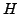 containing a distinguished copy of
containing a distinguished copy of 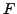 (
(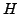 is called an
is called an 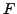 -group
in the algebraic geometry over groups) is universally equivalent to
-group
in the algebraic geometry over groups) is universally equivalent to 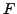 ( i.e., satisfies precisely the same universal sentences as
( i.e., satisfies precisely the same universal sentences as 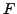 does in a first order language appropriate for group theory where
all the elements of
does in a first order language appropriate for group theory where
all the elements of 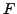 are taken as constants - called the language of
are taken as constants - called the language of 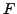 )
if and only if there is an embedding of
)
if and only if there is an embedding of 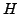 into a Lyndon's free
exponential group,
into a Lyndon's free
exponential group,
![$ F^{(Z[t])}$](img160.png) , which is the identity on
, which is the identity on 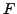 (this is called an
(this is called an 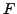 -embedding in the algebraic geometry over groups).
Alexei Myasnikov then posed the question as to whether or not a similar
result holds for f.g. free nilpotent groups with Lyndon's group replaced
with Philip Hall's completion with respect to a suitable binomial ring.
We (Dennis Spellman and I) answered Alexei's question in the affirmative.
This talk will explain our answer.
-embedding in the algebraic geometry over groups).
Alexei Myasnikov then posed the question as to whether or not a similar
result holds for f.g. free nilpotent groups with Lyndon's group replaced
with Philip Hall's completion with respect to a suitable binomial ring.
We (Dennis Spellman and I) answered Alexei's question in the affirmative.
This talk will explain our answer.
DEPARTMENT OF MATHEMATICS
U.S. NAVAL ACADEMY
572C HOLLOWAY ROAD
ANNAPOLIS, MD 21402-5002
amg at usna.edu
![]() -transitivity:
Every
-transitivity:
Every ![]() -subgroup of
-subgroup of ![]() is a
is a ![]() -subgroup of
-subgroup of ![]() .
.
![]() -persistence:
Every
-persistence:
Every ![]() -subgroup of
-subgroup of ![]() in
in ![]() is an
is an ![]() -subgroup of
-subgroup of ![]() .
.
![]() -transitive and
-transitive and
![]() -persistent subgroups.
-persistent subgroups.
![]() is extremely primitive if a point
stabiliser
is extremely primitive if a point
stabiliser ![]() is primitive on each of its orbits. Cyclic groups of prime
order, and doubly primitive groups provide infinite families of
examples. Efforts to classify the remaining examples (non-regular,
simply primitive) are the subject of the lecture.
A result of W. A. Manning from 1927
tells us that the stabiliser H acts faithfully on each of its
non-trivial orbits. Thus we have an embedding of a primitive group
is primitive on each of its orbits. Cyclic groups of prime
order, and doubly primitive groups provide infinite families of
examples. Efforts to classify the remaining examples (non-regular,
simply primitive) are the subject of the lecture.
A result of W. A. Manning from 1927
tells us that the stabiliser H acts faithfully on each of its
non-trivial orbits. Thus we have an embedding of a primitive group ![]() (or, rather, several primitive actions of
(or, rather, several primitive actions of ![]() ) in a larger primitive group
) in a larger primitive group
![]() . Specific examples of this embedding problem led to the construction
of several of the sporadic simple groups, and indeed sporadic groups
provide interesting examples of extremely primitive groups. The
classification divides into two cases - almost simple and affine - each
of which contributes interesting lists of examples. Our aim is to prove
that our lists are complete up to a finite number of exceptions. We have
achieved this in the affine case; the specificity of our results depends
on the strength of asymptotic bounds on the number of maximal subgroups
of almost simple groups.
. Specific examples of this embedding problem led to the construction
of several of the sporadic simple groups, and indeed sporadic groups
provide interesting examples of extremely primitive groups. The
classification divides into two cases - almost simple and affine - each
of which contributes interesting lists of examples. Our aim is to prove
that our lists are complete up to a finite number of exceptions. We have
achieved this in the affine case; the specificity of our results depends
on the strength of asymptotic bounds on the number of maximal subgroups
of almost simple groups.
![]() -local structure of a finite group gives a fusion system. But
there are examples
of fusion systems that do not occur in this way. We call these examples
exotic fusion systems.
Let
-local structure of a finite group gives a fusion system. But
there are examples
of fusion systems that do not occur in this way. We call these examples
exotic fusion systems.
Let ![]() be an algebraically closed field of characteristic
be an algebraically closed field of characteristic ![]() and
and ![]() a
finite group.
An interesting question for fusion systems is whether they can be obtained
from the local
structure of a block of the group algebra
a
finite group.
An interesting question for fusion systems is whether they can be obtained
from the local
structure of a block of the group algebra ![]() . In this talk I present a
joint work with Radha Kessar on some methods to reduce this question to
the case when
. In this talk I present a
joint work with Radha Kessar on some methods to reduce this question to
the case when ![]() is a
central
is a
central ![]() -extension of a simple group. As an application of our result,
we obtain that
the exotic fusion systems discovered by A. Ruiz and A. Viruel do not occur
as fusion systems of
-extension of a simple group. As an application of our result,
we obtain that
the exotic fusion systems discovered by A. Ruiz and A. Viruel do not occur
as fusion systems of ![]() -blocks of finite groups.
-blocks of finite groups.
![]() the function
the function
![]() denotes the smallest
integer
denotes the smallest
integer ![]() such that every element of the commutator subgroup
such that every element of the commutator subgroup ![]() is a product of
is a product of ![]() commutators. The statement that the set of
commutators of a group
commutators. The statement that the set of
commutators of a group ![]() does not form a subgroup is equivalent
to
does not form a subgroup is equivalent
to
![]() . For every prime
. For every prime ![]() , Guralnick has constructed
a
, Guralnick has constructed
a ![]() -group
-group ![]() of order
of order ![]() with
with
![]() .
For Cassidy's group
.
For Cassidy's group ![]() we have
we have
![]() .
However for given
.
However for given ![]() and any prime
and any prime ![]() , the group
, the group ![]() has a suitable homomorphic image
has a suitable homomorphic image
![]() such
that
such
that
![]() and
and ![]() has order
has order
![]() , where
, where ![]() is a linear function in
is a linear function in ![]() .
.
![]() was defined only as
was defined only as
![]() ,
where
,
where ![]() is the order of the smallest simple group in which the
elements of order
is the order of the smallest simple group in which the
elements of order ![]() do not form a subgroup.
do not form a subgroup.
![]() satisfies the
one-prime hypothesis if the greatest common
divisor of every pair of distinct ordinary
irreducible character degrees is either
satisfies the
one-prime hypothesis if the greatest common
divisor of every pair of distinct ordinary
irreducible character degrees is either ![]() or a
prime. In earlier work, Lewis was able to prove a
bound on the number of character degrees for a
solvable group
or a
prime. In earlier work, Lewis was able to prove a
bound on the number of character degrees for a
solvable group ![]() satisfying the one-prime
hypothesis and to show that the bound is best
possible.
satisfying the one-prime
hypothesis and to show that the bound is best
possible.
![]() satisfying
satisfying
![]() for a
nonabelian simple group
for a
nonabelian simple group ![]() , satisfying the
one-prime hypothesis. In particular, we show that
, satisfying the
one-prime hypothesis. In particular, we show that
![]() must be one of
must be one of ![]() , the Suzuki group
, the Suzuki group
![]() , or
, or
![]() with
with ![]() a power of a prime.
a power of a prime.
![]() be a finite group, and let
be a finite group, and let
![]() be the set of
irreducible character degrees
of
be the set of
irreducible character degrees
of ![]() .
We say that
.
We say that ![]() satisfies the One-prime hypothesis
if whenever
satisfies the One-prime hypothesis
if whenever
![]() and
and ![]() , then the greatest common
divisor of
, then the greatest common
divisor of ![]() and
and ![]() is either
is either ![]() or a prime.
In an earlier series of papers, I showed that if
or a prime.
In an earlier series of papers, I showed that if ![]() is
solvable and satisfies the one-prime
hypothesis, then
is
solvable and satisfies the one-prime
hypothesis, then
![]() , and
I gave examples of solvable groups satisfying the one-prime
hypothesis where the bound is met. In
this talk, I will show that if
, and
I gave examples of solvable groups satisfying the one-prime
hypothesis where the bound is met. In
this talk, I will show that if ![]() is a nonsolvable group
satisfying the one-prime hypothesis, then
is a nonsolvable group
satisfying the one-prime hypothesis, then
![]() .
In particular, I will show how classifying the almost simple
groups that satisfy the one-prime
hypothesis can be used to classify the nonsolvable groups
that satisfy the one-prime hypothesis.
.
In particular, I will show how classifying the almost simple
groups that satisfy the one-prime
hypothesis can be used to classify the nonsolvable groups
that satisfy the one-prime hypothesis.
![]() and
and ![]() be conjugacy classes of
be conjugacy classes of ![]() and
and
![]() be the product of
be the product of ![]() and
and ![]() . We can check
that
. We can check
that ![]() is a
is a ![]() -invariant subset of
-invariant subset of ![]() ,
that is
,
that is
![]() for any
for any
![]() and any
and any ![]() . Also, we can check that because
. Also, we can check that because
![]() is a
is a ![]() -invariant subset of
-invariant subset of ![]() , then
, then ![]() is the union of
is the union of ![]() distinct conjugacy classes
distinct conjugacy classes
![]() , for some integer
, for some integer ![]() , and the conjugacy class
, and the conjugacy class ![]() is a subset of
is a subset of
![]() . Set
. Set
![]() .
.
![]() also a conjugacy
class, i.e.
also a conjugacy
class, i.e.
![]() ? In this talk, we will prove the following
? In this talk, we will prove the following
![]() . We wonder what kind
of relationships exist among
. We wonder what kind
of relationships exist among
![]() ,
, ![]() ,
, ![]() and
the structure of the group
and
the structure of the group ![]() .
.
![]() is a
is a
![]() -group for some prime
-group for some prime ![]() , that is the size of the set
, that is the size of the set ![]() is a power of
is a power of ![]() .
We can check then that given any conjugacy class
.
We can check then that given any conjugacy class ![]() , the size of
, the size of
![]() is a power of
is a power of ![]() , that is
, that is ![]() for some integer
for some integer ![]() .
.
![]() be a finite
be a finite ![]() -group, for some prime
-group, for some prime ![]() ,
and
,
and ![]() be a conjugacy classes of
be a conjugacy classes of ![]() with
with ![]() , for some
integer
, for some
integer ![]() . Then
. Then
![]() -groups.
The talk will be based on my papers
``On nilpotent groups and conjugacy classes",
``Homogeneous products of conjugacy classes" and
``Products of conjugacy classes and finite
-groups.
The talk will be based on my papers
``On nilpotent groups and conjugacy classes",
``Homogeneous products of conjugacy classes" and
``Products of conjugacy classes and finite ![]() -groups". Those
papers are available on www.arxiv.org.
-groups". Those
papers are available on www.arxiv.org.
![]() . In particular,
. In particular, ![]() may not be known exactly.
Let
may not be known exactly.
Let
![]() be the approximation for
be the approximation for ![]() . Then
. Then
![]() invertible,
so the eigenvectors can not be found in the usual way.
In this situation reasonably good approximations for the eigenvectors
may be found.
invertible,
so the eigenvectors can not be found in the usual way.
In this situation reasonably good approximations for the eigenvectors
may be found.