Group Theory Abstracts

Conjugacy classes for 2-generator p-groups of nilpotency class 2

AZHANA AHMAD, Universiti Sains Malaysia

The classification for $2$ -generator $p$ -groups of class $2$ has been completed by Morse, Magidin and Ahmad. Using this classification, we give formulas for the number and size of conjugacy classes of these groups.

UNIVERSITI SAINS MALAYSIA
PENANG, MALAYSIA
azhana79 at yahoo dot com

Solitary Solvable II

RISTO ATANASOV, Western Carolina University

A subgroup $H$ of a group $G$ is a solitary subgroup of $G$ if $G$ does not contain another isomorphic copy of $H$ . A normal subgroup $N$ of a group $G$ is a normal solitary subgroup of $G$ if $G$ does not contain another normal isomorphic copy of $N$ . A group $G$ is (normal) solitary solvable if it has a sub-(normal) solitary series $\{1\}=H_0\le H_1\le \dots \le H_n=G$ with $\frac{H_{i+1}}{H_i}$ abelian.

WESTERN CAROLINA UNIVERSITY
CULLOWHEE, NC
ratanasov at email dot wcu dot edu

Normally serially monomial $p$ -groups

TIM WALSH BONNER, Texas State University - San Marcos

We define a $p$ -group, $P$ , to be normally serially monomial if there exists a single normal series,

$$P = P_0 \geq P_1 \geq \ldots \geq P_{n-1} \geq P_{n} = 1_P,$$

such that $\left\vert P_{i - 1}/P_{i}\right\vert = p$ for $i \in \left\{1, \ldots, n\right\}$ , and for every $\chi \in$   Irr$\left(P\right)$ , there exists $P_j$ with $0 \leq j \leq n$ and $\lambda \in$   Irr$\left(P_j\right)$ , such that $\lambda$ is linear and $\lambda^{P} = \chi$ . We investigate the character theoretic properties of such groups and the relation of the character degrees (and their multiplicities) to the group theoretic structure. Specifically, we show for $i \in \left\{1, \ldots, n\right\}$ ,

$$\left\vert \left\{\chi \in \text{Irr}(P)~\vert~\chi(1_P) = p^{i} ... ...me}_{i}\right] - \left[P_{i}:P^{\prime}_{i - 1}\right]}{\left[P:P_{i}\right]}.$$

TEXAS STATE UNIVERSITY - SAN MARCOS
SAN MARCOS, TX
timwbonner at gmail dot com

Subgroups of a Direct Product which Satisfy the Frattini Argument

BEN BREWSTER, Binghamton University

A subgroup $H$ of a group $G$ satisfies the Frattini argument in $G$ provided for each subgroup $K$ normal in $G$ , $G = K N(H \cap K)$ . Examples of subgroups which satisfy the Frattini argument are injectors for a Fitting set. In a current project with J. Evan and S. Reifferscheid, we have obtained that if $G= A \times B$ , and $H$ satisfies the Frattini argument in $G$ , then the diagonal sections (projection mod intersection with coordinate) are nilpotent but need not be abelian.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
ben at math dot binghamton dot edu

On the derived length of a Coxeter group

PETER ALAN BROOKSBANK, Bucknell University

In this talk I will present some observations about the derived length of a Coxeter group. In particular, I will give necessary and sufficient conditions for a Coxeter group to be "almost perfect". This is a report on current joint work with A. Piggott.

BUCKNELL UNIVERSITY
LEWISBURG, PA
pbrooksb at bucknell dot edu

An explicit bijection for the Alperin weight conjecture

for the symmetric groups

JAMES COSSEY, University of Akron

The Alperin weight conjecture - which proposes that the number of Alperin weights of a finite group $G$ is equal to the number of $p$ -regular conjugacy classes of $G$ , where $p$ is a prime, is known to be true for $S_n$ . However, in the original proof of Alperin and Fong, no explicit bijection is given between the two sets. Since the $p$ -regular conjugacy classes of $S_n$ are indexed by the $p$ -regular partitions of $n$ , then it would be nice to find an explicit bijection from the $p$ -regular partitions of $n$ to the Alperin weights of $S_n$ . While we are not yet able to do this, we can construct an explicit bijection from a related set of partitions to the Alperin weights of $S_n$ .

UNIVERSITY OF AKRON
AKRON, OH
cossey at uakron dot edu

Ternary division rings and their groups

CLIFTON EDGAR EALY JR,, Department of Mathematics,

Western Michigan University

In his 1943 TAMS paper, "Projective Planes", Marshall Hall Jr., introduced the idea of a ternary ring. In this talk, $(R,T)$ is a ternary ring if $R$ has distinct elements 1 and 0 with $T$ mapping $R\times R\times R$ into $R$ such that:

T1. $T(0,m,c)=T(m,0,c)=c$

and

T2. $T(1,m,0)=T(m,1,0)=m$ for all $m,c$ in $R$ .

Following M. Hall Jr., using $T$ , we may introduce binary operations $+$ ,$*$ on $R$ so that $(R, +)$ and $(R\setminus \{0\},*)$ are groupoids with identity 0,1 respectively. We call $(R,T)$ a ternary division ring if $(R, +)$ and $(R\setminus \{0\},*)$ are quasigroups with identity 0,1 respectively. We briefly discuss the double pointed categories TrnR and TrnDR of ternary rings and ternary division rings respectively. Finally, we focus our attention on a fixed ternary division ring $(D,T)$ and its groups.

DEPARTMENT OF MATHEMATICS, WESTERN MICHIGAN UNIVERSITY
KALAMAZO, MI
clifton dot e.ealy at wmich dot edu

MOLS based on nonabelian groups

ANTHONY BRIAN EVANS, Wright State University

Given a finite group $G$ , how many squares are possible in a set of mutually orthogonal latin squares based on $G$ ? This question has been answered for elementary abelian groups, groups of small order, and groups with nontrivial, cyclic Sylow $2$ -subgroups. We will describe lower bounds for the number of squares possible in sets of mutually orthogonal latin squares based on nonabelian groups.

WRIGHT STATE UNIVERSITY
DAYTON, OH
anthony dot evans at wright dot edu

A generalization of t-groups

ARNOLD D. FELDMAN, Franklin & Marshall College

A $t$ -group is a group all of whose subnormal subgroups are normal. It is possible to define a $t_{\cal F}$ -group, one in which all ${\cal F}$ -subnormal subgroups are normal, where ${\cal F}$ is a formation of solvable groups locally defined by a formation function with appropriate properties. If ${\cal N}$ is the formation of nilpotent groups, the $t_{\cal N}$ -groups are just the $t$ -groups, whereas if ${\cal S}$ is the formation of solvable groups, the $t_{\cal S}$ -groups are just the Dedekind groups. This talk will describe possibilities for the property of being a $t_{\cal F}$ -group when ${\cal F}$ is between these extremes, investigating how to tell whether distinct formations yield distinct such properties.

FRANKLIN & MARSHALL COLLEGE
LANCASTER, PA
afeldman at fandm dot edu

Solitary solvable subgroups

TUVAL FOGUEL, Western Carolina University

A subgroup $H$ of a group $G$ is a solitary subgroup of $G$ if $G$ does not contain another isomorphic copy of $H$ . A normal subgroup $N$ of a group $G$ a normal solitary subgroup of $G$ if $G$ does not contain another normal isomorphic copy of $N$ . A group $G$ is (normal) solitary solvable if is has a sub-(normal) solitary series $\{1\}=H_0\le H_1\le \dots \le H_n=G$ with $\frac{H_{i+1}}{H_i}$ abelian.

In this talk we will look at finite (normal) solitary solvable groups.

WESTERN CAROLINA UNIVERSITY
CULLOWHEE, NC
tsfoguel at wcu dot edu

Conjugation and Inverse Semigroups

FERNANDO GUZMAN, Binghamton University

We'll consider the connection between conjugation in groups and semigroups with inverse semigroups. This is work in progress.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
fer at math dot binghamton dot edu

Nonabelian tensor products: the mystery of compatible actions

LUISE-CHARLOTTE KAPPE, Binghamton University

Let $G$ and $H$ be groups acting on each other and acting on themselves by conjugation, where $^gg' = gg'g^{-1}$ and $^hh' hh'h^{-1}$ for $g,g' \in G$ and $h,h' \in H$ . We say the mutual actions are compatible if

$$^{(^gh)}g' =\ ^g(^h(^{g^{-1}}g'))\ \ \ ^{(^hg)}h' =\ ^h(^g(^{h^{-1}}h'))$$

for all $g,g' \in G$ and $h,h' \in H$ .

Compatible actions play a role in the nonabelian tensor product defined as follows.

$\parbox{4.5in}{\it Let $G$\ and $H$\ be groups which act on each oth... ...the group generated by $g\otimes h$ for $g\in G$\ and $h\in H$\ with relations}$

$$\begin{aligned}gg' \otimes h &= (^gg'\otimes\ ^gh)(g\otimes h)\\ g\otimes hh' &= (g\otimes h)(^hg\otimes\ ^hh'). \end{aligned}$$

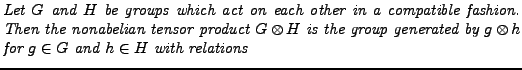
Little is known about compatible actions. This is due in part to the fact that little is known about the automorphism groups in general. But even if we know the automorphism groups, like in the case of cyclic groups, our knowledge consists of fragments.

The topic of this talk is to shed some light on the mystery of compatible actions. We will give a brief overview on what is known so far, provide some new results in case of cyclic groups, and discuss various approaches on how to unravel this mystery further.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
menger at math dot binghamton dot edu

Groups in which all subgroups are permutable or of finite rank

ZEKERIYA YALCIN KARATAS, University of Alabama

In this talk, we will go over some results about groups in which all subgroups are permutable or of finite rank. We will show the solubility of these type of groups in certain classes. Also we will obtain a bound for the cases when these groups are soluble.

UNIVERSITY OF ALABAMA
TUSCALOOSA, AL
yzkaratas at crimson dot ua dot edu

Groups with few conjugacy classes

THOMAS MICHAEL KELLER, Texas State University

We present a lower bound for the number of conjugacy classes of a finite group in terms of the largest prime divisor of the group order. We also present examples for which this bound is best possible. It is conjectured that these examples are the only ones meeting this bound, and we discuss recent progress on this conjecture (joint work with Hethelyi, Horvath, Maroti).

TEXAS STATE UNIVERSITY
SAN MARCOS, TX
tk04 at txstate dot edu

Closure operators on the subgroup lattice of the group G

MARTHA KILPACK, Binghamton University

Let G be an infinite group and let Sub(G) := $\{ H\ :\ H\ subgroup\ of\ G \}$ . (Sub(G), $\subseteq$ ) forms a lattice. We can then look at the set of all closure operators on Sub(G) ($\Phi$ (Sub(G)), which also forms a lattice. In this talk we will take a look at possible properties, including an algebraic property, of the lattice $\Phi$ (Sub(G).

BINGHAMTON UNIVERSITY
ENDWELL, NY
kilpack at math dot binghamton dot edu

On Automorphism groups of Cayley-Dickson loops

JENYA KIRSHTEIN, University of Denver

Cayley-Dickson loop (L,*) is a loop of basis units of an algebra constructed by Cayley-Dickson doubling process (the first few examples of such algebras are complex numbers, quaternions, octonions, sedenions). We will discuss properties of Cayley-Dickson loops, identities they satisfy and the structure of their automorphism groups.

UNIVERSITY OF DENVER
DENVER, CO
ykirshte at du dot edu

The Subgroup Lattice for $Q_8 \times Q_8$

DANDRIELLE LEWIS, Binghamton University

In group theory, examining a group and studying its subgroups and their respective properties is interesting. In this talk, I will state a very exciting result which characterizes a containment of subgroups in a direct product. I will also give an application of this result; specifically the construction of the lattice of $Q_{8} \times Q_{8}$ .

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
dlewis5 at binghamton dot edu

Lifts and generalized vertices for Brauer characters

of solvable groups

MARK L. LEWIS, Kent State University

Let $G$ be a solvable group and let $\phi$ be a $p$ -Brauer character of $G$ where $p$ is an odd prime. We say $\chi$ is a lift of $\phi$ if $\phi$ is the restriction of $\chi$ to the $p$ -regular elements of $G$ .

We show that the generalized vertices for $\chi$ are all conjugate and if $(Q,\delta)$ is a generalized vertex for $\chi$ , then $Q$ is a vertex for $\phi$ and $\delta$ is linear. With this result in hand, we show that if $\phi$ has an abelian vertex $Q$ , then $\phi$ has at most $\vert Q:Q'\vert$ lifts. Finally, we discuss what is needed to prove this for any vertex $Q$ . (This is joint work with James P. Cossey.)

KENT STATE UNIVERSITY
KENT, OH
lewis at math dot kent dot edu

Quadratic offenders and Oliver's $p$ -group conjecture

JUSTIN LYND, The Ohio State University

Bob Oliver conjectures that if $p$ is an odd prime and $S$ is a finite $p$ -group, then the Thompson subgroup $J(S)$ is contained in a certain characteristic subgroup $\mathfrak{X}(S)$ , which is now known as the Oliver subgroup. This conjecture would imply the existence and uniqueness of centric linking systems for fusion systems over odd primes.

Oliver's conjecture has a module-theoretic reformulation due to Green, Hethelyi, and Lillienthal. The main question arising out of this reformulation is the following: for $p$ an odd prime, $G$ a finite $p$ -group and $V$ an ${\bf F}_p[G]-module$ , does the presence of certain ``large" quadratic subgroups in $G$ force the existence of quadratic elements in the center of $G$ ? I will present recent work on this question which settles Oliver's conjecture in a couple of special cases, including for $G = S/\mathfrak{X}(S)$ of nilpotence class at most roughly the (base 2) logarithm of $p$ .

THE OHIO STATE UNIVERSITY
COLUMBUS, OH
jlynd at math dot ohio-state dot edu

Nonabelian tensor squares and cartesians of

nilpotent products: a preliminary report.

ARTURO MAGIDIN, University of Louisiana at Lafayette

If $G$ and $K$ are groups, the $c$ -nilpotent product of $G$ and $K$ is defined to be $(G*K)/([G,K]\cap (G*K)_{c+1})$ , where $G*K$ is the free product of $G$ and $K$ , and $(G*K)_{c+1}$ is the $(c+1)$ st term of the lower central series of $G*K$ . Golovin proved in the 1950s that every element of the $c$ -nilpotent product can be written uniquely as $gku$ , where $g\in G$ , $k\in K$ , and $u\in[G,K]$ , the latter called the cartesian of the nilpotent product. In 1960, MacHenry proved that the cartesian of the $2$ -nilpotent product is isomoprhic to $G^{\rm ab}\otimes K^{\rm ab}$ via the map $[g,k]\mapsto \overline{g}\otimes\overline{k}$ .

Using a construction introduced by Rocco to compute the nonabelian tensor square of a group, we show that if $G_c\neq 1$ , then the cartesian of the $c$ -nilpotent product of $G$ with itself has the nonabelian tensor square of $G$ as a quotient. We explore this connection, with the hope of getting insight into both the tensor square and the cartesian of a $c$ -nilpotent product.

UNIVERSITY OF LOUISIANA AT LAFAYETTE
LAFAYETTE, LA
magidin at member dot ams dot org

Groups whose the nonabelian tensor squares are abelian

ROHAIDAH MASRI, Sultan Idris Education University (UPSI)

If the nonabelian tensor square of a group $G$ is abelian then the derived subgroup of $G$ is abelian. This follows from the fact that an epimorphism from $G\otimes G$ to $G'$ always exists. Hence those groups whose nonabelian tensor squares abelian are metabelian. However, the converse is not true. Let $G$ is free nilpotent of class 3. Then $G$ is metabelian but $G\otimes G$ is nilpotent of exactly class 2 (Blyth, Moravec, Morse, 2008). The purpose of this paper is to precisely define the subclass of metabelian groups whose nonabelian tensor squares are abelian.

SULTAN IDRIS EDUCATION UNIVERSITY (UPSI)
TANJONG MALIM, PERAK, MALAYSIA
rohaidah at fst dot upsi dot edu dot my

Unramified Brauer groups of finite and infinite groups

PRIMOZ MORAVEC, University of Ljubljana

The Bogomolov multiplier is a group theoretical invariant isomorphic to the unramified Brauer group of a given quotient space, and represents an obstruction to the problem of stable rationality. We describe a homological version of the Bogomolov multiplier, find a five term exact sequence corresponding to this invariant, and describe the role of the Bogomolov multiplier in the theory of central extensions. We define the Bogomolov multiplier within K-theory and show that proving its triviality is equivalent to solving a problem posed by Bass. An algorithm for computing the Bogomolov multiplier is presented.

UNIVERSITY OF LJUBLJANA
LJUBLJANA, SLOVENIA
primoz dot moravec at fmf dot uni-lj dot si

On the capability of certain $p$ -groups of class 2

ROBERT FITZGERALD MORSE, University of Evansville

In this talk we consider the capability of $p$ -groups of nilpotency class 2 of exponent $p$ and $p$ -groups in which $G'=Z(G)$ and $G'$ is elementary abelian of rank 2.

UNIVERSITY OF EVANSVILLE
EVANSVILLE, IN
rfmorse at evansville dot edu

Nilpotent subgroups of class $\leq 2$ of maximal order

ANNI NEUMANN, University of Tübingen

This talk is a part of my work about conjugacy of $\mathcal{N}$ -maximal subgroups of a finite group $G$ containing a nilpotent subgroup of class $\leq 2$ of maximal order. We study the operation of groups $A \in \mathcal{A}_2(G)$ (the set of nilpotent subgroups of class $\leq 2$ of maximal order) on the set of components of $G$ . Then we get the important result:

Theorem. Let $G$ be a finite group, $A \in \mathcal{A}_2(G)$ , $E$ a component of $G$ with $E/Z(E)\not \simeq PSL(2,2^m), m\geq 2$ and $E/Z(E) \not \simeq PSL(2,9)$ .
Then $A \subseteq N_G(E)$ .

UNIVERSITY OF TÜBINGEN
TÜBINGEN, GERMANY
av dot neumann at mymail dot ch

Solvability conditions for complex $p$ -solvable linear groups

BEN NEWTON, Beloit College

We present conditions on the structure and degree $n$ of a finite irreducible complex linear group that guarantee its solvability. In particular, we show that if such a group is $p$ -solvable but not $p$ -closed for some prime number $p$ , then the group is solvable whenever $n \equiv \pm 1 \pmod{p}$ and $n$ is also smaller than certain bounds which are on the order of $p2$ .

BELOIT COLLEGE
BELOIT, WI
newtonb at beloit dot edu

On the covering numbers of groups

DANIELA B. NIKOLOVA-POPOVA, Florida Atlantic University

According to Bernhard Neumann, every group with a noncyclic finite homomorphic image is the union of finitely many proper subgroups. The minimal number of subgroups needed to cover a group $G$ is called the covering number of $G$ . Tomkinson showed that for a solvable group the covering number is of the form prime power plus one and he suggested the investigation of the covering number for families of finite simple groups. So far, a few results are known, among them some for small alternating groups, several types of linear groups, and the Suzuki groups. For sporadic simple groups the covering numbers are known for the Matthieu groups $M_{11}, M_{22}$ and $M_{23}$ , as well as Ly and O'N. Furthermore, estimates have been given for J1 and McL. We have started to determine the covering number for other sporadic simple groups such as the Matthieu group $M_{12}$ .

FLORIDA ATLANTIC UNIVERSITY
BOCA RATON, FL
nikolova20032003 at yahoo dot com

A characteristic subgroup for fusion systems

SILVIA ELENA ONOFREI, The Ohio State University

Let $\mathcal{F}$ be a saturated fusion system on a finite $p$ -group $S$ , where $p$ is a prime. Following an approach developed by Stellmacher for finite groups, I will define a certain positive characteristic functor $S \rightarrow W(S)$ . As a counterpart for the prime $2$ to Glauberman's $ZJ$ -theorem, Stellmacher proved that any nontrivial $2$ -group $S$ has a nontrivial characteristic subgroup $W(S)$ with the following property. For any finite $\Sigma_4$ -free group $G$ , with $S$ a Sylow $2$ -subgroup of $G$ and with $O_2(G)$ self-centralizing, the subgroup $W(S)$ is normal in $G$ . I will show how to generalize Stellmacher's result to fusion systems. For odd primes, the functor $S \rightarrow W(S)$ is used to generalize Thompson's normal complement theorem to fusion systems. This is work done in collaboration with Radu Stancu.

THE OHIO STATE UNIVERSITY
COLUMBUS, OH
onofrei at math dot ohio-state dot edu

The Free Nilpotent Groups of Finite Rank -

A Preliminary Report

MARK PEDIGO, Saint Louis University

In their article, ``On the derived subgroup of the free nilpotent groups of finite rank'', Russell Blyth, Primoz Moravec, and Robert Morse apply the work of S. Moran's ``A subgroup theorem for free nilpotent groups'' to discuss the structure of the derived subgroups of the free nilpotent groups of finite rank. Specifically, they construct an isomorphism for such a derived subgroup in terms of a direct product of a nonabelian group and a free abelian group. Having accomplished this feat, they then apply this result to computing the nonabelian tensor squares of the free nilpotent groups of finite rank.

In this talk, we discuss expansions of this research to investigate the structure of all of the other members of the lower central series and of the derived series of a free nilpotent group of finite rank.

SAINT LOUIS UNIVERSITY
SAINT LOUIS, MO
mark dot pedigo at gmail dot com

Counting subgroups in a direct product of finite cyclic groups

JOSEPH PETRILLO, Alfred University

In this talk, we will calculate the number of subgroups in a direct product of finite cyclic groups by applying the fundamental theorem of finite abelian groups and a well-known structure theorem due to Goursat. We will also suggest ways in which the results can be generalized to a direct product of arbitrary finite groups.

ALFRED UNIVERSITY
ALFRED, NY
petrillo at alfred dot edu

Moufang loops of order 81

ANDREW RAJAH, School of Mathematical Sciences,

Universiti Sains Malaysia

Analyzing the properties possessed by a nonassociative Moufang loop of order 81, we show that such a loop could be either of exponent three or nine. The general product rule of such a loop is governed by four parameters for the first case, and three for the second. Then by studying all possible values of these parameters, we find that there exist only five non-isomorphic cases: three of exponent three and two of exponent nine.

SCHOOL OF MATHEMATICAL SCIENCES, UNIVERSITI SAINS MALAYSIA
PENANG, MALAYSIA
andy at cs dot usm dot my

Faithful irreducible characters of subgroups of

wreath product $p$ -groups

JEFFREY M. RIEDL, University of Akron

Let $p$ be a prime and let $P$ be a Sylow $p$ -subgroup of the symmetric group of degree $p^3$ . The group $P$ contains an "easy to see" normal subgroup $B$ that is elementary abelian of rank $p^2$ . For the subgroups $H$ of $P$ having a unique minimal normal subgroup, our goal is to calculate the number of faithful irreducible ordinary characters of $H$ of each degree. Part of our motivation is that under certain circumstances the number of such characters of $H$ of degree $p^2$ is related to the order of the automorphism group $Aut(H)$ . We have achieved our goal for all subgroups $H$ satisfying all of the following conditions: (1) $H$ splits over its normal subgroup $H\cap B$ , (2) the factor group $H/(H\cap B)$ has exponent $p^2$ , and (3) the order of $H\cap B$ is $p^n$ where $n$ is divisible by $p$ .

UNIVERSITY OF AKRON
AKRON, OH
riedl at uakron dot edu

The Schur multiplier of a generalized Baumslag-Solitar group

DEREK SCOTT ROBINSON, University of Illinois

at Urbana-Champaign

A generalized Baumslag-Solitar group is the fundamental group of a graph of groups with infinite cyclic vertex and edge groups. A method is described for calculating the Schur mutiplier of an arbitrary group of this type.

UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
URBANA, IL
dsrobins at illinois dot edu

Finite solvable groups in which subnormal subgroups permute

with system normalizers

JACK SCHMIDT, University of Kentucky

The holomorph of a cyclic group of odd prime power order is a good example of a group in which subnormal subgroups permute with all Sylow system normalizers, but may not permute with the Sylow subgroups themselves. This example is also indicative of the full classification, at least amongst those groups whose nilpotent residual has nilpotency class at most two. This is joint work with Jim Beidleman and Hermann Heineken.

UNIVERSITY OF KENTUCKY
LEXINGTON, KY
jack at ms dot uky dot edu

Character degrees of maximal class 5-groups

MICHAEL CHARLES SLATTERY, Marquette University

This talk will present limits on the possible sets of irreducible character degrees of a normally monomial 5-group of maximal class.

MARQUETTE UNIVERSITY
MILWAUKEE, WI
mikes at mscs dot mu dot edu

A general construction for the box-tensor product

VIJI ZACHARIAH THOMAS , Binghamton University

We introduce a generalization of the non-abelian tensor product. Let $G$ and $H$ be groups which act on each other and which act on themselves. The actions of $G$ and $H$ are said to be compatible, if $^{(^ab)}c=\;^a(^b(^{a^{-1}}c))$ for all $a,b,c\in G\cup H$ . The box-tensor product $G\boxtimes H$ is defined provided $G$ and $H$ act on each other compatibly. In such a case $G\boxtimes H$ is the group generated by the symbols $g\boxtimes h$ with relations $gg'\boxtimes h=(^gg'\boxtimes \;^gh)(g\boxtimes h)\;$ and $g\boxtimes hh'=(g\boxtimes h)(^hg\boxtimes \;^hh')$ , for all $g,g' \in G$ and $h,h' \in H$ . Note that if the groups act on themselves by conjugation, then the box tensor product is the nonabelian tensor product. In this talk we give a general construction for the box-tensor product $G\boxtimes H$ . We describe the box-tensor product as a subgroup of a quotient of the free product $G\ast H$ . Such a construction was given by N R Rocco as well as Ellis and Leonard indepen dently for the nonabelian tensor product. We will discuss some examples of box-tensor product.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
vthomas at math dot binghamton dot edu

pt

The Brauer-Clifford group of $G$ -rings

ALEXANDRE TURULL, University of Florida

Let $G$ be a finite group. Traditionally, the representation theory of $G$ considers a commutative ring $R$ , and then studies modules $M$ over $R$ on which $G$ acts where the actions of $R$ and $G$ on $M$ obey some compatibility properties. When $R$ is instead a commutative $G$ -ring, one defines similarly $G$ -modules over $R$ , where the compatibility now takes into account the action of $G$ on $R$ . The traditional notion of module $M$ over a ring $R$ is then simply a $G$ -module over the $G$ -ring $R$ , where we take the action of $G$ on $R$ to be trivial. The author has defined the notion of the Brauer-Clifford group of certain $G$ -algebras over fields. The Brauer-Clifford group is useful for the study of Clifford theory of finite groups, and in particular, it has been used to prove a strengthened version of the McKay Conjecture for all finite $p$ -solvable groups. We see how, by incorporating the study of $G$ -modules over commutative $G$ -rings, we may give a natural definition of the Brauer-Clifford group of $G$ -rings. This simpler definition extends the definition of the Brauer-Clifford group, and provides a more flexible basis for applications to the Clifford theory of finite groups.

UNIVERSITY OF FLORIDA
GAINESVILLE, FL
turull at ufl dot edu

Group theory in loop theory

PETR VOJTECHOVSKY, University of Denver

This is a brief and incomplete overview of open and recently solved problems in loop theory (loops are ``nonassociative groups'') in which group theory plays a crucial role. I will speak about automorphic loops, loops with commuting inner mappings, and Moufang loops.

UNIVERSITY OF DENVER
DENVER, CO
petr at math dot du dot edu

Coverings of p-groups by groups of order $p^2$ and simple rings

GARY LEE WALLS, Southeastern Louisiana University

A covering $C$ of a group $G$ is a collection of subgroups of $G$ so that for all $x \in G$ , there exists an $H \in C$ so that $x \in H$ . Whenever $C$ consists of only abelian subgroups, there is a natural way to associate a ring with the cover $C$ , namely by defining $R_C(G)=\{ f: G \rightarrow G \ \vert \$    for each $H \in C, \ f \vert _H \in End(H) \}$ . Here the $f's$ are just functions and the operations are function addition and composition of functions. We are interested in how properties of this ring can influence structural properties of the group $G$ .

In this paper we consider the situation in which $G$ is a p-group and $C$ is a covering by groups which are elementary abelian of order $p2$ . We can associate a graph with each such cover. This graph can then be used to determine properties of the ring, in particular, it can be used to decide when the ring is simple.

As a consequence, we are able to show that unless a p-group of exponent $p$ has an element whose centralizer has order $p2$ , there will exist a covering of this group for which the ring is not simple.

This theorem leads to a general discussion of p-groups which have an element of order $p$ whose centralizer has order $p2$ . It turns out that all such groups must be of maximal class.

SOUTHEASTERN LOUISIANA UNIVERSITY
HAMMOND, LA
gary dot walls at selu dot edu

Cayley-Sudoku Tables and Transversals

MICHAEL B. WARD, Western Oregon University

Any Cayley table is a Latin square, two-thirds of being a Sudoku-like table. Cayley-Sudoku tables are Cayley tables arranged in such a way as to satisfy the additional Sudoku requirement, namely, that the Cayley table is divided into rectangular blocks with each group element appearing exactly once in each block. A recreational math project with undergraduates on constructing Cayley-Sudoku tables led to this potentially interesting question about transversals. Given a subgroup $H$ of a (finite) group $G$ , under what circumstances is it possible to partition $G$ into sets $L_{1}, L_{2}, \ldots, L_{k}$ where for every $g\in G$ each $L_i$ is a left transversal of $H^{g}$ ? After some remarks on Cayley-Sudoku tables for motivation, we present what we know about the transversal question from a group theoretic and then a combinatorial perspective, with the hope that some listener will know more.

WESTERN OREGON UNIVERSITY
MONMOUTH, OR
wardm at wou dot edu

If the Base of a Wreath Product is not Characteristic

ELIZABETH WILCOX, Binghamton University

We'll discuss the consequences of knowing that the base of a finite permutational wreath product is not characteristic. Much has been discovered in this topic in the case of standard wreath products and wreath products $G \wr H$ where $H$ acts transitively, but we'll discuss finite wreath products where the action of $H$ is only faithful. The talk will develop an understanding of centralizers in a wreath product from a new viewpoint and examine the number of conjugates with which a given element may commute. This will ultimately lead to the conclusion that if the base of a finite permutational wreath product $G \wr H$ is not characteristic then $G$ must equal $A \rtimes \langle x \rangle$ where $A$ is an odd order abelian group on which $x$ , an element of order 2, acts by inversion.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
wilcox at math dot binghamton dot edu

Isometry groups of bilinear maps

JAMES WILSON, The Ohio State University

We prove a structure theorem for the isometry group of an Hermitian map $b\colon V\times V\to W$ , where $V$ and $W$ are vector spaces over a finite field of odd order. We also present a Las Vegas polynomial-time algorithm to find generators for this isometry group, and to determine its structure. The algorithm can be adapted to construct the intersection of the members in a set of classical subgroups of ${\rm GL}(V)$ , yielding the first polynomial-time solution of this old problem. Our approach develops new computational tools for algebras with involution, which in turn have applications to other algorithmic problems of interest. An implementation of our algorithm in the Magma system demonstrates its practicability.

THE OHIO STATE UNIVERSITY
COLUMBUS, OH
wilson at math dot ohio-state dot edu

Regular orbits of nilpotent subgroups of solvable groups

YONG YANG, Texas State University at San Marcos

We settle a conjecture by Walter Carlip. Suppose $G$ is a finite solvable group, $V$ is a faithful $G$ -module over a field of characteristic $p$ and assume $O_p(G)=1$ . Let $H$ be a nilpotent subgroup of $G$ and assume that $H$ involves no wreath product $Z_r \wr Z_r$ for $r=2$ or $r$ a Mersenne prime, then $H$ has at least one regular orbit on $V$ .

TEXAS STATE UNIVERSITY AT SAN MARCOS
SAN MARCOS, TX
yang at txstate dot edu