Group Theory Abstracts

Integral sets in finite groups

ROGER ALPERIN, Dept. of Mathematics/ San Jose State University

I will discuss the boolean algebra of integral sets of a finite group.

DEPT. OF MATHEMATICS/ SAN JOSE STATE UNIVERSITY
SAN JOSE, CA
rcalperin at gmail dot com

Automorphism groups of homogeneous groups

DAVID PETER BIDDLE, Binghamton University

The quaternions $Q=Q_8$ have the property that $\mathrm{Aut}(Q)$ acts transitively on the set of ordered pairs $(x,y)$ with $Q=\langle x,y\rangle$ . In $F_p^k$ , the field of order $p^k$ , a choice of basis uniquely determines an element of $\mathrm{Aut}(F_p^k)=\mathrm{GL}(k,p)$ and vice versa, a well known fact from linear algebra. We say that $Q$ and $F_p^k$ are `homogeneous'. If $G$ is a $d$ generated group ($d$ minimal), we construct an extension $G(d)$ which is homogeneous and is the smallest such extension. These extensions have many interesting properties inherited from their base group and have wide applications in many (seemingly) different areas of mathematics.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
biddle at math dot binghamton dot edu

Classifying Conlon groups

JOSEPH PHILLIP BRENNAN, University of Florida

In 1949 George Szekeres presented a determination of finite $p$ -groups possessing an abelian maximal subgroup. Following Dr. Szekeres' construction, in 1974 Sam Conlon presented a classification of finite $p$ -groups possessing an abelian maximal subgroup which have cyclic centers, referred to here as Conlon groups. I will present a separate classification of Conlon groups.

UNIVERSITY OF FLORIDA
GAINESVILLE, FLORIDA
brennanj at ufl dot edu

Subgroups satisfying the Frattini Argument

BEN BREWSTER, Binghamton University

A subgroup $U$ of group $G$ satisfies the Frattini argument in $G$ provided that for normal subgroup $K$ of $G$ , $G = KL$ where $L$ is the normalizer of $U\cap K$ . One is acquainted with the fact that a Sylow subgroup of $G$ always satisfies the Frattini argument in $G$ . In a solvable group, any injector for a Fitting set satisfies the Frattini argument in $G$ as well. The nature of the subgroups which satisfy the Frattini argument will be probed in this talk.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
ben at math dot binghamton dot edu

Diameters of Brauer graphs in solvable groups

JAMES COSSEY, University of Akron

Let $B$ be a block of the solvable group $G$ , with defect group $D$ . Much is already known about the structure of $B$ if $D$ is known to be cyclic. In particular, the Brauer graph of $B$ has diameter 2. In this talk we examine the Brauer graph if $D$ is assumed to be abelian, and we give bounds on the diameter. We then extend these results to blocks with normal defect group. This is joint work with I.M. Isaacs and Mark Lewis.

UNIVERSITY OF AKRON
AKRON, OH
cossey at uakron dot edu

Interval enforceable properties of finite groups

WILLIAM JOSEPH DEMEO, University of Hawaii

What properties of a finite group can be inferred from the structure of an upper interval in its subgroup lattice? Suppose $P$ is a group property and suppose there exists a finite lattice $L$ such that if $G$ is a finite group with $L \cong \{K \mid H\leq K \leq G\}$ then $G$ has property $P$ . We call such a $P$ an interval enforceable (IE) property. We define two related notions, called core-free interval enforceable (cf-IE) and minimal interval enforceable (min-IE). The definitions are similar, but cf-IE requires that $H$ be a core-free subgroup of $G$ , while min-IE requires that $G$ have minimal order among groups which have $L$ as an upper interval in their subgroup lattices. If a group property is IE, then it is cf-IE, and if it is cf-IE, then it is min-IE. Proving that a given property is cf-IE is typically easier than proving that it is IE, but we give a simple sufficient condition under which the core-free hypothesis is superfluous. The fact that insolubility is a cf-IE property is well known, and we give an example of a finite lattice which proves this. Insolubility also satisfies the sufficient condition mentioned above, so it is IE. It is easy to see that solubility is not an IE property, and we prove that it also fails to be cf-IE by showing that a cf-IE property cannot preclude certain (insoluble) wreath product groups. We discuss some other properties which are known to be IE, cf-IE, or min-IE, and explain how these ideas relate the most important open problem in universal algebra - the finite lattice representation problem.

UNIVERSITY OF HAWAII
HONOLULU , HI
williamdemeo at gmail dot com

Generalizing $t$ -groups

ARNOLD D. FELDMAN, Franklin & Marshall College

A $t$ -group is a group in which normality is a transitive property. We look at various generalizations of $t$ -groups and provide some examples to distinguish among them.

FRANKLIN & MARSHALL COLLEGE
LANCASTER, PA
afeldman at fandm dot edu

Loops that are partitioned by groups

TUVAL FOGUEL, Western Carolina University

A set of subgroups of a group is said to be a partition if every nonidentity element belongs to one and only one subgroup in this set. The study of groups with partition dates back to a paper by Miller published in 1906. In this talk we will look at the structure of loops that are partitioned by subgroups.

WESTERN CAROLINA UNIVERSITY
CULLOWHEE, NC
tsfoguel at wcu dot edu

A duality for the algebra of conditional logic

FERNANDO GUZMAN, Binghamton University

We present a duality for the variety of algebras associated with the three-valued conditional logic. Conditional logic, provides the semantics for programming languages that use short-circuit evaluation. The dual category consists of Stone spaces with a lower bounded partial order. The duality is natural in the sense of Clark and Davey. This is joint work with Gina Kucinski.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
fer at math dot binghamton dot edu

A Construction of non-residually finite groups of intermediate growth

LAKHDAR HAMMOUDI, Ohio University

The purpose of this talk is to construct some finitely generated non-residually finite infinite $p$ -groups of intermediate growth. This provides, after Anna Erschler, another yet a different solution to Grigorchuk's problem.

OHIO UNIVERSITY
CHILLICOTHE, OHIO
hammoudi at ohio dot edu

A note on the representation theory of MV-algebras

MIKE HAMPTON, Binghamton University

It has recently been shown by Dubuc and Poveda [1] that every MV-algebra is isomorphic to the algebra of global sections on some sheaf space of MV-chains. In the paper, it is claimed that the functors sending MV-algebras to sheaf spaces and vice versa are adjoints. This claim is not needed for their main result. In this talk, we will produce a counterexample to this claim and a way to fix it.

1.

Eduardo J. Dubuc and Yuri A. Poveda, Representation theory of MV-algebras, Ann. Pure Appl. Logic 161 (2010), no. 8, 1024-1046.

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
hampton at math dot binghamton dot edu

Jacobi sum matrices

CHARLES SHANNON HOLMES, Miami University/Math Dept--retired

This abstract is an unsolicited ad for what I have found to be an excellent paper in the MATHEMATICS MONTHLY from February, 2012 by the same title. The author of that paper is Dr. Samuel K. Vandervelde, a number and graph theorist, who teaches at St. Lawrence University.

Any entry of a Jacobi sum matrix is a Jacobi sum. A Jacobi sum $J(\alpha,\beta)$ takes as its arguments a pair of multiplicative characters $\alpha$ , $\beta$ on a given finite field $F$ and yields a complex number, which is the result of a convoluted sum that resembles a dot product, so sum $J(\alpha,\beta) = \sum\alpha(f)\beta(1-f)$ , where the sum is over all elements of $F$ . The fact that the multiplicative group of $F$ is cyclic forces the characters $\alpha,\beta$ to be powers of one character, for which there are several possibilities. Pick one of these and call it the generating character. These powers for $\alpha$ and $\beta$ , say $i$ and $j$ , determine the $(i,j)$ entry in the Jacobi matrix $J$ .

Example. Let $F$ be $\mathbf{F}_5$ , the finite field with five elements, and take the generating character $\gamma$ to be determined by $\gamma(2) = i$ , the complex number. The matrix $J$ determined by this choice is the $4\times 4$ matrix

$$J = \left(\begin{array}{rccc} 3 & -1 & -1 & -1\\ -1 & -1-2i & ... ...1 & \hphantom{-}1-2i\\ -1 & \hphantom{-}1 & 1-2i & -1+2i \end{array}\right).$$

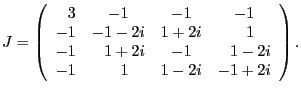
Any Jacobi matrix is symmetric and has determinant zero, as in this example.

Vandervelde's principal contribution to the topic of Jacobi sums is to use these Jacobi matrices to organize the properties of Jacobi sums, so that the eigenvalues and determinants encode many of the classical properties of Jacobi sums.

Most of my presentation will be devoted to selling Vandervelde's article by trying to make certain all in attendance understand the basics of Jacobi matrices. In other words this talk is mostly expository. There may be a moment or two at the end of the talk to call attention to a few corollaries beyond Vandervelde's article.

MIAMI UNIVERSITY/MATH DEPT--RETIRED
OXFORD, OHIO
holmescs at muohio dot edu

Localization, subnormal structure of classical groups

YOU HONG, Department of Mathematics, Suzhou University

Let $(R,\lambda)$ be a commutative form ring, and let $(J,\gamma)$ be a form ideal of $(R,\lambda)$ . Using principal localization and maximal localization staggered and some new results on localization-completion method in the past twenty years, we obtain a complete description of all subgroups of the generalized unitary group $\mathrm{U}_{2n}(R,\lambda)$ which are normalized by relative elementary subgroup $\mathrm{EU}_{2n}(J,\gamma)$ for all $n>3$ .

DEPARTMENT OF MATHEMATICS, SUZHOU UNIVERSITY
SUZHOU, JIANGSU, CHINA
youhong at suda dot edu dot cn

Group matrices and their applications

KENNETH W JOHNSON, Penn State Abington

Group representation theory came from the study of group matrices and their determinants. Given a finite group $G$ , a group matrix $X_{G}$ is a matrix encoding the operation of right division in $G$ in the following sense. If $% \{g_{1},\ldots,g_{n}\}$ are the elements of $G$ , a set $\{x_{g_{1}},\ldots,x_{g_{n}}\}$ of variables is taken and the $(i,j)^{\rm th}$ entry of $X_{G}$ is taken to be $x_{g_{i}g_{j}^{-1}}$ . For example the group matrix of the symmetric group $\mathcal{S}_{3}$ is

$$\left[ \begin{array}{cccccc} x_{1} & x_{3} & x_{2} & x_{4... ...x_{5} & x_{4} & x_{2} & x_{3} & x_{1}% \end{array}% \right]$$

where $x_{i}$ is used to abbrevate $x_{g_{1}}$ and the elements are listed in the order $e$ , $(123)$ , $(132)$ , $(12)$ , $(13)$ , $(23)$ .

A group matrix for $C_{n}$ with the elements listed as $% \{e,a,a^{2},\ldots,a^{n-1}\}$ is a circulant, i.e a matrix $% C(b_{1},\ldots,b_{n})$ whose first row is $[b_{1},\ldots,b_{n}]$ , with each subsequent row obtained from the previous one by shifting entries one place to the right and wrapping around. For example the group matrix for $C_{3}$ is

$$\left[ \begin{array}{ccc} x_{1} & x_{3} & x_{2} \\ x_{2... ... & x_{3} \\ x_{3} & x_{2} & x_{1}% \end{array}% \right] .$$

In joint work, Vojtechovsky and the presenter showed that given any group $G$ of order $mr$ with a cyclic subgroup $H$ of order $r$ , $X_{G}$ can be put in the form of an $m\times m$ block matrix all of whose blocks are $r\times r$ circulants. Subsequently, I have been able to show that if $H$ is an arbitrary subgroup of $G$ of order $r$ it is always possible to express $% X_{G}$ as an $m\times m$ block matrix all of whose blocks are of the form $% X_{H}(x_{g_{1}},\ldots,x_{g_{r}})$ where the $r$ -tuple of elements $% (g_{1},\ldots,g_{r})$ are in $G$ . Such matrices are more regular if $H$ is normal, of if $G$ is a product of two subgroups $G=HK$ with $H\cap K=\{e\}$ .

Group matrices have been used to obtain results on group rings, and appear in work on control theory, wavelets and Fourier analysis on finite groups. The above structure of $X_{G}$ can be used to efficiently diagonalise a group matrix.

The ``Tannaka-Krein'' duality for non-abelian groups may be stated in several ways, but it seems that the most effective version is given in terms of Hopf algebras. I will try to explain how group matrices may be used to create a category of representations and shed light on this duality.

PENN STATE ABINGTON
ABINGTON, PA
kwj1 at psu dot edu

Secret sharing scheme using group presentations and word problem

DELARAM KAHROBAEI, CUNY Graduate Center & NYCCT, CUNY, PhD Program in CS

A $(t,n)$ -threshold secret sharing scheme is a method to distribute a secret among $n$ participants in such a way that any $t$ participants can recover the secret, but no $t-1$ participants can. In this paper, we propose two secret sharing schemes using non-abelian groups. One scheme is the special case where all the participants must get together to recover the secret. The other one is a $(t,n)$ -threshold scheme that is a combination of Shamir's scheme and the group-theoretic scheme proposed in this talk.

CUNY GRADUATE CENTER & NYCCT, CUNY, PHD PROGRAM IN CS
NEW YORK, NY
dkahrobaei at gc dot cuny dot edu

On generalized 2-Baer groups

LUISE-CHARLOTTE KAPPE, Binghamton University

A group is called an $n$ -Baer group if all cyclic subgroups are $n$ -subnormal; and is called a generalized $n$ -Baer group if the subgroup generated by the cyclic subgroups which are not $n$ -subnormal is a proper subgroup of the group. The $1$ -Baer groups are the familiar Dedekind groups. Generalized $1$ -Baer groups, otherwise known as generalized Dedekind groups, have been extensively investigated by D. Cappitt, L.-C. Kappe, and D.M. Reboli. They have nilpotency class $2$ as well as cyclic commutator subgroup and the $2$ -generator groups among them have been classified.

By results of Heineken and Mahdiavanary, $2$ -Baer groups have nilpotency class $3$ and the $2$ -generator groups in this class have been classified. Our goal is to find out if there is a restriction on the nilpotency class of generalized $2$ -Baer groups. In addition, we are exploring whether there are any structural restrictions on this class of groups. We are currently in the process of classifying $2$ -generator $2$ -Baer groups.

This is joint work with Antonio Tortora of the University of Salerno.

BINGHAMTON UNIVERSITY
BINGHAMTON, NEW YORK
menger at math dot binghamton dot edu

The algebraic lattice of algebraic closure operators

MARTHA LEE HOLLIST KILPACK, Binghamton University

A closure operator on an infinte set $S$ is finitary or algebraic if for all $A\subseteq S$ , the closure of $A$ is equal to the union of the closures of the finite subsets of $A$ . I will show if we take the set of all algebraic closure operators on $S$ , it forms not only a lattice, but also an algebraic lattice.

BINGHAMTON UNIVERSITY
ENDWELL, NY
kilpack at math dot binghamton dot edu

Counting characters in blocks of solvable groups with abelian defect group

MARK L. LEWIS, Kent State University

If $G$ is a solvable group and $p$ is a prime, then the Fong-Swan Theorem shows that given any irreducible Brauer character $\varphi$ of $G$ , there exists a character $\chi \in {\rm Irr} (G)$ such that $\chi^o = \varphi$ , where ${}^o$ denotes the restriction of $\chi$ to the $p$ -regular elements of $G$ . We say that $\chi$ is a lift of $\varphi$ in this case. It is known that if $\varphi$ is in a block with abelian defect group $D$ , then the number of lifts of $\varphi$ is bounded above by $\vert D\vert$ . In this paper we give a necessary and sufficient condition for this bound to be achieved, in terms of local information in a subgroup $V$ determined by the block $B$ .

This is joint work with J. P. Cossey.

KENT STATE UNIVERSITY
KENT, OH
lewis at math dot kent dot edu

On $\Pi$ -property and $\Pi$ -normality of subgroups of finite groups

BAOJUN LI, School of Mathematics, Chengdu University of Information Technology, Visiting in WCU

Let $H$ be a subgroup of group $G$ . $H$ is said to satisfy the $\Pi$ -property in $G$ if $\vert G/K:N_{G/K}(HK/K\cap L/K)\vert$ is a $\pi\bigl((HK/K)\cap( L/K)\bigr)$ -number for any chief factor $L/K$ of $G$ , and, if there is a subnormal supplement $T$ of $H$ in $G$ such that $H\cap T\le I\le H$ for some subgroup $I$ satisfying the $\Pi$ -property in $G$ , then $H$ is said to be $\Pi$ -normal in $G$ . These properties are common properties of many known generalized permutabilities of subgroups. Groups can be described when some primary subgroups are $\Pi$ -normal, and many known results are generalized.

SCHOOL OF MATHEMATICS, CHENGDU UNIVERSITY OF INFORMATION TECHNOLOGY
CHENGDU, SICHUAN, CHINA
baojunli at cuit dot edu dot cn

Nonabelian tensor squares of nilpotent products of cyclic groups

ARTURO MAGIDIN, University of Louisiana at Lafayette

In 2008, R. Blyth, P. Moravec, and R.F. Morse proved that if $F(n,c)$ is the relatively free nilpotent group of class $c$ and rank $n$ , then its nonabelian tensor square is given by

$$F(n,c)\otimes F(n,c)\cong (F(n,c+1))'\times F^{\rm ab}_{\binom{n+1}{2}},$$

where $F^{\rm ab}_k$ is the free abelian group of rank $k$ ; they also determined the structure of $(F(m,c))'$ .

The group $F(n,c)$ is the $c$ -nilpotent product of $n$ copies of the infinite cyclic group. We consider extensions of the description above when we take $c$ -nilpotent products of cyclic groups in the ``small class'' case.

UNIVERSITY OF LOUISIANA AT LAFAYETTE
LAFAYETTE, LOUISIANA
magidin at member dot ams dot org

On bigenetic properties in groups

MAURIZIO MERIANO, Universitá Degli Studi di Salerno

A group-theoretical property $\mathcal{P}$ is said to be bigenetic if a group $G$ has property $\mathcal{P}$ , whenever all $2$ -generator subgroups of $G$ have property $\mathcal{P}$ . This terminology was introduced by J.C. Lennox in 1972. Commutativity and Engel conditions are examples of bigenetic properties. Surprisingly, in the class of all finite groups also nilpotency and solvability are bigenetic properties. The aim of this talk is essentially to illustrate some results which show how the structure of a group can be influenced by properties satisfied by its $2$ -generator subgroups. In particular, we investigate some conditions closely related to Engel conditions.

UNIVERSITÁ DEGLI STUDI DI SALERNO
FISCIANO, SALERNO, ITALY
mmeriano at unisa dot it

Whales and minnows and Galois groups

Dedicated to Professor T.-Y. Lam

JAN MINAC, Western University

Some Galois groups may seem so small that one expects little arithmetic information from them. Yet we shall see how such groups can encode valuations, orderings, and other important invariants of fields.

WESTERN UNIVERSITY (FORMERLY THE UNIVERSITY OF WESTERN ONTARIO)
LONDON , ONTARIO
jminac1811 at gmail dot com

Nilpotent subgroups of class $\leq 2$ of maximal order

ANNI NEUMANN, University of Tübingen

Let $G$ be a finite group. Denote by $\mathcal{A}_2(G)$ the set of all nilpotent subgroups of $G$ of class $\leq 2$ of maximal order. A quasisimple group is a perfect group $K$ such that $K/Z(K)$ is simple. A component of $G$ is a subnormal quasisimple subgroup.

In my work I have completely classified the action of elements of $\mathcal{A}_2(G)$ on the components of $G$ .

In my talk I will discuss the prominent subcase for components, which are Chevalley-groups in characteristic two. I will outline the proof of:

Theorem 1   Let $G$ be a finite group and $E$ a component of $G$ with $E/Z(E)$ isomorphic to a simple Chevalley-group in characteristic two where $E/Z(E)$ is not isomorphic to $\mathrm{PSL}(2,2^m)$ ($m \geq 2$ ), $\mathrm{Sp}(4,2)'$ if $2 \Big \vert \vert Z(E)\vert$ , $^2\!B_2(8)$
if $Z(E)\neq 1$ , $\mathrm{PSL}(3,4)$ if $Z(E)$ is a $2$ -group of exponent 4. Then $E$ is normalized by all $A \in \mathcal{A}_2(G)$ .

UNIVERSITY OF TÜBINGEN
TÜBINGEN, GERMANY
anni.neumann at acvan dot de

On a family of groups described by Nakajima and a counterexample by Stong

MARA D. NEUSEL, Texas Tech University

Subgroups of the general linear group $\mathrm{GL}(n, F)$ that are generated by pseudoreflections lead to rings of invariants that are polynomial, and conversely. Well, this result is true in the nonmodular case. In the modular case the classification of groups giving polynomial invariant rings has eluded us so far. In 1980 Nakajima considered modular representations of $p$ -groups. He identified the family of such groups leading to polynomial invariant rings. However his characterization is valid only over the prime field as a counterexample by Stong shows. We want to study Nakajima's family of groups a bit closer, and in particular want to show why Stong's counterexample must exit.

TEXAS TECH UNIVERSITY
LUBBOCK, TX
mara.d.neusel at ttu dot edu

Projective limits of finite permutation groups

PETER PLAUMANN, Department Mathematik, Universität Erlangen-Nürnberg

A transitive action of a group $G$ can be encoded by a triple ${\mathcal F}=\big(G,H,K\big)$ where $H$ is a subgroup of $G$ and $K$ is a set of coset representatives of $H$ in $G$ sucht that $1\in K$ . The action of $G$ is given by

$$(xH)\cdot g=(xg)H$$

for all $x\in K$ . Denoting by $x\circ g,\,x\in K, g\in G$ the representative of the coset $(xg)H$ the assignment

$$((x,g)\mapsto x\circ g):K\times G\to K$$

describes the given action of $G$ .

With the multiplication $\mu(x,y)=x\circ y$ the set $K$ is a left loop, that means:

a)

All equations $a\circ x=b$ have a unique solution.

b)

$1$ is a neutral element of $(K,\circ)$ .

We call ${\mathcal F}=\big(G,H,K\big)$ a left loop folder if the set $K$ generates $G$ .


Conversely, if $(L,\cdot)$ is a left loop we define

$$R_a=(x\mapsto x\cdot a):L\to L,$$

$${\sf TR}(L)=\{R_a \mid a\in L\},\quad {\sf RMult}(L)=\langle{\sf TR}(L)\rangle$$

and denote the stabilizer of $1$ in ${\sf RMult}(L)$ by ${\mathcal J}_r(L)$ .

Theorem 2   If $L$ is a left loop, then $\big({\sf RMult}(L),{\mathcal J}_r(L),{\sf TR}(L)\big)$ is a left loop folder.

An epimorphism $\eta:\big(G_1,H_1,K_1\big)\to\big(G_1,H_1,K_1\big)$ of left loop folders is a group epimorphism $\pi:G_1\to G_2$ satisfying $\pi(H_1)=H_2$ and $\pi(K_1)=K_2$ . Given a projective system

$$\Lambda=\Big(\big(G_\alpha,H_\alpha,K_\alpha\big),\pi_{\beta,\alpha}\Big)_{\beta>\alpha}$$

where the $\pi_{\beta,\alpha}$ are epimorphisms one can form without difficulties the projective limit.

Theorem 3   For a projective system $\Lambda$ of left loops the projective limit
$\Pi=\nobreak{\lim\limits_{\displaystyle\longleftarrow}}_{\alpha}\Lambda$ is a left loop folder. In particular $\Pi$ defines a compact, totally disconnected topological loop $L$ for which the group ${\sf RMult}(L)={\lim\limits_{\displaystyle\longleftarrow}}_{\alpha}{\sf RMult}(L_\alpha)$ is a profinite group.

Theorem is found in

W. HERFORT, P. PLAUMANN, Boolean and profinite loops, Topology Proceedings 7, 233-237 (2001).

The article cited is the base for further joint investigations on compact, totally disconnected loops together with W. Herfort (Vienna) and L. Sabinina (Cuernavaca, Mexico).

DEPARTMENT MATHEMATIK, UNIVERSITÄT ERLANGEN-NÜRNBERG
ERLANGEN,
peter.plaumann at mi dot uni-erlangen dot de

Cellular automata over non-abelian group alphabets

EIRINI POIMENIDOU, New College of Florida

In the study of cellular automata, one is interested in predicting the long term behavior of an automaton based on its local rules. In the classical case of additive cellular automata, one relies heavily on the fact that an update rule can be thought of as a group homomorphism. We develop new techniques to study the behavior of cellular automata over non-abelian groups. We develop necessary and sufficient conditions for a state to have a predecessor when the update rule is Wolfram's rule 90 over non abelian groups. We apply our methods to study the fraction of states that are reachable through evolution in automata over finite dihedral groups.

Joint work with Erin Craig.

NEW COLLEGE OF FLORIDA
SARASOTA, FL
poimendou at ncf dot edu

On the covering number of small symmetric groups

DANIELA NIKOLOVA POPOVA, Florida Atlantic University

Every group $G$ with a finite non-cyclic homomorphic image is a union of finitely many proper subgroups. The minimal number of subgroups needed to cover $G$ is called the covering number of $G$ , denoted by $\sigma(G)$ . Tomkinson showed that for a soluble group $G$ , $\sigma(G)= p^k+1$ , where $p$ is a prime, and he suggested the investigation of the covering number for families of finite non-soluble groups, in particular simple ones. For the symmetric groups $S_n$ Maroti recently showed that $\sigma(S_n) = 2^{n-1}$ if $n$ is odd unless $n = 9$ , and $\sigma(S_n)\leq 2^{n-2}$ if $n$ is even. We have determined the exact covering number of $S_n$ for some small values of $n$ , and found ranges for others.

Joint work with Luise-Charlotte Kappe, Binghamton University.

FLORIDA ATLANTIC UNIVERSITY
BOCA RATON, FL
dpopova at fau dot edu

Basic algebras of blocks of finite groups

LEE STEPHEN RANEY, University of Florida

Let $G$ be a finite group and let $F$ be an algebraically closed field of characteristic $p > 0$ . A block of $G$ is an indecomposable direct summand of the group algebra $FG$ . A block is then an algebra itself. One way to understand the representation theory of any finite dimensional $F$ -algebra $A$ is to understand its basic algebra. The basic algebra $B$ of $A$ is a (usually) less complicated algebra, and the representations of $B$ share many important properties with the representations of $A$ . We will discuss the definition of the basic algebra, techniques for calculating basic algebras of blocks of the group algebra $FG$ , and give some examples.

UNIVERSITY OF FLORIDA
GAINESVILLE, FLORIDA
raney at ufl dot edu

Multiplicities of faithful irreducible character degrees of subgroups of wreath product $p$ -groups

JEFFREY MARK RIEDL, University of Akron

Let $p$ be an odd prime, let $Z_p$ denote the cyclic group of order $p$ , and let $P$ denote the iterated regular wreath product group $Z_p\wr Z_p\wr Z_p$ , which has an easy-to-see normal subgroup $B$ that is elementary abelian of rank $p^2$ .

We have developed an algorithm for calculating the number of faithful irreducible ordinary characters of every degree for certain well-behaved subgroups of $P$ . This algorithm is computationally practical when the prime $p$ is small. We have successfully implemented this algorithm in the cases $p=3$ and $p=5$ for a particular collection of subgroups of $P$ which we denote by $H_{jk}$ , where the pair of indices $j$ and $k$ are integers ranging over $0\le j<p^{2}-p$ and $0\le k<p$ . We mention that $H_{jk}$ splits over its abelian normal subgroup $B\cap H_{jk}$ and that the indices $j$ and $k$ correspond to the facts $\vert B:B\cap H_{jk}\vert=p^{j}$ and $\vert H_{jk}:B\cap H_{jk}\vert=p^{p-1-k}$ . In the case $p=5$ our implementation involved the creation of an extensive and elaborate computer program.

In this talk we present the data that we have obtained using our implementation of the algorithm, namely the number of faithful irreducible characters of every degree for each of the groups $H_{jk}$ in the cases $p=3$ and $p=5$ .

Joint work with Dan Raies of the University of Akron.

UNIVERSITY OF AKRON
AKRON, OH
riedl at uakron dot edu

Groups with few isomorphism types of derived subgroup

DEREK SCOTT ROBINSON, University of Illinois at Urbana-Champaign

By a derived subgroup of a group G is meant the commutator subgroup of a subgroup of G. I will discuss the structure of groups in which the number of isomorphism types of derived subgroup is very small.

UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
URBANA, IL
dsrobins at illinois dot edu

Moufang loops of order 243

MICHAEL C SLATTERY, Marquette University

The talk will discuss the classification and some properties of non-associative Moufang Loops of order 243. There are 72 such loops and the list was produced by computer program.

MARQUETTE UNIVERSITY
MILWAUKEE, WI
mikes at mscs dot mu dot edu

A new "ZJ"-Theorem

RONALD MARK SOLOMON, The Ohio State University

Glauberman and I have discovered a new characteristic subgroup of a $p$ -stable group with properties analogous to those of $\mathrm{ZJ}(P)$ , but easier to prove. I will report on this.

THE OHIO STATE UNIVERSITY
COLUMBUS, OHIO
solomon.1 at osu dot edu

Locally $s$ -arc transitive graphs arising from the product action

ERIC ALLEN SWARTZ, Binghamton University

We will discuss the definition of locally $s$ -arc transitive graphs and methods used to study them, which are closely related to rank 2 amalgams of finite groups. An important subcase in this study arises when the automorphism group of the graph acts faithfully and quasiprimitively with type PA (product action) on two orbits of vertices. Recent and ongoing work will be discussed, in which the first (nontrivial) examples of these graphs with type PA have been constructed.

This is joint work with Michael Giudici (University of Western Australia).

BINGHAMTON UNIVERSITY
BINGHAMTON, NY
eswartz at math dot binghamton dot edu

Endoisomorphisms and correspondences of characters

ALEXANDRE TURULL, University of Florida

Endoisomorphisms provide a flexible and convenient way to describe character correspondences which commonly arise in the representation theory of finite groups.

Let $G_1$ , $G_2$ and $\overline{G}$ be finite groups, and let $\pi_1 : G_1 \to \overline{G}$ and $\pi_2 : G_2 \to \overline{G}$ be surjective group homomorphisms.

Let $R$ be a principal ideal domain, let $M_1$ be a finitely generated $RG_1$ -module and let $M_2$ be a finitely generated $RG_2$ -module. Many characters and Brauer characters of subgroups of $G_1$ are related to $M_1$ and many characters and Brauer characters of subgroups of $G_2$ are related to $M_2$ . An endoisomorphism relates $M_1$ and $M_2$ .

After discussing the definition of endoisomorphism, we will discuss how each endoisomophism provides a unique correspondence from the characters related $M_1$ to the characters related to $M_2$ , and some of the properties of this correspondence.

UNIVERSITY OF FLORIDA
GAINESVILLE, FLORIDA
turull at ufl dot edu

Cayley-Sudoku tables, loops, quasigroups, and more questions from undergraduate research

MICHAEL WARD, Western Oregon University

At the 2010 Ohio State-Denison Conference, we asked about a certain condition that arose in an undergraduate research project on Cayley-Sudoku tables. Loop theorists in attendance enthusiastically noted it was a rediscovery of a ``well-known'' 1939 theorem of R. Baer. In this talk, we will review the connection of Baer's Theorem to Cayley-Sukoku Tables and report on the ensuing search for new (in a sense to be described) examples of groups satisfying Baer's condition. A related mistake in the Latin square literature will be discussed. An inductive construction of Cayley-Sudoku tables will be presented along with (time permitting) a Magic Cayley-Sudoku table. In the hope that lightning will strike twice in the same place, the audience will once again be queried about connections with other well-known results.

WESTERN OREGON UNIVERSITY
MONMOUTH, OREGON
wardm at wou dot edu

Computing the Chermak-Delgado lattice of wreath products

ELIZABETH WILCOX, Colgate University

For a finite group $G$ and a subgroup $H$ of $G$ , the Chermak-Delgado measure of $H$ with respect to $G$ is $m_G(H) = \vert H\vert \vert C_G(H)\vert$ . If $M_G$ is the maximal Chermak-Delgado measure across all subgroups of $G$ then

$$\mathcal{C}\mathcal{D}(G) = \{ H \leq G \mid m_G(H) = M_G\}$$

is a sublattice within the lattice of all subgroups of $G$ . This Chermak-Delgado lattice of $G$ is a dual lattice with a unique maximal element and each of its members is actually subnormal in $G$ .

This talk will discuss recent results about computing the Chermak-Delgado lattice of wreath products, namely:

1. If $G = H \wr C_p$ with $\vert Z(H)\vert>2$ or $p>2$ then $\mathcal{C}\mathcal{D} (G)$ is precisely the Chermak-Delgado lattice of the base subgroup of $G$ ; and
2. if $G = H \wr C_2$ where $\vert Z(H)\vert=2$ and $H \in \mathcal{C}\mathcal{D} (H)$ then $G$ is in $\mathcal{C}\mathcal{D} (G)$ .

We'll discuss why these particular conditions are necessary and avenues for further investigation.

1. If $G =wr C_p$ with $\vert Z(H)\vert>2$ or $p>2$ then $\mathcal{C}\mathcal{D} (G)$ is precisely the Chermak-Delgado lattice of the base subgroup of $G$ ; and
2. if $G =wr C_2$ where $\vert Z(H)\vert=$ and $H \in \mathcal{C}\mathcal{D} (H)$ then $G$ is in $\mathcal{C}\mathcal{D} (G)$ .

We'll discuss why these particular conditions are necessary and avenues for further investigation.

COLGATE UNIVERSITY
HAMILTON, NY
ewilcox at colgate dot edu

All simple groups are characterized by their non-commuting graphs

ANDREW WOLDAR, Villanova University

A conjecture made by Abdollahi, Akbari, and Maimani asserts that two finite groups having the same non-commuting graph are isomorphic provided one of the groups is assumed non-abelian simple. The conjecture had been previously verified by Han, Chen, and Guo when the simple group is assumed to be sporadic, and by Abdollahi and Shahverdi when it is assumed alternating. Recently, Ron Solomon and the speaker treated the case when one group is assumed to be simple of Lie type, thus completing verification of the conjecture. In our talk, we discuss some of the more salient features of our proof.

VILLANOVA UNIVERSITY
VILLANOVA, PA
andrew.woldar at villanova dot edu

Blocks of small defect

YONG YANG, University of Wisconsin-Parkside

We show the following result. Let $G$ be a finite solvable group with $O_p(G)=1$ , $p \geq 5$ and $\vert G\vert _p=p^n$ , then $G$ contains a block of defect less or equal to $\lfloor \frac {3n} 5 \rfloor$ .

UNIVERSITY OF WISCONSIN-PARKSIDE
KENOSHA, WI
yangy at uwp dot edu