This is a brief survey on a concept called almost injectivity that has been studied mostly by Harada, and his collaborators. Baba introduced this concept as a dual to the concept of almost projectivity. In this survey, we state salient results by main contributors on this topic and some recent results by the authors. This exposition is not claimed to be exhaustive but is meant to highlight important discoveries made in the area and to point out future possible work. A list of open questions is given. The interested readers, particularly graduate students would benefit most by going over the wealth of information contained in the referenced articles on almost injectivity and projectivity (Joint with S. K. Jain, Ohio University and King Abdulaziz University)
KING ABDULAZIZ UNIVERSITY
JEDDAH, SAUDI ARABIA
adelnife2 at yahoo dot com
We introduce a generalization of extending (CS) modules by using the concept of
![]() -large submodule which was defined in [1]. We give some properties of
this class of modules and study their relationship with the familiar concepts of
-large submodule which was defined in [1]. We give some properties of
this class of modules and study their relationship with the familiar concepts of
![]() -closed,
-closed, ![]() -complement submodules and the other generalization of
extending modules (
-complement submodules and the other generalization of
extending modules (![]() -complemented,
-complemented, ![]() -CS, s-
-CS, s-![]() -CS modules). We
are also interested in determining when a
-CS modules). We
are also interested in determining when a ![]() -divisible module is
-divisible module is
![]() -extending. For a
-extending. For a ![]() -extending module M with C3, we obtain a
decomposition theorem that there is a submodule K of M such that M=??? and K is
-extending module M with C3, we obtain a
decomposition theorem that there is a submodule K of M such that M=??? and K is
![]() (M)-injective. We also treat when a direct sum of -extending modules is
(M)-injective. We also treat when a direct sum of -extending modules is
![]() -extending.
Keywords:
-extending.
Keywords: ![]() -large submodule,
-large submodule, ![]() -closed submodule, extending module,
-closed submodule, extending module,
![]() -complemented module,
-complemented module, ![]() -CS module.
-CS module.
References [1]-Gomez Pardo, J. L. (1985). Spectral Gabriel Topologies and Relative Singular Functors. Communications in Algebra. 13 (1): 21-57.
ANTALYA, TURKEY
alkan at akdeniz dot edu dot tr
We consider only associative right and left artinian rings with identity. A chain ring is a ring whose left (right) ideals form a chain. Let R be a ring, then R is a local principal ring if and only if it is a chain ring. The motivation for the increased interest in chain rings is the recent use of finite chain rings in coding theory. We associate with each finite (artinian) chain ring six invariants(integers) and determine the number of isomorphism classes of chain rings with given invariants in terms of the number of commutative chain rings. Also we determine the enumeration of finite and artinian chain rings under some suitable conditions.
KING SAUD UNIVERSITY
RIYADH, SAUDI ARABIA
ykhamees at gmail dot com
Let ![]() be a finite graph and let
be a finite graph and let
![]() denote the
Leavitt path algebra. Let
denote the
Leavitt path algebra. Let
![]() and
and
![]() be two
cycles. We write
be two
cycles. We write
![]() if there is a
path that starts from
if there is a
path that starts from
![]() and finishes at
and finishes at
![]() .
Clearly, under the hypothesis that no two cycles have a common vertex, if
.
Clearly, under the hypothesis that no two cycles have a common vertex, if
![]() and
and
![]() then
then
![]() If
If ![]() ,
, ![]() ,.....,
,.....,![]() are distinct cycles and
are distinct cycles and
![]() .....
.....
![]() then we call this a chain of
length
then we call this a chain of
length ![]() We say a chain has an exit if
We say a chain has an exit if ![]() has an exit. Let
has an exit. Let ![]() be
a maximal length of a chain of cycles with an exit and let
be
a maximal length of a chain of cycles with an exit and let ![]() be a
maximal length of a chain of cycles without an exit.
be a
maximal length of a chain of cycles without an exit.
Theorem 1. ![]()
![]()
![]() is finite if and only if no
two different cycles have a common vertex.
is finite if and only if no
two different cycles have a common vertex.
Theorem 2. ![]()
![]()
![]() =
=
![]() or
or ![]()
(joint work with Adel Alahmadi, S. K. Jain and Efim Zelmanov)
KING ABDULAZIZ UNIVERSITY
JEDDAH, MEKKAH, SAUDI ARABIA
hamed9 at hotmail dot com
Let ![]() be a group of order
be a group of order ![]() (
(![]() need not be abelian, but we write
need not be abelian, but we write ![]() additively). An
additively). An
![]() matrix
matrix
![]() indexed by the elements of the
group
indexed by the elements of the
group ![]() (so
(so ![]() and
and ![]() belong to
belong to ![]() ) is said to be
) is said to be ![]() -developed (or
-developed (or
![]() -invariant) if it satisfies the condition
-invariant) if it satisfies the condition
![]() for all
for all
![]() .
.
![]() is said to be circulant if the underlying group
is said to be circulant if the underlying group ![]() is cyclic. Thus the
matrix
is cyclic. Thus the
matrix ![]() is completely determined by its first row.
Let RG denote the group ring of a given group G over a ring R. Then the set
of G-invariant matrices with entries from R is isomorphic to the group ring RG.
We report on some recent results on the following classes of objects that arise
from group invariant matrices: Group weighing matrices and perfect arrays with
complex roots of unity as its entries and sequences with ideal autocorrelations.
is completely determined by its first row.
Let RG denote the group ring of a given group G over a ring R. Then the set
of G-invariant matrices with entries from R is isomorphic to the group ring RG.
We report on some recent results on the following classes of objects that arise
from group invariant matrices: Group weighing matrices and perfect arrays with
complex roots of unity as its entries and sequences with ideal autocorrelations.
WRIGHT STATE UNIVERSITY
DAYTON, OH
k.arasu at wright dot edu
Skew cyclic codes, also called ![]() -cyclic codes, are a recently introduced
generalization of ordinary cyclic codes. Unlike most other codes related to
cyclic codes, one needs to work in the unfamiliar territory (for a coding
theorist!) of the non-commutative ring of skew polynomial ring over a field
which does not possess the unique factorization property. There have been useful
results and new codes obtained from this class of codes and their
generalizations. This talk will give an overview of recent results in the field.
-cyclic codes, are a recently introduced
generalization of ordinary cyclic codes. Unlike most other codes related to
cyclic codes, one needs to work in the unfamiliar territory (for a coding
theorist!) of the non-commutative ring of skew polynomial ring over a field
which does not possess the unique factorization property. There have been useful
results and new codes obtained from this class of codes and their
generalizations. This talk will give an overview of recent results in the field.
KENYON COLLEGE
GAMBIER, OH
aydinn at kenyon dot edu
In a recent paper of Alahmadi, Alkan and López-Permouth, a ring ![]() is
defined to have no simple middle class if the injectivity domain of any
simple
is
defined to have no simple middle class if the injectivity domain of any
simple
![]() -module is the smallest or largest possible. In this talk, we discuss some
properties of rings with no simple middle class. It is shown that if
-module is the smallest or largest possible. In this talk, we discuss some
properties of rings with no simple middle class. It is shown that if ![]() is a
right Artinian ring, then
is a
right Artinian ring, then ![]() has no simple middle
class if and only if there is a ring decomposition
has no simple middle
class if and only if there is a ring decomposition
![]() , where
, where ![]() is semisimple Artinian and
is semisimple Artinian and ![]() is zero or has one of the following
properties:
is zero or has one of the following
properties:
![]()
![]() is a right
is a right ![]() -ring with homogeneous right socle.
-ring with homogeneous right socle.
![]()
![]() has a unique noninjective simple right
has a unique noninjective simple right ![]() -module up to
isomorphism, and the right socle of
-module up to
isomorphism, and the right socle of ![]() is (homogeneous) singular.
is (homogeneous) singular.
Furthermore, if ![]() is a commutative Noetherian ring, then
is a commutative Noetherian ring, then ![]() has no simple
middle
class if and only if there is a ring decomposition
has no simple
middle
class if and only if there is a ring decomposition ![]() , where
, where ![]() is semisimple Artinian and
is semisimple Artinian and ![]() is a local ring.
is a local ring.
(This is a joint work with Bülent Saraç).
HACETTEPE UNIVERSITY
ANKARA, TURKEY
paydogdu at hacettepe dot edu dot tr
We provide constructions of cyclic 2-class Partially Balanced Incomplete Block Designs using cyclotomy in finite fields. Our results give theoretical explanation of the two sporadic examples given by Agrawal (1987). This is a joint work with K.T.Arasu and Cody Watson.
INDIAN INSTITUTE OF TECHNOLOGY GUWAHATI
GUWAHATI, ASSAM, INDIA
bpradeep20 at gmail dot com
Let R be a commutative ring and M an unital R-module. M is called co-Hopfian if any injective endomorphism of M is an isomorphism. M is called weakly co-Hopfian if any injective endomorphism of M is essential. The ring R is called weakly FC-ring if any weakly co-Hopfian R-module if finitely cogenerated. In this paper, we show that for a commutative ring R, the following conditions are equivalent : 1 - R is a weakly FC-ring. 2 - R is an Artinian principal ideal ring. Definitions and notations used in this paper can be found in [1] and [10]. Keywords: weakly FC-ring, Artinian principal ideal ring, finitely generated module, finitely cogenerated module, co-Hopfian module, weakly co-Hopfian module, uniform dimension.
References
[1] F. W. Anderson and K. R. Fuller : Rings and categories of modules, New York Springer-Verlag, Berlin, 1973. [2] SH. Asgary On weakly co-Hopfian modules. Bulletin of Iranian Mathematical Society. Vol. 33 N 1 (2007) pp. 65 - 72. [3] Barry, M. Diankha, O., Sangharé, M. : On commutative FGI-rings. Math. Sc. Res. J.9 (4) (2005) 87 - 91. [4] Barry, M., P.C. Diop :Some properties related to commutative weakly FGI-rings, J P Journal of Algebra, Number Theory and application Vol.19, issue 2,(2010) 141-153. [5] I. S. Cohen : On the structure and ideal theory of complete local rings, Trans. Amer. Soc., 59 (1946), 54 - 106. [6] I. S. Cohen, I. Kaplansky : Ring for which every module is a direct sum of cyclic modules, Math. Zeitschr Bd., 54(H2S), 97 - 101. [7] N.V. Dung, D.V. Huynh, P.F. Smith and R. Wisbauer : Extending Modules, Longman : Burnt Mill, 1994. [8] A. Haghany, M. R. Vedadi : Modules whose injective endomorphism are essential. J. Algebra 243 (2001) 765 - 779. [9] M. A. Kaïdi, M. Sangharé : Une caractérisation des anneaux artiniens à idéaux principaux in L.N.M., vol. 1328, Springer-Verlag, Berlin, 1988, 245 - 254. [10] T. Y. Lam : Lectures on modules and rings. G. T. M. (189), Springer- Verlag. Berlin-Heidelberg, New York(1999). [11] Sharpe, D.W. and Vamos, P. : Injective modules. Cambridge University Presss (1972). [12] W. V. Vasconscelos : On finitely generated flat modules. Proc. Am. Math. Soc. 138 (1969) 900 - 901. [13] W. V. Vasconscelos : Injective endomorphism of finitely generated modules. Proc. Am. Math. Soc. 25(1970) 505 - 512.
CHEIKH ANTA DIOP UNIVERSITY DAKAR ( SENEGAL )
DAKAR, SENEGAL
mansabadion1 at hotmail dot com
Eggert's Conjecture says that if one applies to a finite-dimensional
nilpotent commutative algebra ![]() over a perfect field of
characteristic
over a perfect field of
characteristic ![]() the
the ![]() -th-power map, then the dimension of the
algebra will shrink by a factor of at least
-th-power map, then the dimension of the
algebra will shrink by a factor of at least ![]() . Whether this elementary
statement is true is not known! I will motivate the conjecture, and
discuss versions of it that are not limited to prime characteristic
and/or to commutative
. Whether this elementary
statement is true is not known! I will motivate the conjecture, and
discuss versions of it that are not limited to prime characteristic
and/or to commutative ![]() , consequences it would have for finite
semigroups, and some examples.
, consequences it would have for finite
semigroups, and some examples.
UNIVERSITY OF CALIFORNIA, BERKELEY
BERKELEY, CALIFORNIA
gbergman at math dot berkeley dot edu
Let C be a subset of the set of all submodules of a module M. We say M is
"C-extending" if every element of C is essential in a direct summand of M. When
H is a nonempty subset of
![]() and C is the set of submodules of M which are invariant with respect
to H, we say M is HI-extending. The C-extending and HI-extending conditions are
investigated with respect to forming direct sums, direct summands, and dense
extensions. Applications are made when H is the set of all idempotents of
and C is the set of submodules of M which are invariant with respect
to H, we say M is HI-extending. The C-extending and HI-extending conditions are
investigated with respect to forming direct sums, direct summands, and dense
extensions. Applications are made when H is the set of all idempotents of
![]() , then C is the set of projective invariant submodules of M. The
projective invariant extending Abelian groups are characterized. Examples are
presented to illustrate and delimit our results. (This is joint work with Adnan
Tercan and Canan C. Yucel).
, then C is the set of projective invariant submodules of M. The
projective invariant extending Abelian groups are characterized. Examples are
presented to illustrate and delimit our results. (This is joint work with Adnan
Tercan and Canan C. Yucel).
UNIVERSITY OF LOUISIANA AT LAFAYETTE
LAFAYETTE, LA
gfb1127 at louisiana dot edu
Let ![]() be a ring with unity and
be a ring with unity and ![]() its group of units.
Let
its group of units.
Let
be the
be the
The investigation of the ![]() -radical
-radical ![]() and the
and the
![]() -subring
-subring
![]() was proposed by
H. Zassenhaus (see S. K. Sehgal and H. Zassenhaus, On the supercentre of a
group and its ring theoretic generalization, In Integral representations
and applications (Oberwolfach, 1980), volume 882 of Lecture Notes in
Math., pages 117-144. Springer, Berlin, 1981; S. K. Sehgal and H. J.
Zassenhaus, Group rings whose units form an FC-group, Math. Z.,
153(1):29-35, 1977.) They described the
was proposed by
H. Zassenhaus (see S. K. Sehgal and H. Zassenhaus, On the supercentre of a
group and its ring theoretic generalization, In Integral representations
and applications (Oberwolfach, 1980), volume 882 of Lecture Notes in
Math., pages 117-144. Springer, Berlin, 1981; S. K. Sehgal and H. J.
Zassenhaus, Group rings whose units form an FC-group, Math. Z.,
153(1):29-35, 1977.) They described the
![]() -subring of
-subring of
![]() -order as a unital ring with a finite
-order as a unital ring with a finite
![]() -basis
and a semisimple quotient ring.
-basis
and a semisimple quotient ring.
An infinite subgroup ![]() of
of ![]() is said to be an
is said to be an
![]() -subgroup if the left annihilator of each nonzero Lie
commmutator
-subgroup if the left annihilator of each nonzero Lie
commmutator ![]() in
in ![]() contains only finite
number of elements of the form
contains only finite
number of elements of the form ![]() , where
, where ![]() and
and ![]() .
In the case when
.
In the case when ![]() is an algebra over a field
is an algebra over a field ![]() , and
, and ![]() contains an
contains an ![]() -subgroup, we describe (see V. Bovdi, On elements in
algebras having finite number of conjugates, Publ. Math. Debrecen,
57(1-2):231-239, 2000) its
-subgroup, we describe (see V. Bovdi, On elements in
algebras having finite number of conjugates, Publ. Math. Debrecen,
57(1-2):231-239, 2000) its ![]() -subalgebra and the
-subalgebra and the ![]() -radical. This result
is an extension of V. Bovdi, Twisted group rings whose units form an
-radical. This result
is an extension of V. Bovdi, Twisted group rings whose units form an
![]() -group, Canad. J. Math., 47(2):274-289, 1995; G. H. Cliff and S. K.
Sehgal, Group rings whose units form an
-group, Canad. J. Math., 47(2):274-289, 1995; G. H. Cliff and S. K.
Sehgal, Group rings whose units form an ![]() -group, Math. Z.,
161(2):163-168, 1978; S. K. Sehgal and H. Zassenhaus, On the supercentre of a
group and its ring theoretic generalization, In Integral representations
and applications (Oberwolfach, 1980), volume 882 of Lecture Notes in
Math., pages 117-144. Springer, Berlin, 1981; S. K. Sehgal and H. J.
Zassenhaus, Group rings whose units form an FC-group, Math. Z.,
153(1):29-35, 1977.)
-group, Math. Z.,
161(2):163-168, 1978; S. K. Sehgal and H. Zassenhaus, On the supercentre of a
group and its ring theoretic generalization, In Integral representations
and applications (Oberwolfach, 1980), volume 882 of Lecture Notes in
Math., pages 117-144. Springer, Berlin, 1981; S. K. Sehgal and H. J.
Zassenhaus, Group rings whose units form an FC-group, Math. Z.,
153(1):29-35, 1977.)
UNIVERSITY OF DEBRECEN
DEBRECEN,
vbovdi at gmail dot com
The purpose of this short talk is to raise a question. S is the nxn matrix ring
over a field C Background:
1. Fitting;s Lemma asserts that every element in S is a sum of a unit and an
idempotent that commute.
2. Let X be the 0,1 diagonal matrices, a straigtforward determinant induction
argument shows that given a matrix M, one may subtract an element in X from M to
obtain a unit. X is thus an "adequate" set of idempotents.
Question, is it the case that every adequate set of idemotents must have n
choose k idempotents of rank k. In particular must an adequate set have ![]() elements. The REU's have proved this up to n=
elements. The REU's have proved this up to n=
U OF IOWA
IOWA CITY, IA
camillo at math dot uiowa dot edu
We will briefly discuss some questions on additive commutators in associative rings. In particular, a solution of a problem by Herstein on commutators and nilpotent elements in simple rings (joint work with E.R. Puczylowski and P.-H. Lee) will be presented.
KENT STATE UNIVERSITY
KENT, OH
chebotar at math dot kent dot edu
Motivated by results about an element of a ring that admits a spectral
idempotent (so-called a quasipolar element in literature), we introduce notions
of pseudopolar rings and quasipolar rings. A ring ![]() is called quasipolar if
every element of
is called quasipolar if
every element of ![]() is quasipolar (or, every element of
is quasipolar (or, every element of ![]() has a generalized
Drazin inverse). It is proved that strongly
has a generalized
Drazin inverse). It is proved that strongly ![]() -regular rings and uniquely
strongly clean rings are pseudopolar, pseudopolar rings are quasipolar, and
quasipolar rings are strongly clean. In this talk, we present Cline's formula
and Jacobson's lemma for the generalized Drazin inverse. The quasipolarity and
pseudopolarity of matrix rings and the triangular matrix rings over local rings
are also considered.
-regular rings and uniquely
strongly clean rings are pseudopolar, pseudopolar rings are quasipolar, and
quasipolar rings are strongly clean. In this talk, we present Cline's formula
and Jacobson's lemma for the generalized Drazin inverse. The quasipolarity and
pseudopolarity of matrix rings and the triangular matrix rings over local rings
are also considered.
DEPARTMENT OF MATHEMATICS, SOUTHEAST UNIVERSITY
NANJING, JIANGSU PROVINCE
jlchen at seu dot edu dot cn
We introduce the concept of a Galois covering of a pointed coalgebra. By an analog of a fundamental result of Gabriel, a pointed coalgebra embeds into the path coalgebra of its quiver. Topological coverings of quivers are used to construct covering coalgebras, including a universal covering for a path subcoalgebra of the path coalgebra. The theory developed shows that Galois coverings of coalgebras can be expressed by smash coproducts using the coaction of the automorphism group of the covering. Thus the theory of Galois coverings of pointed coalgebras is seen to be equivalent to group gradings of coalgebras, and representations of coverings are equivalent to graded comodules. Gradings in connection to coverings of quivers and representation theory were studied in the 80's by Green, Martinez-de la Pena, Bongartz and Gabriel, Riedtman, and recently for k-categories by Cibils and Marcos. One feature of the coalgebra theory is that neither the grading group nor the quiver is assumed finite in order to obtain a smash product coalgebra.
DEPAUL UNIVERSITY
CHICAGO, IL
wchin at condor dot depaul dot edu
In the commutative setting, many nice properties of a ring pass to its classical ring of quotients. In the noncommutative case, however, the situation is not nearly as nice. In this talk, we will focus on properties concerning zero-divisors, and we will present several constructions to illustrate the degree to which such properties pass from an Ore ring to its classical ring of quotients. This is joint work with C.Y. Hong, N.K. Kim and P.P. Nielsen.
WELLESLEY COLLEGE
WELLESLEY, MA
adiesl at wellesley dot edu
R. Dimitric gave an exhaustive characterization of slender objects in (Abelian) categories in early 1980's and subsequently. This work is given in considerable generality and as such may have not been understood well, so much so, that "rediscoveries" of partial results of this characterization seem to appear at steady rate. In this talk, I will give a few corollaries to my work, and especially in ring and module theory.
CUNY
NEW YORK, NY
RDIMITRIC at JUNO dot COM
We study torsionfree and divisible dimensions in terms of right derived functors
of ![]() . We also investigate the cotorsion pair cogenerated by the class
of cyclic torsionfree right
. We also investigate the cotorsion pair cogenerated by the class
of cyclic torsionfree right ![]() -modules. As applications, some new
characterizations of von Neumann regular rings,
-modules. As applications, some new
characterizations of von Neumann regular rings, ![]() -rings and semisimple
Artinian rings are
given. This talk is a report on joint work with Jiangsheng Hu.
-rings and semisimple
Artinian rings are
given. This talk is a report on joint work with Jiangsheng Hu.
DEPARTMENT OF MATHEMATICS, NANJING UNIVERSITY
NANJING, JIANGSU PROVINCE, CHINA
nqding at nju dot edu dot cn
The class of constacyclic codes plays a very significant role in the theory of
error-correcting codes. In this talk, we consider repeated-root codes of prime
power length over a class of finite chain rings, namely,
![]() , where
, where ![]() is any prime. All constacyclic codes of
length
is any prime. All constacyclic codes of
length ![]() over the ring
over the ring ![]() are studied. The units of the chain ring
are studied. The units of the chain ring
![]() are of the forms
are of the forms ![]() , and
, and
![]() , where
, where
![]() are nonzero elements of the Galois field
are nonzero elements of the Galois field
![]() , which
provides
, which
provides
![]() such constacyclic codes. First, the structure and Hamming
distances of all constacyclic codes of length
such constacyclic codes. First, the structure and Hamming
distances of all constacyclic codes of length ![]() over the finite field
over the finite field
![]() are obtained, and used as a tool to establish the structure
and Hamming distances of all
are obtained, and used as a tool to establish the structure
and Hamming distances of all
![]() -constacyclic codes of length
-constacyclic codes of length
![]() over
over ![]() . We then classify all cyclic codes of length
. We then classify all cyclic codes of length ![]() over
over
![]() , and obtain the number of codewords in each of those cyclic codes.
Finally, an
one-to-one correspondence between cyclic and
, and obtain the number of codewords in each of those cyclic codes.
Finally, an
one-to-one correspondence between cyclic and ![]() -constacyclic codes of
length
-constacyclic codes of
length ![]() over
over ![]() is constructed via a ring isomorphism, that carries
over the results about cyclic codes correspondingly to
is constructed via a ring isomorphism, that carries
over the results about cyclic codes correspondingly to ![]() -constacyclic
codes of length
-constacyclic
codes of length ![]() over
over ![]() .
.
DEPARTMENT OF MATHEMATICAL SCIENCES, KENT STATE UNIVERSITY.
WARREN, OHIO
hdinh at kent dot edu
A ring ![]() is called left pure semisimple if every left
is called left pure semisimple if every left ![]() -module is a direct
sum of finitely generated modules, or equivalently, every left
-module is a direct
sum of finitely generated modules, or equivalently, every left ![]() -module is
pure-injective. It is still an open problem whether left pure semisimple rings
always have finite representation type, known as the Pure Semisimplicity
Conjecture. It is known that this conjecture can be reduced to the hereditary
case. In this talk, we discuss some recent results on left pure semisimple
hereditary rings. We describe the distribution of indecomposable left
-module is
pure-injective. It is still an open problem whether left pure semisimple rings
always have finite representation type, known as the Pure Semisimplicity
Conjecture. It is known that this conjecture can be reduced to the hereditary
case. In this talk, we discuss some recent results on left pure semisimple
hereditary rings. We describe the distribution of indecomposable left
![]() -modules over such a ring
-modules over such a ring ![]() . We show, in particular, that every left pure
semisimple hereditary ring has tame representation type, in the sense that for
every natural number
. We show, in particular, that every left pure
semisimple hereditary ring has tame representation type, in the sense that for
every natural number ![]() , there are only finitely many non-isomorphic
indecomposable left
, there are only finitely many non-isomorphic
indecomposable left ![]() -modules that belong to the Ziegler closure of the
(finite) family of indecomposable left
-modules that belong to the Ziegler closure of the
(finite) family of indecomposable left ![]() -modules of length
-modules of length ![]() . (This is joint
work with José Luis García, University of Murcia, Spain)
. (This is joint
work with José Luis García, University of Murcia, Spain)
OHIO UNIVERSITY, ZANESVILLE CAMPUS
ZANESVILLE, OHIO
nguyend2 at ohio dot edu
Descent of a property of modules is a fundamental question in algebraic geometry when defining new classes of quasi-coherent sheaves. This means that the property can be defined using an open affine covering of the scheme. In the talk we will give an overview of the problem of descent with respect to several classes of modules that have been recently considered in [D,EGPT] to define a notion of (infinite dimensional) vector bundles.
The talk is part of a joint work with Pedro A. Guil Asensio and Jan Trlifaj.
References:
[D] V. DRINFELD, Infinite-dimensional vector bundles in algebraic geometry: an introduction, in The Unity of Mathematics, Birkhäuser, Boston 2006, pp. 263-304.
[EGPT] S. ESTRADA, P. GUIL ASENSIO, M. PREST, J. TRLIFAJ, Model category structures arising from Drinfeld vector bundles, preprint, arXiv:0906.5213.
UNIVERSIDAD DE MURCIA
MURCIA, SPAIN
sestrada at um dot es
We say that an additive functor
![]() between preadditive categories
between preadditive categories
![]() and
and ![]() is a local functor if, for every morphism
is a local functor if, for every morphism
![]() in
in
![]() ,
, ![]() isomorphism in
isomorphism in ![]() implies
implies ![]() isomorphism in
isomorphism in ![]() . In this talk, we
will show that there exists a number of pairs
. In this talk, we
will show that there exists a number of pairs
![]() of ideals of
of ideals of ![]() for
which the canonical functor
for
which the canonical functor
![]() is a local functor. These
pairs of ideals arise in a very natural way. Our main case will be when
is a local functor. These
pairs of ideals arise in a very natural way. Our main case will be when ![]() is
the category Mod-
is
the category Mod-![]() of all right modules over a ring
of all right modules over a ring ![]() , or some other
category strictly related to Mod-
, or some other
category strictly related to Mod-![]() , like the full subcategory mod-
, like the full subcategory mod-![]() of all
finitely presented
of all
finitely presented ![]() -modules, or the full subcategory of Mod-
-modules, or the full subcategory of Mod-![]() whose objects
are all
whose objects
are all ![]() -modules with a projective cover.
-modules with a projective cover.
UNIVERSITY OF PADOVA, ITALY
PADOVA, ITALY
facchini at math dot unipd dot it
An algebra is essentially regular of dimension ![]() if its homogenization is an
Artin-Schelter regular algebra of dimension
if its homogenization is an
Artin-Schelter regular algebra of dimension ![]() . We present a modified version
of matrix congruence which can be used to classify algebras defined by
generators and relations. This method can can be used to classify all
2-dimensional essentially regular algebras up to
. We present a modified version
of matrix congruence which can be used to classify algebras defined by
generators and relations. This method can can be used to classify all
2-dimensional essentially regular algebras up to
![]() -algebra
isomorphism. We give this classification, along with that of the corresponding
homogenized algebras.
-algebra
isomorphism. We give this classification, along with that of the corresponding
homogenized algebras.
UNIVERSITY OF WISCONSIN - MILWAUKEE
MILWAUKEE, WI
jdgaddis at uwm dot edu
The theme of the talk is aspects of quantum groups from a ring theoretic perspective. This will be discussed in terms of one particular example, quantum matrices - more accurately, the quantized coordinate rings of matrix varieties. These algebras will be introduced, their somewhat strange-looking relations will be motivated, and various properties will be discussed. Some of the surprising parallels between these algebras and the corresponding classical coordinate rings will be presented.
UNIVERSITY OF CALIFORNIA
SANTA BARBARA, CA
goodearl at math dot ucsb dot edu
We show that a morphism in a locally finitely presented Grothendieck category C is phantom if and only if it is Ext-orthogonal to the class of pure-injective objects. The ideal of morphisms that are orthogonal to phantom morphisms is also studied. When the category C has enough projectives, this ideal consists of all morphisms that factor through a pureinjective objects. The existence of pre-envelopes with respect to this ideal of the category is also proved. Finally, it is shown that the class of pureinjective objects is the closure under extensions of the class of pure-injective objects. We also outline how to extend these results to exact categories.
Joint work with X. Fu, I. Herzog and B. Torrecillas.
UNIVERSITY OF MURCIA
MURCIA, SPAIN
paguil at um dot es
For any countable, column finite, idempotent matrix ![]() with entries in a ring
with entries in a ring
![]() we will describe how to construct a couple of sequences of ideals of
we will describe how to construct a couple of sequences of ideals of ![]() that give some information on the countable generated projective module
determined by
that give some information on the countable generated projective module
determined by ![]() .
.
I want to explain that for some classes of rings (e.g. semilocal noetherian rings) this information, combined with some realization methods, is enough to determine all projective modules over them. For some other classes of rings (e.g. general semilocal rings) this seems to be the starting point of a, surprisingly rich, theory of countably generated projective modules.
The talk is based on joint work with P. Prihoda.
UNIVERSITAT AUTONOMA DE BARCELONA
BELLATERRA , BARCELONA, SPAIN
dolors at mat dot uab dot cat
Using the notion of relative projectivity, projective modules may be thought of as being those which are projective relative to all others. In contrast, a module M is said to be projectively poor if it is projective relative only to semisimple modules. We prove that all rings have projectively poor modules. In fact, every ring even has a semisimple projectively poor module.
We consider rings over which modules are either projective or projectively poor
and call them rings without a p-middle class.
As we analyze the structure of rings with no right p-middle class, among other
results, we show that any such ring is the ring
direct sum of a semisimple artinian ring and a ring K which is either zero or an
indecomposable ring such that either
(i) K is a semiprimary right SI-ring with non-zero radical, or
(ii) K is a semiprimary ring with right
![]() ,or
(iii) K is a prime ring with right Soc(K) = 0, and either J(K) = 0 or K J(K) and
J(K)K are infinitely generated, or
(iv) K is a prime right SI-ring with infinitely generated right socle.
For a partial converse, we also give examples of rings with no p-middle class of
types (i), (ii) and (iii).
(Joint works with Sergio R. Lopez-Permouth and Nil Orhan-Ertas, as well as Hai
Q. Dinh and Dinh van Huynh.)
,or
(iii) K is a prime ring with right Soc(K) = 0, and either J(K) = 0 or K J(K) and
J(K)K are infinitely generated, or
(iv) K is a prime right SI-ring with infinitely generated right socle.
For a partial converse, we also give examples of rings with no p-middle class of
types (i), (ii) and (iii).
(Joint works with Sergio R. Lopez-Permouth and Nil Orhan-Ertas, as well as Hai
Q. Dinh and Dinh van Huynh.)
OHIO UNIVERSITY
ATHENS, OH
ch327505 at ohio dot edu
pt
I will start with a brief review of pre-2000 results on the
Finitistic Dimension Conjectures (which date back to 1960), and then
discuss some recent progress. In particular, I will address jumps in the
functions
![]() for
for ![]() a natural number or
a natural number or
![]() , where
, where ![]() is a finite dimensional algebra and
is a finite dimensional algebra and
![]() is the supremum of the finite projective dimensions attained on
is the supremum of the finite projective dimensions attained on
![]() -generated left
-generated left ![]() -modules.
-modules.
UNIVERSITY OF CALIFORNIA
SANTA BARBARA, CA
birge at math dot ucsb dot edu
We prove that every infinite nilpotent associative or Lie ring admits a non-discrete locally totally bounded Hausdorff ring topology. An example of a nilpotent ring which does not admit a non-discrete bounded ring topology is given. (This is a joint work with Mihail Ursul.)
QATAR UNIVERSITY
DOHA, QATAR
martinjuras at gmail dot com
An element ![]() of a ring
of a ring ![]() is called clean if
is called clean if ![]() for some idempotent
for some idempotent ![]() and some unit
and some unit ![]() in
in ![]() . We obtain idempotents in polynomial rings and
related ring extensions and use this information to give clean elements in
polynomial rings and other related ring extensions. Among other things it is
shown that
. We obtain idempotents in polynomial rings and
related ring extensions and use this information to give clean elements in
polynomial rings and other related ring extensions. Among other things it is
shown that ![]() is abelian if and only if there exists a positive integer
is abelian if and only if there exists a positive integer ![]() such that
such that ![]() does not contain idempotents which are polynomials of
degree
does not contain idempotents which are polynomials of
degree ![]() . Idempotents of a polynomial ring which are conjugate to
idempotents in the base ring are also studied. It is shown that if
. Idempotents of a polynomial ring which are conjugate to
idempotents in the base ring are also studied. It is shown that if ![]() is
either an abelian ring or a 2-primal ring such that
is
either an abelian ring or a 2-primal ring such that ![]() is an
is an ![]() -ring
then every idempotent
-ring
then every idempotent
![]() is conjugated to a diagonal matrix
of the form
is conjugated to a diagonal matrix
of the form
![]() , where
, where ![]() 's denote
idempotents in
's denote
idempotents in ![]() . (This is a joint work with André Leroy and Jerzy
Matczuk.)
. (This is a joint work with André Leroy and Jerzy
Matczuk.)
OHIO UNIVERSITY - ZANESVILLE
ZANESVILLE, OHIO
kanwar at ohio dot edu
Let
![]() be an algebraic number field with
be an algebraic number field with ![]() in the
ring
in the
ring ![]() of algebraic integers of
of algebraic integers of ![]() and
and ![]() be the minimal polynomial of
be the minimal polynomial of
![]() over the field
over the field
![]() of rational numbers. Dedekind proved that
if a rational prime
of rational numbers. Dedekind proved that
if a rational prime ![]() does not divide
does not divide
![]() , then the
determination of the prime ideal decomposition in
, then the
determination of the prime ideal decomposition in ![]() of
of ![]() is related to the
decomposition of the polynomial
is related to the
decomposition of the polynomial
![]() obtained by replacing each
coefficient of
obtained by replacing each
coefficient of ![]() by its residue modulo
by its residue modulo ![]() . Dedekind also gave a simple
criterion known as Dedekind Criterion to verify when
. Dedekind also gave a simple
criterion known as Dedekind Criterion to verify when ![]() does not divide
does not divide
![]() In 2005 we extended Dedekind Criterion to relative
extensions of algebraic number fields. An analogue of Dedekind Criterion for
finite extensions of valued fields of arbitrary rank has also been formulated
and proved. Our method of proof has led to a set of necessary and sufficient
conditions which ensure when the integral closure
In 2005 we extended Dedekind Criterion to relative
extensions of algebraic number fields. An analogue of Dedekind Criterion for
finite extensions of valued fields of arbitrary rank has also been formulated
and proved. Our method of proof has led to a set of necessary and sufficient
conditions which ensure when the integral closure ![]() of a valuation ring
of a valuation ring ![]() having
quotient field
having
quotient field ![]() in a finite extension
in a finite extension ![]() of
of ![]() is a simple ring extension
of
is a simple ring extension
of ![]() , i.e.,
, i.e.,
![]() for some
for some ![]() . As a corollary, the classical
Theorem of Dedekind characterizing those rational primes
. As a corollary, the classical
Theorem of Dedekind characterizing those rational primes ![]() which divide the
index of an algebraic number field follows.
which divide the
index of an algebraic number field follows.
INDIAN INSTITUTE OF SCIENCE EDUCATION AND RESEARCH (IISER,
MOHALI)
S. A. S. NAGAR MOHALI, PUNJAB, INDIA
skhanduja at iisermohali dot ac dot in
An element ![]() of a ring
of a ring ![]() is said to have idempotent stable range one if for
any
is said to have idempotent stable range one if for
any ![]() in
in ![]() ,
,
![]() implies that
implies that
![]() is a unit for some idempotent
is a unit for some idempotent ![]() in
in ![]() . Clearly, an element having idempotent
stable range one is clean. We prove that in
a ring with stable range one, every
regular element has idempotent stable range one. In particular, it follows that
in a unit-regular ring every element has idempotent stable range one.
. Clearly, an element having idempotent
stable range one is clean. We prove that in
a ring with stable range one, every
regular element has idempotent stable range one. In particular, it follows that
in a unit-regular ring every element has idempotent stable range one.
This is a joint work with Zhou Wang, Jianlong Chen and Tsit-Yuen Lam.
DEPARTMENT OF MATHEMATICS, PANJAB UNIVERSITY
CHANDIGARH, INDIA
dkhurana at pu dot ac dot in
A ring, whose additive group is isomorphic to an Abelian group ![]() is called a
ring on
is called a
ring on ![]() .
An absolute ideal of an Abelian group
.
An absolute ideal of an Abelian group ![]() is a subgroup of
is a subgroup of ![]() , which is an
ideal in every ring on
, which is an
ideal in every ring on ![]() .
An Abelian group is called
.
An Abelian group is called ![]() -group if it admits a ring structure, in which
every ideal is absolute.
The problem of
-group if it admits a ring structure, in which
every ideal is absolute.
The problem of ![]() -group description was formulated in [1, problem 93].
-group description was formulated in [1, problem 93].
In this work, a description of reduced algebraically compact abelian
![]() -groups will be given.
All groups, considered in this work, are Abelian
and throughout this work "group" will mean "Abelian group".
-groups will be given.
All groups, considered in this work, are Abelian
and throughout this work "group" will mean "Abelian group".
A reduced algebraically compact group ![]() can be uniquely represented as
can be uniquely represented as
![]() ,
where
,
where ![]() is a regular direct sum
is a regular direct sum
![]() of cyclic
of cyclic ![]() -adic modules.
Moreover,
-adic modules.
Moreover,
![]() ,
where
,
where ![]() is a reduced torsion-free
is a reduced torsion-free ![]() -adic algebraically compact group,
and
-adic algebraically compact group,
and ![]() is an adjusted
is an adjusted ![]() -adic algebraically compact group [2].
-adic algebraically compact group [2].
Theorem 1.
Let ![]() be a reduced
be a reduced ![]() -adic algebraically compact group, whose torsion
subgroup is unbounded.
Let
-adic algebraically compact group, whose torsion
subgroup is unbounded.
Let
![]() ,
where
,
where
![]() is a reduced
torsion-free
is a reduced
torsion-free ![]() -adic algebraically compact group,
and
-adic algebraically compact group,
and
![]() is an adjusted
is an adjusted
![]() -adic algebraically compact group.
Let
-adic algebraically compact group.
Let
![]() ,
,
![]() . Then
. Then
1) if ![]() then
then ![]() is a
is a ![]() -group if and only if there exists a whole
number
-group if and only if there exists a whole
number ![]() such that
such that
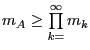 .
.
2) If ![]() , then
, then ![]() is an
is an ![]() -group if and only if
-group if and only if
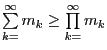 for all
for all
![]() .
.
Theorem 2.
Let ![]() be a reduced algebraically compact group,
be a reduced algebraically compact group,
![]() ,
where
,
where ![]() is a reduced
is a reduced ![]() -adic algebraically compact group, whose torsion
subgroup is unbounded.
Then
-adic algebraically compact group, whose torsion
subgroup is unbounded.
Then ![]() is a
is a ![]() -group if and only if
-group if and only if ![]() is a
is a ![]() -group for every
-group for every ![]() .
.
[1] L.Fuchs, Infinite Abelian groups // Academic Press New York and London, 1973.
[2] Kompantseva E.I. Torsion-free rings // Journal of Mathematical Sciences (New York), 2010, 171:2, 213-247.
MOSCOW STATE PEDAGOGICAL UNIVERSITY
MOSCOW, RUSSIA
kompantseva at yandex dot ru
Mason introduced the reflexive property for ideals, and then this concept was generalized by Kim and Baik, defining idempotent reflexive right ideals and rings. In this paper, we characterize aspects of the reflexive and one-sided idempotent reflexive properties, showing that the concept of idempotent reflexive ring is not left-right symmetric. It is proved that a (right idempotent) reflexive ring which is not semiprime (resp., reflexive), can always be constructed from any semiprime (resp., reflexive) ring. It is also proved that the reflexive condition is Morita invariant and that the right quotient ring of a reflexive ring is reflexive. It is shown that both the polynomial ring and the power series ring over a reflexive ring are idempotent reflexive. We obtain additionally that the semiprimeness, reflexive property and one-sided idempotent reflexive property of a ring coincide for right principally quasi-Baer rings.
DAEJIN UNIVERSITY
POCHEON,
tkkwak at daejin dot ac dot kr
An element of the form
![]() in a ring
in a ring ![]() is called an (additive) commutator, and an element of the form
is called an (additive) commutator, and an element of the form
![]() in
in ![]() is called a generalized commutator.
In this talk, we present some recent results (and problems)
on commutators and generalized commutators in a matrix ring
is called a generalized commutator.
In this talk, we present some recent results (and problems)
on commutators and generalized commutators in a matrix ring
![]() over a (not necessarily commutative) base
ring
over a (not necessarily commutative) base
ring ![]() . This is joint work with D. Khurana and V. Kodiyalam.
. This is joint work with D. Khurana and V. Kodiyalam.
UNIVERSITY OF CALIFORNIA, BERKELEY
BERKELEY, CALIFORNIA
lam at math dot berkeley dot edu
The study of the class of von Neumann regular rings has been a topic of wide
interest. In 1958 Fuchs raised the question of characterizing abelian groups
whose endomorphism rings are von Neumann regular. This was answered for the case
of groups by Rangaswamy in 1967 but independently in 1960 for the case of
modules by Azumaya. In particular, it was shown that for a module ![]() ,
End
,
End![]() is a von Neumann regular ring iff
is a von Neumann regular ring iff
![]() and
and
![]() are direct summands of
are direct summands of ![]() for every
for every
![]() End
End![]() .
.
In this work we study modules ![]() which satisfy these two conditions namely, for
all
which satisfy these two conditions namely, for
all
![]() End
End![]() ,
,
![]() is a direct summand of
is a direct summand of ![]() and
and
![]() is a direct summand of
is a direct summand of ![]() . (In fact from our recent works, a module
satisfying only the first condition is called Rickart and a module satisfying
only the second one is called dual Rickart). In view of Azumaya and Rangaswamy
results, we call a module
. (In fact from our recent works, a module
satisfying only the first condition is called Rickart and a module satisfying
only the second one is called dual Rickart). In view of Azumaya and Rangaswamy
results, we call a module ![]() satisfying the two conditions endoregular.
We will present some new results on endoregular modules and other related
notions in this talk. In particular, we will provide characterizations of
modules whose endomorphism rings are: strongly regular, unit regular, division
rings, simple artinian rings, and semisimple artinian rings, among other
classes.
Examples which delineate the concepts and results will be shown.
satisfying the two conditions endoregular.
We will present some new results on endoregular modules and other related
notions in this talk. In particular, we will provide characterizations of
modules whose endomorphism rings are: strongly regular, unit regular, division
rings, simple artinian rings, and semisimple artinian rings, among other
classes.
Examples which delineate the concepts and results will be shown.
(This is a joint work with S. Tariq Rizvi and Cosmin Roman.)
THE OHIO STATE UNIVERSITY
COLUMBUS, OH
lgy999 at math dot osu dot edu
In this talk the idea of an intrinsic extension of a ring, first
proposed by Faith and Utumi, is generalized and studied in its own right. For
these types of ring extensions, it is shown that, with relatively mild
conditions on the base ring, ![]() , a complete set of primitive idempotents (a
complete set of left triangulating idempotents, a complete set of centrally
primitive idempotents) can be constructed for an intrinsic extension,
, a complete set of primitive idempotents (a
complete set of left triangulating idempotents, a complete set of centrally
primitive idempotents) can be constructed for an intrinsic extension, ![]() , from
a corresponding set in the base ring
, from
a corresponding set in the base ring ![]() . Examples and applications are given
for rings that occur in Functional Analysis. Furthermore, it is shown that our
main results provide a new method for attempting to investigate the well-known
Zero Divisor Problem in Group Ring Theory and possibly extend partial solutions
to the problem.
. Examples and applications are given
for rings that occur in Functional Analysis. Furthermore, it is shown that our
main results provide a new method for attempting to investigate the well-known
Zero Divisor Problem in Group Ring Theory and possibly extend partial solutions
to the problem.
UNIVERSITY OF LOUISIANA LAFAYETTE
LAFAYETTE, LOUISIANA
jake.lennon at gmail dot com
We will survey results on Ore polynomial rings obtained essentially in the 90's with T.Y.Lam. We will also present some more recent results on this topic. The focus will be on factorizations problems of skew polynomials mainly with coefficients in division rings. The Wedderburn polynomials, their different characterizations and properties their relations with Vandermonde and Wronskian matrices will be at the center of the talk. We will also consider the more general completely reducible polynomials. Using pseudo-linear transformation, we will indicate how some of the results can be naturally interpreted and generalized to the case when the base ring is not a division ring. Applications to some topics such as noncommutative symmetric functions and coding theory will be mentioned.
UNIVERSITÉ D'ARTOIS
LENS, PAS DE CALAIS, FRANCE
andreleroy55 at gmail dot com
Let ![]() be a commutative ring with
be a commutative ring with ![]() ,
, ![]() be a nontrivial finite group
and let
be a nontrivial finite group
and let ![]() be the set of zero-divisors of
be the set of zero-divisors of ![]() . The zero-divisor graph of
. The zero-divisor graph of
![]() is defined as the graph
is defined as the graph
![]() with the vertex set
with the vertex set
![]() and two distinct
vertices
and two distinct
vertices ![]() and
and ![]() are adjacent if and only if
are adjacent if and only if ![]() . In this talk, we
investigate
the interplay between the ring-theoretic properties of group ring
. In this talk, we
investigate
the interplay between the ring-theoretic properties of group ring ![]() and the
graph-theoretic properties of
and the
graph-theoretic properties of
![]() . We first characterize finite abelian
group algebras
. We first characterize finite abelian
group algebras ![]() with
with
![]() as well as Artinian
commutative group rings
as well as Artinian
commutative group rings ![]() with
with
![]() . We also investigate the
isomorphic problem for zero-divisor graphs of group rings. It is shown that two
finite semisimple group rings are isomorphic if and only if their zero-divisor
graphs are isomorphic. It is also shown that rank and cardinality of a finite
abelian p-group is completely determined by the zero-divisor graph of its
modular group ring, extending a result of Akbari et al (J. Algebra 2004).
Finally, we show that a finite noncommutative reversible group ring is
completely determined by its zero-divisor graph.
. We also investigate the
isomorphic problem for zero-divisor graphs of group rings. It is shown that two
finite semisimple group rings are isomorphic if and only if their zero-divisor
graphs are isomorphic. It is also shown that rank and cardinality of a finite
abelian p-group is completely determined by the zero-divisor graph of its
modular group ring, extending a result of Akbari et al (J. Algebra 2004).
Finally, we show that a finite noncommutative reversible group ring is
completely determined by its zero-divisor graph.
Joint work with Farid Aliniaeifard.
BROCK UNIVERSITY
ST. CATHARINES, ONTARIO, CANADA
yli at brocku dot ca
Let ![]() be a ring. A left
be a ring. A left ![]() -module
-module ![]() is called a c.p. module if every cyclic
submodule of
is called a c.p. module if every cyclic
submodule of ![]() is projective. This notion is a generalization of left p.p.
rings in the module theoretic setting. In this talk, some characterizations and
properties of c.p. modules are discussed. As applications, the connections among
Baer rings, p.p. rings and von Neumann regular rings are studied. For example,
it is proved that the class of c.p. left
is projective. This notion is a generalization of left p.p.
rings in the module theoretic setting. In this talk, some characterizations and
properties of c.p. modules are discussed. As applications, the connections among
Baer rings, p.p. rings and von Neumann regular rings are studied. For example,
it is proved that the class of c.p. left ![]() -modules is closed under direct
sums. We also show that
-modules is closed under direct
sums. We also show that ![]() is Baer if and only if
is Baer if and only if ![]() is p.p. and the class of
c.p. left
is p.p. and the class of
c.p. left ![]() -modules is closed under direct products. Moreover, von Neumann
regular rings are characterized in terms of c.p. modules (joint with Professor
Jianlong Chen).
-modules is closed under direct products. Moreover, von Neumann
regular rings are characterized in terms of c.p. modules (joint with Professor
Jianlong Chen).
SOUTHEAST UNIVERSITY
NANJING, CHINA
ahlql123 at 163 dot com
In this talk, we develop some relative homological algebra in the category of functors from finitely presented modules to abelian groups. More specifically, we introduce the concepts of F-injective, F-projective and F-flat functors. These functors are discovered when we study covers and envelopes of functors. The relationships among these functors are investigated and some applications are given.
INSTITUTE OF MATHEMATICS, NANJING INSTITUTE OF TECHNOLOGY
NANJING, CHINA
maolx2 at hotmail dot com
Similar to the idea of relative projectivity, we introduce the notion of
relative subprojectivity, which is an alternative way to measure the
projectivity of a module. Given modules ![]() and
and ![]() ,
, ![]() is said to be
is said to be
![]() -subprojective if for every epimorphism
-subprojective if for every epimorphism
![]() and homomorphism
and homomorphism
![]() , then there exists a homomorphism
, then there exists a homomorphism
![]() such
that
such
that ![]() . For a module
. For a module ![]() , the subprojectivity domain of
, the subprojectivity domain of ![]() is
defined to be the collection of all modules
is
defined to be the collection of all modules ![]() such that
such that ![]() is
is
![]() -subprojective. A module is projective if and only if its subprojectivity
domain consists of all modules. Opposite to this idea, a module
-subprojective. A module is projective if and only if its subprojectivity
domain consists of all modules. Opposite to this idea, a module ![]() is said to
be
is said to
be ![]() -indigent if its subprojectivity domain is as small as conceivably
possible, that is, consisting of exactly the projective modules. Properties of
subprojectivity domains and
-indigent if its subprojectivity domain is as small as conceivably
possible, that is, consisting of exactly the projective modules. Properties of
subprojectivity domains and ![]() -indigent modules are studied. In particular,
the existence of a
-indigent modules are studied. In particular,
the existence of a ![]() -indigent module is attained for artinian serial ring.
-indigent module is attained for artinian serial ring.
This is joint work with Holston, Lopez-Permouth and Simental.
OHIO UNIVERSITY
ATHENS, OHIO
jm424809 at ohio dot edu
An associative ring ![]() is said to be a commutator ring if
is said to be a commutator ring if ![]() ,
where
,
where ![]() is the subgroup of
is the subgroup of ![]() generated by its additive commutators.
There has been interest in such rings since at least 1956, when Kaplansky asked
whether there could be a commutator division ring. To date, few examples of
rings with this property have been produced, but it turns out that many such
examples can be built using Leavitt path algebras. Commutator Leavitt path
algebras have the additional unusual property that all their Lie ideals are
(ring-theoretic) ideals. It is also possible to completely classify the
commutator Leavitt path algebras, and in the process to describe the commutator
subspace
generated by its additive commutators.
There has been interest in such rings since at least 1956, when Kaplansky asked
whether there could be a commutator division ring. To date, few examples of
rings with this property have been produced, but it turns out that many such
examples can be built using Leavitt path algebras. Commutator Leavitt path
algebras have the additional unusual property that all their Lie ideals are
(ring-theoretic) ideals. It is also possible to completely classify the
commutator Leavitt path algebras, and in the process to describe the commutator
subspace
![]() of the Leavitt path algebra
of the Leavitt path algebra ![]() , for any field
, for any field
![]() and directed graph
and directed graph ![]() .
.
UNIVERSITY OF COLORADO, COLORADO SPRINGS
COLORADO SPRINGS, CO
zmesyan at uccs dot edu
A necessary and sufficient condition is obtained for a right pseudo semisipmle ring to be left pseudo semisimple. It is also proved that a right and left pseudo semisimple ring is an internal exchange ring and is an SSP ring.
IZMIR INSTITUTE OF TECHNOLOGY
IZMIR, TURKEY
hatcemutlu at gmail dot com
In 1995 Camillo and Yu showed that an exchange ring has stable range 1 if and only if every regular element is unit-regular. A definition of a stable module is given and the analogous theorem is proved.
UNIVERSITY OF CALGARY
CALGARY, ALBERTA
wknichol at ucalgary dot ca
The set
![]() is nil of bounded index
is nil of bounded index![]() is an ideal. This
was first proved by Amitsur, and then given another proof by Klein. Klein also
proved that
is an ideal. This
was first proved by Amitsur, and then given another proof by Klein. Klein also
proved that
![]() . We provide new intuitive proofs for these facts,
and show that these proofs generalize to skew polynomial rings more easily than
the earlier proofs.
. We provide new intuitive proofs for these facts,
and show that these proofs generalize to skew polynomial rings more easily than
the earlier proofs.
BRIGHAM YOUNG UNIVERSITY
PROVO, UT
pace at math dot byu dot edu
We study polycyclic codes over Galois rings which are generalizations of cyclic
codes.
These codes have a nice algebraic structure as they can be viewed as ideals of
a factor ring of a polynomial ring. We study the structure of the ambient ring
of polycyclic codes.
We show the existence of a certain type of a generating set for an ideal of this
ring.
This generating set turns out to be a strong Groebner basis.
We provide a method for finding such sets over a Galois ring of characteristic
![]() .
We also give a method to determine the Hamming distance of the constacyclic
codes of length
.
We also give a method to determine the Hamming distance of the constacyclic
codes of length
![]() and
and ![]() over a Galois ring of characteristic
over a Galois ring of characteristic ![]() .
.
This is a joint work with Sergio R. Lopez-Permouth, Ferruh Ozbudak and Steve Szabo.
OHIO UNIVERSITY, DEPARTMENT OF MATHEMATICS, PHD STUDENT
ATHENS, OHIO
ho379511 at ohio dot edu
In this talk, some ![]() -clean rings will be introduced and various properties of
them will be presented.
-clean rings will be introduced and various properties of
them will be presented.
Joint work with H. Chen and A. Harmanci
HACETTEPE UNIVERSITY
ANKARA, TURKEY
ozcan at hacettepe dot edu dot tr
Following Lopez-Permouth, Moore and Szabo, a ![]() -algebra
-algebra ![]() is called an
invertible algebra if it has a
is called an
invertible algebra if it has a ![]() -basis of units in A. The purpose of
this project is to determine the directed graphs
-basis of units in A. The purpose of
this project is to determine the directed graphs ![]() for which the Leavitt path
algebra
for which the Leavitt path
algebra ![]() is an invertible algebra. Among other results, we show that all
noetherian Leavitt path algebras are invertible. We also describe another
family of invertible Leavitt path algebras which includes, for all
is an invertible algebra. Among other results, we show that all
noetherian Leavitt path algebras are invertible. We also describe another
family of invertible Leavitt path algebras which includes, for all ![]() the
classical Leavitt algebra
the
classical Leavitt algebra ![]() (This is joint work with Al-Essa,
López-Permouth and Simental).
(This is joint work with Al-Essa,
López-Permouth and Simental).
OHIO UNIVERSITY
ATHENS, OH
np338697 at ohio dot edu
This inquiry is based on both the construction of generalized incidence rings due to Gene Abrams and the construction of good group gradings of incidence algebras due to Molli Jones. The speaker will provide conditions for a generalized incidence ring to be graded isomorphic to a subring of an incidence ring over a preorder. An extension of Jones’s construction to good group gradings for incidence algebras over preorders with crosscuts of length one or two will also be covered.
UNIVERSITY OF WISCONSIN, OSHKOSH
OSHKOSH, WI
pricek at uwosh dot edu
Let ![]() be an associative ring. An additive subgroup
be an associative ring. An additive subgroup ![]() of
of ![]() is said to be a
Lie ideal of
is said to be a
Lie ideal of ![]() if
if
![]() . An additive mapping
. An additive mapping
![]() is called a derivation (resp. a Jordan derivation) if
is called a derivation (resp. a Jordan derivation) if
![]() (resp.
(resp.
![]() holds for all
holds for all
![]() . A famous result due to Herstein states
that a Jordan derivation in a prime ring of characteristic not equal to
. A famous result due to Herstein states
that a Jordan derivation in a prime ring of characteristic not equal to ![]() must
be a derivation. This result was extended to 2-torsion free semiprime rings by
Cusack and subsequently, by Bresar.
must
be a derivation. This result was extended to 2-torsion free semiprime rings by
Cusack and subsequently, by Bresar.
Following Bresar [Jordan mappings of semiprime rings, J. Algebra 127 (1989),
218-228], an additive mapping
![]() is called a Jordan
triple derivation if
is called a Jordan
triple derivation if
![]() holds for all
holds for all
![]() . One can easily prove that any Jordan derivation of a
. One can easily prove that any Jordan derivation of a ![]() -torsion free ring
is a Jordan triple derivation. An additive mapping
-torsion free ring
is a Jordan triple derivation. An additive mapping
![]() is
said to be a generalized Jordan triple derivation on
is
said to be a generalized Jordan triple derivation on ![]() if there exists a
Jordan triple derivation
if there exists a
Jordan triple derivation
![]() such that
such that
![]() holds for all
holds for all ![]() .
.
It is obvious to see that every derivation is a Jordan triple derivation but the
converse need not be true in general. In 1989, Bresar proved that any Jordan
triple derivation on a ![]() -torsion free semiprime ring is a derivation. In the
present talk, my attempt will be to extend this study further and obtain some
results on Lie idesls. Also two conjuctures will be presented for open
discussion (if not settled by the time, the talk will be given).
-torsion free semiprime ring is a derivation. In the
present talk, my attempt will be to extend this study further and obtain some
results on Lie idesls. Also two conjuctures will be presented for open
discussion (if not settled by the time, the talk will be given).
DEPARTMENT OF MATHEMATICS, ALIGARH MUSLIM UNIVERSITY
ALIGARH, UTTER PRADESH, INDIA
maquadri1 at rediffmail dot com
Using commutativity of rings satisfying
![]() proved by Searcoid and
MacHale [Amer. Math. Monthly 93 (1986)], Ligh and Luh [Amer. Math. Monthly 96
(1989)] gave a direct sum decomposition for rings with the
proved by Searcoid and
MacHale [Amer. Math. Monthly 93 (1986)], Ligh and Luh [Amer. Math. Monthly 96
(1989)] gave a direct sum decomposition for rings with the
mentioned
condition. Further, Bell and Ligh [Math. J. Okayama Univ.31 (1989)] sharpened
the result and obtained a decomposition theorem for rings with the property
![]() where
where
![]() , the ring of polynomials in
two noncommuting indeterminates over the ring
, the ring of polynomials in
two noncommuting indeterminates over the ring
![]() of integers. In the
present paper, we continue the study and investigate structure of certain rings
and near rings satisfying the following condition:
of integers. In the
present paper, we continue the study and investigate structure of certain rings
and near rings satisfying the following condition:
![]() with
with ![]() ,
an admissible polynomial in
,
an admissible polynomial in
![]() . This condition is naturally
more general than the above mentioned conditions. Moreover, we deduce the
commutativity of such rings.
. This condition is naturally
more general than the above mentioned conditions. Moreover, we deduce the
commutativity of such rings.
Theorem 1. Let ![]() be a ring such that for each
be a ring such that for each ![]() there
exists an admissible polynomial
there
exists an admissible polynomial
![]() for which
for which
![]() . Then
. Then ![]() is a direct sum of a
is a direct sum of a ![]() -ring and a zero ring.
-ring and a zero ring.
Theorem 2. Let ![]() be a d-g near ring such that for each
be a d-g near ring such that for each ![]() there exists an admissible polynomial
there exists an admissible polynomial
![]() for which
for which
![]() . Then
. Then ![]() is periodic and commutative. Moreover,
is periodic and commutative. Moreover,
![]() , where P,
the set of potent elements of
, where P,
the set of potent elements of ![]() is a subring and N, the set of nilpotent
elements of
is a subring and N, the set of nilpotent
elements of ![]() is a subnear ring with trivial multiplication.
is a subnear ring with trivial multiplication.
N. R. E. C. COLLEGE
BULANDSHAHAR, UTTER PRADESH, INDIA
rekharani at rediffmail dot com
I will present the following obstruction result for functors extending the
Zariski spectrum to noncommutative rings: every contravariant functor from the
category of rings to the category of sets whose restriction to the full
subcategory of commutative rings is isomorphic to
![]() must assign
the empty set to
must assign
the empty set to
![]() for
for ![]() . The proof relies on
the Kochen-Specker ``no-hidden-variables'' theorem of quantum mechanics. I will
also mention a recent generalization of the result due to van den Berg and
Heunen.
. The proof relies on
the Kochen-Specker ``no-hidden-variables'' theorem of quantum mechanics. I will
also mention a recent generalization of the result due to van den Berg and
Heunen.
BOWDOIN COLLEGE
BRUNSWICK, ME
reyes at bowdoin dot edu
In his famous book on the icosahedron, Felix Klein considered the identification
of a point on the unit sphere u, with the linear form x - vy, where v is the
image of u under the Riemann map. If you start with the vertices of a nice
polytope inscribed in the sphere, and
take quadratic forms corresponding to products of linear forms associated with
antipodal pairs of vertices, you get interesting sets of quadratic forms. For
example, the octahedron corresponds to
![]() (the
Pythagorean parameterization), the cube to four quadratic forms whose 5-th
powers are dependent and the icosahedron to six quadratic forms whose 14-th
powers are dependent. We'll give more examples and try to explain this
phenomenon.
(the
Pythagorean parameterization), the cube to four quadratic forms whose 5-th
powers are dependent and the icosahedron to six quadratic forms whose 14-th
powers are dependent. We'll give more examples and try to explain this
phenomenon.
UNIVERSITY OF ILLINOIS
URBANA, IL
reznick at math dot uiuc dot edu
A left Rickart (respectively, left Baer) ring is one in which the left annihilator of any element (respectively, arbitrary nonempty subset) is generated by an idempotent. Right-sided notions are defined similarly. It is well-known that the notion of a Baer ring is always left-right symmetric while the notion of a Rickart ring is not left-right symmetric.
We recently extended the right Rickart property of rings to a module-theoretic
setting, and called it a Rickart module. On the other hand, the study of left
Rickart rings in this general setting remains open. In this talk we present a
module theoretic analogue of a left Rickart ring and call it an
Endo-Rickart module. A ![]() -module
-module ![]() is called
Endo-Rickart if the left annihilator in
is called
Endo-Rickart if the left annihilator in ![]() of an element of
of an element of ![]() is a left direct summand in
is a left direct summand in ![]() .
.
In this talk we present results and properties of Endo-Rickart modules and ancillary notions. Examples and applications will also be provided.
(This is a joint work with G. Lee and S. Tariq Rizvi.)
THE OHIO STATE UNIVERSITY, LIMA
LIMA, OH
cosmin at math dot osu dot edu
The Mittag-Leffler property constitutes a useful generalization of (pure) projectivity. I will discuss some new results about it.
GRADUATE CENTER OF CUNY
NEW YORK, NY
philipp.rothmaler at bcc dot cuny dot edu
We introduce a general decomposition for a large class of modules over rings
with unity. In particular,
it is shown that for a given set of pairwise comaximal ideals
![]() in the ring, if
in the ring, if ![]() is
a right
is
a right ![]() -module such that
-module such that
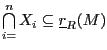 , then
, then ![]() is a direct
sum of the
is a direct
sum of the
![]() , where
, where
![]() . Several well-
known results from commutative ring theory and the theory of semisimple Artinian
rings are presented
as examples of our main theorem. Also some torsion theoretical results related
to our
decompositions will be shown. This talk is based on joint work with Gary F.
Birkenmeier.
. Several well-
known results from commutative ring theory and the theory of semisimple Artinian
rings are presented
as examples of our main theorem. Also some torsion theoretical results related
to our
decompositions will be shown. This talk is based on joint work with Gary F.
Birkenmeier.
UNIVERSITY OF LOUISIANA AT LAFAYETTE
LAFAYETTE, LOUISIANA
cxr2665 at louisiana dot edu
We study geometric properties of varieties associated with invariant subspaces of nilpotent operators. There are reductive algebraic groups acting on these varieties. We give dimensions of orbits of these actions. Moreover, a combinatorial characterization of the partial order given by degenerations is described. This is a report about a joint project with Justyna Kosakowska from Torun in Poland.
FLORIDA ATLANTIC UNIVERSITY
BOCA RATON,
markus at math dot fau dot edu
We will start this talk by showing the current picture concerning the classification of Leavitt path algebras. We will see that primitive idempotents play an essential role, in particular, the primitive ones. We will introduce the notion of truly primitive idempotent, closely related to Condition (L) and will show its implication in such a classification.
UNIVERSIDAD DE MALAGA
MALAGA, SPAIN
msilesm at uma dot es
Given a ring ![]() , we define its right
, we define its right ![]() -profile (resp. right
-profile (resp. right ![]() -profile) as
the collection of injectivity domains (resp. projectivity domains) of its right
modules. We show that the
-profile) as
the collection of injectivity domains (resp. projectivity domains) of its right
modules. We show that the ![]() -profile of a ring has a natural lattice structure,
and we study its properties, while the
-profile of a ring has a natural lattice structure,
and we study its properties, while the ![]() -profile has a semilattice structure.
We also characterize those rings for which the projectivity and injectivity
domain of every module coincide. The study of the profile(s) of a ring has
various connections to torsion theory and with the theory of poor modules and
rings with no middle class, recently introduced by Er, López-Permouth,
Sökmez, Holston and Orhan-Ertas. (Joint work with Sergio R.
López-Permouth)
-profile has a semilattice structure.
We also characterize those rings for which the projectivity and injectivity
domain of every module coincide. The study of the profile(s) of a ring has
various connections to torsion theory and with the theory of poor modules and
rings with no middle class, recently introduced by Er, López-Permouth,
Sökmez, Holston and Orhan-Ertas. (Joint work with Sergio R.
López-Permouth)
OHIO UNIVERSITY
ATHENS, OHIO
jesr_ at hotmail dot com
We call a module ![]() to be a dual automorphism-invariant module if whenever
to be a dual automorphism-invariant module if whenever
![]() and
and ![]() are small submodules of
are small submodules of ![]() , then any epimorphism
, then any epimorphism
![]() with small kernel lifts to an endomorphism
with small kernel lifts to an endomorphism
![]() of
of ![]() . In this talk we will give various examples of dual
automorphism-invariant modules and discuss their properties. (This is a joint
work with Surjeet Singh)
. In this talk we will give various examples of dual
automorphism-invariant modules and discuss their properties. (This is a joint
work with Surjeet Singh)
ST. LOUIS UNIVERSITY
SAINT LOUIS, MO
asrivas3 at slu dot edu
An element of a ring ![]() is called clean if it can be written as a sum
of an idempotent and a unit in
is called clean if it can be written as a sum
of an idempotent and a unit in ![]() . A ring is called clean if its every
element is clean. Clean rings arise as a special example of exchange rings. An
example due to Bergman shows that an exchange ring does not need to be clean.
. A ring is called clean if its every
element is clean. Clean rings arise as a special example of exchange rings. An
example due to Bergman shows that an exchange ring does not need to be clean.
It is known that the clean property is closed under matrix extensions, meaning
that if ![]() is clean, then
is clean, then ![]() is clean. The converse of this proposition
is still an open problem. More generally, it is not known whether
is clean. The converse of this proposition
is still an open problem. More generally, it is not known whether ![]() being
clean implies that
being
clean implies that ![]() is clean for a full idempotent
is clean for a full idempotent ![]() .
.
In the talk, we classify all rings ![]() with the property that the matrices
with the property that the matrices
![]() are clean in
are clean in
![]() for every
for every ![]() . We show that the Bergman's ring satisfies this
property, and using this observation, we give an example of a clean ring
. We show that the Bergman's ring satisfies this
property, and using this observation, we give an example of a clean ring ![]() and
an idempotent
and
an idempotent ![]() such that the corner ring
such that the corner ring ![]() is not clean.
is not clean.
INSTITUTE OF MATHEMATICS, PHYSICS AND MECHANICS
LJUBLJANA, SLOVENIA
janez.ster at fmf dot uni-lj dot si
We describe surjective additive maps
![]() which preserve zero
products (i.e.
which preserve zero
products (i.e. ![]() implies
implies
![]() ), where
), where ![]() is a ring with
a nontrivial idempotent and
is a ring with
a nontrivial idempotent and ![]() is a prime ring. We also characterize surjective
additive maps
is a prime ring. We also characterize surjective
additive maps
![]() such that
such that
![]() if and
only if
if and
only if ![]() , where
, where ![]() is a unital prime ring with involution that
contains a nontrivial idempotent and
is a unital prime ring with involution that
contains a nontrivial idempotent and ![]() is a prime ring with involution.
is a prime ring with involution.
UNIVERSITY OF LJUBLJANA
LJUBLJANA, SLOVENIA
nik.stopar at fmf dot uni-lj dot si
In this note we prove that any ring ![]() is right cosemihereditary if and only if
every finitely cogenerated injective right
is right cosemihereditary if and only if
every finitely cogenerated injective right ![]() -module is
-module is ![]() -Rickart. We also
prove that if
-Rickart. We also
prove that if
![]() with
with ![]() semisimple, then
semisimple, then ![]() is dual Baer if and only if
is dual Baer if and only if ![]() is dual Baer
and every simple non-direct summand of
is dual Baer
and every simple non-direct summand of ![]() does not embed in
does not embed in ![]() .
.
Joint work with Derya Keskin Tütüncü and Patrick F. Smith.
IZMIR INSTITUTE OF TECHNOLOGY
IZMIR, TURKEY
eylemtoksoy at iyte dot edu dot tr
We present some recent results from [1]-[6] on flat Mittag-Leffler
(![]() -projective) modules, and their consequences for generalized vector
bundles.
-projective) modules, and their consequences for generalized vector
bundles.
References.
S. BAZZONI, J. ŠŠ
G. BRAUN, J. TRLIFAJ,
Strong submodules of almost projective modules,
Pacific J. Math.
254 (2011), 73-87.
S. ESTRADA, P. GUIL ASENSIO, J. TRLIFAJ,
Descent of restricted flat Mittag-Leffler modules
and generalized vector bundles, arXiv:1110.5364.
Infinite-dimensional vector bundles in algebraic geometry: an
introduction, in 'The Unity of Mathematics', Birkhäuser, Boston
2006, 263-304.
D.HERBERA, J.TRLIFAJ,
Almost free modules and Mittag-Leffler conditions,
Advances in Math. 229(2012), 3436-3467.
J.ŠAROCH, J.TRLIFAJ,
Kaplansky classes, finite character, and
UNIVERZITA KARLOVA
We introduce principally
ANKARA UNIVERSITY
The talk presents three directions of research motivated by T. Y. Lam's work.
The inspiration comes from: (1) Lam's view of classical rings of quotients as
``the Good, the Bad and the Ugly'' from ``Lectures on Rings and Modules''; (2)
Lam's question ``Which von Neumann algebras are clean as rings?'' from the
Athens, OH conference in 2005; (3) Lam's treatment of uniform dimension in
``Lectures on Rings and Modules''.
UNIVERSITY OF THE SCIENCES
A right
This is a joint work with Professor Ismail Amin of Cairo University and our
Ph.D. student Mr. Yasser Ibrahim of Cairo University.
THE OHIO STATE UNIVERSITY AT LIMA
In general, the injective cover (projective envelope) of a simple module can be
zero. A ring
DEPARTMENT OF MATHEMATICS, SOUTHEAST UNIVERSITY
Motivated by recent work on uniquely clean rings, we introduce and discuss the
clean index of a ring. Rings of small clean index are characterized. (Joint work
with Tsiu-Kwen Lee)
MEMORIAL UNIVERSITY OF NEWFOUNDLAND
A ring
WARSAW UNIVERSITY OF TECHNOLOGY
![]() -projectivity,
Forum Math. 24(2012).
-projectivity,
Forum Math. 24(2012).
PRAGUE, CZECH REPUBLIC
trlifaj at karlin dot mff dot cuni dot cz
![]() -supplemented modules
-supplemented modules![]() -supplemented
modules as a generalization of
-supplemented
modules as a generalization of ![]() -supplemented modules and principally
lifting modules. This class of modules is a strengthening of principally
supplemented modules. We show that the class of principally
-supplemented modules and principally
lifting modules. This class of modules is a strengthening of principally
supplemented modules. We show that the class of principally
![]() -supplemented modules lies strictly between classes of
-supplemented modules lies strictly between classes of
![]() -supplemented modules and principally supplemented modules. We prove
that some results of
-supplemented modules and principally supplemented modules. We prove
that some results of ![]() -supplemented modules and principally lifting
modules can be extended to principally
-supplemented modules and principally lifting
modules can be extended to principally ![]() -supplemented modules for this
general settings. We obtain some characterizations of principally
semiperfect rings and von Neumann regular rings by using principally
-supplemented modules for this
general settings. We obtain some characterizations of principally
semiperfect rings and von Neumann regular rings by using principally
![]() -supplemented modules.
-supplemented modules.
ANKARA, TURKEY
burcuungor at gmail dot com
PHILADELPHIA, PA
l.vas at usciences dot edu
![]() -module
-module ![]() is called a
is called a ![]() -module, if
-module, if ![]() and
and ![]() are direct summands of
are direct summands of ![]() , with
, with
![]() then
then
![]() is a direct summand of
is a direct summand of ![]() . Besides projective,
quasi-projective and direct-projective modules, examples of
. Besides projective,
quasi-projective and direct-projective modules, examples of ![]() -modules
include discrete and quasi-discrete modules, uniform and indecomposable
modules, semisimple modules, Baer modules and
-modules
include discrete and quasi-discrete modules, uniform and indecomposable
modules, semisimple modules, Baer modules and ![]() -modules. In this talk we
obtain several interesting and new characterizations of several well-known
classes of rings in terms of
-modules. In this talk we
obtain several interesting and new characterizations of several well-known
classes of rings in terms of ![]() -modules. For example, we will show that a
ring
-modules. For example, we will show that a
ring ![]() is right perfect if and only if every flat right
is right perfect if and only if every flat right ![]() -module is a
-module is a ![]() -module, and
-module, and ![]() is right (semi)hereditary if and only if every principal
right ideal of
is right (semi)hereditary if and only if every principal
right ideal of
![]() is a
is a ![]() -module, for any (finitely generated)
free right
-module, for any (finitely generated)
free right ![]() -module
-module ![]() Following H. Bass, an
Following H. Bass, an ![]() -homomorphism
-homomorphism
![]() is called a
is called a ![]() -cover of the right
-cover of the right ![]() -module
-module ![]() , if
, if ![]() is a
is a ![]() -module,
-module, ![]() is an epimorphism, and
is an epimorphism, and ![]() is
small in
is
small in ![]() We will show that a ring
We will show that a ring ![]() is right (semi)perfect if and
only if every (finitely-generated) right
is right (semi)perfect if and
only if every (finitely-generated) right ![]() -module has a
-module has a ![]() -cover, and a
ring
-cover, and a
ring ![]() is semiregular if and only if every finitely presented right
is semiregular if and only if every finitely presented right ![]() -module has a
-module has a ![]() -cover. While projectivity is viewed more generally as a
homological condition, the strength and generality of our results stems from
the fact that the
-cover. While projectivity is viewed more generally as a
homological condition, the strength and generality of our results stems from
the fact that the ![]() -condition is a latticial condition and the proofs are
module theoretic proofs. At the end of our talk we will provide a
dualization of these results to
-condition is a latticial condition and the proofs are
module theoretic proofs. At the end of our talk we will provide a
dualization of these results to ![]() -modules.
-modules.
LIMA, OHIO
yousif.1 at osu dot edu
![]() is called a weakly left V-ring (strongly left Kasch ring) if
every simple left
is called a weakly left V-ring (strongly left Kasch ring) if
every simple left ![]() -module has a nonzero injective cover (projective
envelope). It is proved that every nonzero left
-module has a nonzero injective cover (projective
envelope). It is proved that every nonzero left ![]() -module has a nonzero
injective cover if and only if
-module has a nonzero
injective cover if and only if ![]() is a left artinian weakly left V-ring.
Dually, every nonzero left
is a left artinian weakly left V-ring.
Dually, every nonzero left ![]() -module has a nonzero projective envelope if and
only if
-module has a nonzero projective envelope if and
only if ![]() is a left perfect right coherent strongly left Kasch ring. Some
related rings and examples are concerned. (This is a joint work with X. Song)
is a left perfect right coherent strongly left Kasch ring. Some
related rings and examples are concerned. (This is a joint work with X. Song)
NANJING, CHINA
z990303 at seu dot edu dot cn
ST.JOHN'S, CANADA
zhou at mun dot ca
![]() is called right McCoy if whenever non-zero polynomials
is called right McCoy if whenever non-zero polynomials
![]() and
and
![]() in
in ![]() satisfy
satisfy
![]() , then
, then ![]() for some
for some ![]() . A ring
. A ring ![]() is Armendariz if
is Armendariz if
![]() implies
implies ![]() for all
for all ![]() and
and
![]() .
In my talk I am going to present some new results concerning above mentioned
classes of rings.
(This talk is based on joint work with Ryszard Mazurek.)
.
In my talk I am going to present some new results concerning above mentioned
classes of rings.
(This talk is based on joint work with Ryszard Mazurek.)
WARSAW, MAZOWIECKIE, POLAND
m.ziembowski at mini dot pw dot edu dot pl
Up: PROGRAM