Ring Theory Abstracts

Modules over Infinite Dimensional Algebras

LULWAH AL-ESSA, Ohio University

Let A be an infinite dimensional K- algebra, where K is a field and let B be a basis for A. In this talk we explore a property of the basis B that guarantees that $K^B$ (the direct product of copies indexed by B of the field K) can be made into an A-module in a natural way. We call bases satisfying that property "amenable" and we show that not all amenable bases yield isomorphic A-modules. Then we consider a relation (which we name congeniality) that guarantees that two different bases yield isomorphic A-module structures on $K^B$. We will look at several examples in the familiar setting of the algebra $K[x]$ of polynomials with coefficients in K. If time allows it, we will discuss some results regarding these notions in the context of Leavitt Path Algebras.

(joint work with Sergio R. López-Permouth and Najat Muthana)

ATHENS, OU
La165005 at ohio.edu

On centralizing derivations in rings with applications

SHAKIR ALI, Aligarh Muslim University, Aligarh

Let $R$ be an associative ring(algebra) with center $Z(R)$. For every associative ring $R$ can be turned into a Lie ring(algebra) by introducing a new product $[x,y] = xy - yx$, known as Lie product. So we may regard $R$ simultaneously as an associative ring(algebra) and as a Lie ring(algebra). An additive mapping $d:R \to R$ is called a derivation on $R$ if $d(xy)=d(x)y+xd(y)$ holds for all $x,y\in R$. A function $f:R \to R$ is said to be a centralizing on $R$ if $[f(x), x)] \in Z(R)$ holds for all $x \in R$. In the special case where $[f(x), x)]=0$ for all $x \in R$, $f$ is said to be commuting on $R$. The study of such mappings were initiated by E.C. Posner [ Proc. Amer. Math. Soc. 8(1957), 1093-1100]. In 1957, he proved that if a prime ring $R$ has a nonzero commuting derivation on $R$, then $R$ is commutative. An analogous result for centralizing automorphisms on prime rings was obtained by J.H. Mayne [Canad. J. Math. 19 (1976), 113-115].

In this talk, we will discuss the recent progress made on centralizing and commuting mappings in rings and algebras. Moreover, some examples and counter examples will be discussed for questions raised naturally.

ALIGARH MUSLIM UNIVERSITY, ALIGARH
ALIGARH, U.P.
shakir.ali.mm at amu.ac.in

Constacyclic codes over finite chain ring of characteristic $p$

YOUSEF ALKHAMEES, King Saud University

(Joint work with Sami Alabaid.)

We classify all constacyclic codes of finite length $p^s$ over finite chain ring R of characteristic equal to any prime number p and obtain the number of codewords in each of those cyclic codes.

References

[1] Y. Alkhamees, The determination of the group of automorphisms of a finite chain ring of characteristic P. [2] S.D. Berman, Semisimple cyclic and Abelian codes. II, Kibernetika (Kiev) 3 (1967) 21-30 (in Russian); translated as Cybernetics 3 (1967) 17-23. [3] G. Castagnoli, J.L. Massey, A.P. Schoeller, N. von Seemann, On repeated-root cyclic codes, IEEE Trans. Inform. Theory 37 (1991)337-342. [4] W.E. Clark, A coefficient ring of finite commutative chain rings, Proc. Amer. Math. Soc. [5] H.Q. Dinh, Constacyclic codes of length $P^s$ over $F_(P^m )+uF_(P^m )$. Journal of Algebra 324 (2010) 940-950. [6] H.Q.Dinh, Negacyclic codes of length $2^s$ over Galois rings, IEEE Trans. Inform. Theory 51 (2005) 4252-4262. [7] H.Q. Dinh, On the linear ordering of some classes of negacyclic and cyclic codes and thier distance distribution, Finite Fields Appl. 14 (2008) 22-40. [8] H.Q. Dinh, S.R. Lopez-permuth, Cyclic and negacyclic codes over finite chain rings, IEEE Trans. Inform. Theory 50 (2004) 1728- 1744. [9] W.C. Human, V. Pless, Fundamental of Error-Correcting codes, Cambridge University Press, Cambridge 2003. [10] F.J. MacWilliams, N.J.A Sloane, The Theory of Error-Correcting Codes 10th Impression, North-Holland, Amsterdam, 1998. [11] J.L. Massey, D.J. Castello, J. Justesen, Polynomial weights and code construction IEEE Trans. Inform. Theory 19 (1973) 101- 110. [12] V. Pless, W.C. Human, Handbook of Coding Theory, Elsevier, Amsterdam, 1998. [13] R.M. Roth, G. Seroussi, On cyclic MDS codes of length q over GR(q), IEEE Trans. Inform. Theory 32 (1986) 284- 285. [14] A. Salagean, Repeated-root cyclic and negacyclic codes over finite chain ring. Discrete Appl. Math. 154 (2006) 413-285. [15] G. Norton, A. Salagean-Mandache, On the structure of linear cyclic codes over finite chain rings, Appl. Algebra Engrg. Comm. Comput 10 (2000) 489-506. [16] P. Udaya, M.U. Siddiqi, Optimal large linear complexity frequency hopping patterns derived from polynomials residue class ring, IEEE Trans. Inform. Theory 44(1998) 1492-1503. [17] J.H. Van Lint, Repeated-root cyclic codes, IEEE Trans. Inform. Theory 37 (1991) 343- 345. [18] B.R. Writ, Finite non-commutative local rings, Ph.D. Theses, University of Oklahoma, (1972).

KING SAUD UNIVERSITY
RIYADH, SAUDI ARABIA
ykhamees at gmail.com

Difference Set Pairs : A Recursive Approach via group rings

KRISHNASAMY THIRU ARASU, Wright State University

Binary array pairs with optimal/ideal correlation values and their algebraic counterparts "difference set pairs" (DSPs) in abelian groups are studied. In addition to generalizing known 1-dimensional (sequences) examples, we provide four new recursive constructions, unifying previously obtained ones. Any further advancements in the construction of binary sequences/arrays with optimal/ideal correlation values (equivalently cyclic/abelian dfference sets) would give rise to richer classes of DSPs (and hence binary perfect array pairs). Discrete signals arising from DSPs find applications in cryptography, radar and wireless communications and CDMA systems. Our methods would employ group rings. This is a joint work with Anika Goyal and Abhishek Puri.

WRIGHT STATE UNIVERSITY
DAYTON, OH
k.arasu at wright.edu

ON GENERALIZED n-DERIVATIONS AND RELATED MAPPINGS IN NEAR-RINGS

MOHAMMAD ASHRAF, ALIGARH MUSLIM UNIVERSITY

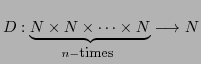Let $N$ be a zero-symmetric near-ring. A map $D:\underbrace{N \times N \times\cdots \times N }_{n-\mbox{\small times }} \longrightarrow N$ is said to be permuting if the equation $D (x_1,x_2,\cdots,x_n)= D (x_ {\pi(1)},x_{\pi(2)},\cdots,x_{\pi(n)})$ holds for all $x_1,x_2,\cdots,x_n \in N$ and for every permutation $\pi\in S_n$, where $S_n$ is the permutation group on $\{1,2,\cdots,n\}$. 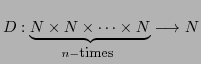A permuting $n$-additive(i.e., additive in each argument) mapping $D:\underbrace{N \times N \times\cdots \times N }_{n-\mbox{\small times }} \longrightarrow N$ is called a permuting $n$-derivation if $D(x_1 x_1^{'},x_2,\cdots,x_n) = D(x_1,x_2,\cdots,x_n) x_1^{'} + x_1 D(x_1^{'},x_2,\cdots,x_n)$ holds for all $x_1,x_1^{'},\cdots,x_n\in N$. Of course, a permuting $1$- derivation is a derivation and permuting $2$-derivation is a symmetric bi-derivation.The concepts of symmetric bi-derivation and permuting $n$-derivation have already been introduced in rings by G. Maksa, [C. R. Math. Rep. Sci. Canada,9(1987), 303-307] and Park, K.H. and Jung, Y.S., [Commun. Korean Math. Soc. 25 , (2010), 1-9] respectively. 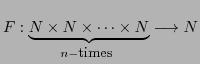Motivated by these concepts, we introduce generalized permuting $n$-derivations in near-rings as follows: A permuting $n$-additive mapping $F:\underbrace{N \times N \times\cdots \times N}_ {n-\mbox{\small times }}\longrightarrow N$ is called a right generalized permuting $n$-derivation (resp. 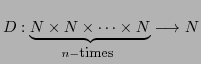a left generalized permuting $n$-derivation) if there exists a permuting $n$-derivation $D:\underbrace{N \times N \times\cdots \times N }_{n-\mbox{\small times }} \longrightarrow N$ such that $F(x_1 x_1^{'},x_2,\cdots,x_n) = F(x_1,x_2,\cdots,x_n) x_1^{'} + x_1 D(x_1^{'},x_2,\cdots,x_n)$ holds for all $x_1,x_1^{'},\cdots,x_n\in N$ (resp. $F(x_1 x_1^{'},x_2,\cdots,x_n) = D(x_1,x_2,\cdots,x_n) x_1^{'} + x_1 F(x_1^{'},x_2,\cdots,x_n)$ holds for all $x_1,x_1^{'},\cdots,x_n\in N$). If $F$ is both left as well as right generalized permuting $n$-derivation then it is called a generalized permuting $n$-derivation. Several results obtained earlier in the setting of symmetric bi-derivations, permuting tri-derivations, and permuting $n$-derivations have been generalized for permuting generalized $n$-derivations in $N$. Further, several necessary and sufficient conditions have been obtained which yield additive and multiplicative commutativity of $N$.

ALIGARH MUSLIM UNIVERSITY
ALIGARH, U.P.
mashraf80 at hotmail.com

The largest strong left quotient ring of a ring

VLADIMIR BAVULA, University of Sheffield/School of Mathematics

For an arbitrary ring R, the largest strong left quotient ring Q(R) of R and the strong left localization radical are introduced and their properties are studied in detail. A criterion is given for the ring Q(R) to be a semisimple ring. There is a canonical homomorphism from the classical left quotient ring to Q(R) which is not an isomorphism, in general.

UNIVERSITY OF SHEFFIELD/SCHOOL OF MATHEMATICS
SHEFFIELD,
v.bavula at sheffield.ac.uk

Noncommutative piecewise Noetherian rings

JOHN A BEACHY, Northern Illinois University

We extend the definition of a piecewise Noetherian ring to the noncommutative case, and investigate various properties of such rings. In particular, we show that the Gabriel correspondence between prime ideals and indecomposable injective modules holds for (noncommutative) piecewise Noetherian rings satisfying Gabriel's condition H. (Joint work with Abigail C. Bailey)

NORTHERN ILLINOIS UNIVERSITY
DEKALB, ILLINOIS
beachy at math.niu.edu

$pgs$-Extensions of Commutative Rings

PAPIYA BHATTACHARJEE, Penn State Erie

Abstract: : If $R$ and $S$ are two commutative rings with identity, and $f:R\rightarrow S$ is an injective ring homomorphism, then we can consider $R$ as a subring of $S$, and we say that $R\hookrightarrow S$ is a ring extension. An extension of rings $R\hookrightarrow S$ is a $pgs$-extension if for all $s\in S$, $sS$ nonzero implies that $sS\cap R$ is nonzero and principally generated; that is, the contraction of a principal ideal in $S$ is principal in $R$.

Let $R$ be a commutative ring and $I\subset R$. If for every $x\in I$ and nonzero $r\in R\setminus I$, $xr\in I$, then $I$ is an absorbing subset of $R$.

In this talk the speaker will discuss $pgs$-extensions of commutative rings with identity, and its relation to absorbing subsets of rings.

PENN STATE ERIE
ERIE, PA
pxb39 at psu.edu

Idempotents in Generalized Matrix Rings

GARY F. BIRKENMEIER, University of Louisiana at Lafayette

In this talk, certain types of idempotents are investigated which determine specific classes of generalized matrix rings. Some of these classes properly contain the class of generalized triangular matrix rings. This is a preliminary report on joint work with Pham Ngoc Anh and Leon Van Wyk.

UNIVERSITY OF LOUISIANA AT LAFAYETTE
LAFAYETTE, LA
gfb1127 at louisiana.edu

Clean Rings for High School

VICTOR CAMILLO, University of Iowa

How I found idempotents at a high school mathematics competition that I graded for.

UNIVERSITY OF IOWA
IOWA CITY, IOWA
Victor-camillo at uiowa.edu

Unifying Strongly Clean Power Series Rings

ALEXANDER JAMES DIESL, Wellesley College

A ring is called strongly clean if every element can be written as the sum of a unit and an idempotent that commute with each other. Such rings can be viewed as a generalization of the classical strongly $\pi$-regular rings. In recent years, many authors have worked toward constructing and describing examples of strongly clean rings. In this talk, we will focus on the problem of determining when a power series ring is strongly clean.

WELLESLEY COLLEGE
WELLESLEY, MA
adiesl at wellesley.edu

HOM FUNCTOR COMMUTING WITH KAPPA-PRODUCTS

RADOSLAV DIMITRIC, CUNY-CSI

We define a class of modules satisfying a condition that Hom functors commute with $kappa$-products and examine its properties.

CUNY-CSI
NEW YORK, NEW YORK
rdimitric at juno.com

Negacyclic codes of length $2p^s$ over $\mathbb F_{p^m} + u\mathbb F_{p^m}$

HAI Q. DINH, Kent State University

For any odd prime $p$, the structures of all negacyclic codes of length $2p^s$ over the finite commutative chain ring $R=\mathbb{F}_{p^m} + u\mathbb{F}_{p^m}$ are established in term of their polynomial generators. When $p^m \equiv 1 \pmod 4$, $x^2+1$ is reducible as $(x+\alpha)(x-\alpha)$, then any negacyclic code $C$ of length $2p^s$ over $R$ is represented as a direct sum of a $-\alpha$-constacyclic and an $\alpha$-constacyclic codes of length $p^s$ over $\mathbb{F}_{p^m} + u\mathbb{F}_{p^m}$. In the remaining case, where $p^m \equiv 3 \pmod 4$, $x^2+1$ is irreducible, we proved that the ambient ring $\frac{R[x]}{\langle x^{2p^s}+1\rangle}$ is a local ring with maximal ideal $\langle x^2+1, u \rangle$, but it is not a chain ring. Such negacyclic codes were classified by categorizing the ideals of the local ring $\frac{R[x]}{\langle x^{2p^s}+1\rangle}$ into 4 distinct types. The detailed structures of ideals in each type were provided. Among other results, the number of codewords, and the dual of each negacyclic code are obtained.

KENT STATE UNIVERSITY
WARREN, OH
hdinh at kent.edu

On some left-right symmetric results on rings

DINH VAN HUYNH, Dept of Mathematics, Ohio University

We review and discuss some left-right symmetry results which have been obtained in recent years.

DEPT OF MATHEMATICS, OHIO UNIVERSITY
ATHENS, OH
huynh at ohio.edu

The Gabriel-Roiter measure and pure semisimple rings

NGUYEN VIET DUNG, Ohio University, Zanesville Campus

The Gabriel-Roiter measure, introduced by C. M. Ringel in 2005, is an invariant attached to finite length modules and has been studied extensively in recent years, mainly in the context of Artin algebras. In this talk, we discuss some applications of the Gabriel-Roiter measure in the study of left pure semisimple rings, i.e. rings $R$ such that every left $R$-module is a direct sum of finitely generated modules. In particular, when $R$ is a hereditary left pure semisimple ring with only two simple modules (the case where the pure semisimplicity conjecture is reduced to), we obtain a complete description (by recent joint work with José Luis García) of the Gabriel-Roiter measure of indecomposable left $R$-modules.

OHIO UNIVERSITY, ZANESVILLE CAMPUS
ZANESVILLE, OHIO
nguyend2 at ohio.edu

On Certain Classes of Semirings

FATMA AZMY EBRAHIM, Al-Azhar University, Egypt/The Ohio State University, Lima

In this work, we focus on the notions of regularity in semirings and many of their generalizations. Also we will determine several characterizations of them by their ideals or by their semimodules over them. Also, we examine some properties of right PπP-semirings, that is, semirings all of whose principal right ideal (for some positive integer ) are projective. It is shown that this class is a proper subclass of π-regular semirings.

AL-AZHAR UNIVERSITY
EGYPT,
fatema_azmy at hotmail.com

Two-parameter analogs of the Heisenberg enveloping algebra

JASON GADDIS, University of California, San Diego

The harmonic oscillator problem in quantum mechanics is to find operators $a$ and $b$ acting on a Hilbert space satisfying the relation $ab-ba=1$. This is one of the physical motivations behind studying the Weyl algebra and the enveloping algebra of the Heisenberg Lie algebra. In this talk, I will present a two-parameter version of this problem and discuss some of the subtleties in looking for simple, primitive factor rings in quantum enveloping algebras.

UNIVERSITY OF CALIFORNIA, SAN DIEGO
LA JOLLA, CA
jgaddis at ucsd.edu

Automorphism invariant modules

PEDRO ANTONIO GUIL ASENSIO, University of Murcia

Automorphism invariant modules.

UNIVERSITY OF MURCIA
MURCIA, SPAIN
paguil at um.es

Rings of definable scalars of some $sl_3(\mathbb{C})$-modules

SONIA L'INNOCENTE, University of Camerino

This a joint work with Mike Prest [LP2].

In the paper [H], Herzog investigated the ring of definable scalars of the finite-dimensional representations of the Lie algebra sl(2) of the 2x2 traceless matrices over the complex field. This is the ring of definable actions on the category of finite-dimensional sl(2)-modules that is, the ring to which the action of the universal enveloping algebra, U = U(sl(2)) on these modules extends in a definable way. Herzog showed, that this ring, denoted by U, is von Neumann regular and is a universal localisation of U. This work inspired further investigations, on rings of definable scalars of Verma modules [LP], on U(q)-modules (where q is not a root of unity) [HL].

It is natural to ask what happens when sl(2) is replaced by other simple Lie algebras, in particular by sl(3). We are able to obtain the similar results described by [H] if we restrict to the representations which are contained in, or whose dual is contained in, the natural representation of sl(3) on the polynomial ring on three generators.

References:

[H] I. Herzog, The pseudo-finite dimensional representations of $sl(2, k)$, Selecta Mathematica, 7 (2001), 241-290

[HL] I. Herzog, S. L'Innocente, The Nonstandard quantum plane, Annals of Pure and Applied Logic, 156 (2008), no. 1, 78-85

[LP] S. L'Innocente, M. Prest, Rings of definable scalars of Verma modules, Journal of Algebra and its Applications, 6 (2007), no. 5, 779-787

LP2] S. L'Innocente, M. Prest, Rings of definable scalars of some $sl_3(\mathbb{C})$-modules, In preparation

UNIVERSITY OF CAMERINO
CAMERINO, MACERATA
sonia.linnocente at unicam.it

Grassmanians, algebraic semigroup structures on cosets of the regular $Gl_n$ action, and their representations

MIODRAG C IOVANOV, University of Iowa

Row reduced matrices are one of the basic structures that are of unquestionable importance and have applications in many places outside of mathematics. It is perhaps less known (or used) that they are also closed under multiplication, and form a monoid. We show that the row reduced matrices are in fact characterized almost entirely by being set of representatives for the $Gl_n$ action, and closed under multiplication. We determine all such monoid structures - that we call annihilator semigroups, and show they are ``simultaneously echelonizable" and very close to row reduced matrices. This also allows one to view the total Grassmaniann G(n) on an n dimensional space as an algebraic semigroup, that is graded by a certain semigroup $\Pi$ whose $2^n$ elements are Young tableaux, and the graded components of G(n) are exactly the Schubert cells. Time permitting, we present other results on the structure of these annihilator semigroups, their classification up to isomorphism, the structure of their semigroup rings, and relations to other important mathematical objects as the plactic monoid and Young diagrams. This is joint work with Victor Camillo.

UNIVERSITY OF IOWA
IOWA CITY, IA
miodrag-iovanov at uiowa.edu

The Generalization of HNP ring, P-Bezout ring and 2-Bezout ring

IRAWATI, Institut Teknologi Bandung

We generalize HNP ring to M-HNP module, P-Bezout ring to P-Bezout module and 2-Bezout ring to 2-Bezout module. We also observe some properties of the generalization.

INSTITUT TEKNOLOGI BANDUNG
BANDUNG, WEST JAVA
irawati at math.itb.ac.id

Clean elements in certain ring extensions

PRAMOD KANWAR, Ohio University - Zanesville

An element $a$ of a ring $R$ is called clean if $a=e+u$ for some idempotent $% e$ and some unit $u$ in $R$. A ring is called clean if each of its elements is clean. It is known that the polynomial ring $R[x]$ over a ring $R$ is never clean and that the clean elements in a ring need not form a subring. We obtain set of clean elements in a polynomial ring and give conditions under which clean elements in a polynomial ring form a subring. Among other things it is shown that for a ring $R$, the set $Cl(R[x])$ of clean elements of $R[x]$ forms a subring of $R[x]$ if and only if $Cl(R)$ is a subring of $R$ and $Cl(R[x])=Cl(R)+N(R)[x]$ (where $N(R)$ is the upper nil radical) and that a positive solution to the Köthe's problem is equivalent to for any clean ring $R$, the set $Cl(R[x])$ of clean elements of $R[x]$ forms a subring of $R[x]$ if and only if $R/N(R)$ is a reduced ring. (This is a joint work with Andre Leroy and Jerzy Matczuk.)

OHIO UNIVERSITY - ZANESVILLE
ZANESVILLE, OHIO
kanwar at ohio.edu

On ideal-symmetric rings

TAI KEUN KWAK, Department of Mathematics/Daejin University

Lambek extended the usual commutative ideal theory to ideals in noncommutative rings, calling an ideal $A$ of a ring $R$ symmetric if $rst \in A$ implies $rts\in A$ for $r, s, t\in R$. $R$ is usually called symmetric if 0 is a symmetric ideal. This naturally gives rise to extending the study of symmetric ring property to the lattice of ideals. In the process we introduce the concept of an ideal-symmetric ring. We first characterize the class of ideal-symmetric rings and show that this ideal-symmetric property is Morita invariant. We provide a method of constructing an ideal-symmetric ring (but not semiprime) from any given semiprime ring, noting that semiprime rings are ideal-symmetric. We investigate the structure of minimal ideal-symmetric rings completely, finding two kinds of basic forms of finite ideal-symmetric rings. It is also shown that the ideal-symmetric property can go up to right quotient rings in relation with regular elements. The polynomial ring $R[x]$ over an ideal-symmetric ring $R$ need not be ideal-symmetric, but it is shown that the factor ring $R[x]/x^nR[x]$ is ideal-symmetric over a semiprime ring $R$.

DEWPARTMENT OF MATHEMATICS/DAEJIN UNIVERSITY
POCHEON,
tkkwak at daejin.ac.kr

Lifting von Neumann Regular Elements

T. Y. LAM, University of California, Berkeley

If $\,I\,$ is a left ideal in a ring $\,R\,$ and $\,a\in R\,$ is such that $\,a^2-a\in I$, can we find an idempotent $\,e\in R\,$ such that $\,a-e\in I$? The consideration of this important problem of ``lifting idempotents" has led to Nicholson's definition of ``suitable elements" and ``suitable rings". How about lifting (von Neumann) regular elements? That is, if $\,axa-a\in I\,$ for some $\,x\in R$, can we find a regular element $\,b\in R\,$ such that $\,a-b\in I$? In this talk, we'll report on some recent results in this direction. (This is joint work with Dinesh Khurana.)

UNIVERSITY OF CALIFORNIA
BERKELEY, CA
lam at math.berkeley.edu

s.Baer and s.Rickart Modules and an Associated Radical

RICHARD LOUIS LEBLANC, University of Louisiana at Lafayette

This is joint work with my advisor Gary F. Birkenmeier

In this talk, we present module theoretic definitions of the Baer and related ring concepts. We say a module is scalar Baer (Rickart), or s.Baer (s.Rickart), if the right annihilator of a nonempty subset (nonzero element) of the module is generated by an idempotent in the ring. We show that s.Baer and s.Rickart modules satisfy a number of closure properties such as submodules, extensions, and direct sums. Under certain conditions, a torsion theory is established for the class of s.Baer modules, and we provide examples of s.Baer torsion modules and modules with a nonzero s.Baer radical. The other principal interest of this presentation is to provide explicit connections between s.Baer and projective modules. Among other results, we show that every s.Baer module is an essential extension of a projective module. Additionally, we prove, with limited and natural assumptions, that in a generalized triangular matrix ring every s.Baer submodule of the ring is projective. Numerous examples are provided to illustrate, motivate, and delimit the theory.

UNIVERSITY OF LOUISIANA AT LAFAYETTE
LAFAYETTE, LA
rll1509 at louisiana.edu

Modules whose endomorphism rings are unit-regular

GANGYONG LEE, Sungkyunkwan University

Gangyong Lee$^*$ and Xiaoxiang Zhang (Sungkyunkwan University$^*$, Southeast University)

The notion of unit-regular rings was introduced by Ehrlich in 1968. Since then unit-regular rings have attracted wide interests and have been related to many other rings such as regular rings, morphic rings, clean rings, directly finite rings, rings having stable range 1, and rings having the internal cancellation property. In 2013, Lee, Rizvi, and Roman systematically investigated modules whose endomorphism rings are (von Neumann) regular. Recently, Lee, Roman, and Zhang considered the case in which the endomorphism ring of a module is a division ring. In between these two cases lies the study of modules whose endomorphism rings are unit-regular.

In this talk, we introduce the notion of a unit endoregular module as a module theoretic analogue for a unit-regular ring. A right $R$-module $M$ is called unit endoregular if its endomorphism ring is unit-regular. We discuss this notion and provide a number of characterizations and properties. For instance, unit endoregular modules satisfy the following basic properties: the substitution property, the cancellation property, the internal cancellation property, the directly finite property, the finite exchange property, the $C_2$ condition, the $D_2$ condition, and so on. In addition, every unit endoregular module is a morphic, (d-)Rickart, and clean module.

SUNGKYUNKWAN UNIVERSITY
SUWON, REPUBLIC OF KOREA, N/A
lgy999 at hanmail.net

Noetherian properties on generalized power series rings

JUNG WOOK LIM, Kyungpook National University

Let $D \subseteq E$ be an extension of commutative rings with identity, $I$ be a nonzero proper ideal of $D$, $(\Gamma, \leq)$ be a strictly totally ordered monoid such that $0 \leq \alpha$ for all $\alpha \in \Gamma$ and $\Gamma^*=\Gamma \setminus \{0\}$. Let $D+[\![E^{\Gamma^*, \leq}]\!]=\{f \in [\![E^{\Gamma, \leq}]\!] \mid f(0) \in D\}$ and $D+[\![I^{\Gamma^*, \leq}]\!] =\{f \in [\![D^{\Gamma, \leq}]\!] \mid$ the coefficients of nonconstant terms of $f$ belong to $I\}$. In this talk, we give some conditions for the rings $D+[\![E^{\Gamma^*, \leq}]\!]$ and $D+[\![I^{\Gamma^*, \leq}]\!]$ to be Noetherian or to satisfy the ascending chain condition on principal ideals.

KYUNGPOOK NATIONAL UNIVERSITY
DAEGU,
jwlim at knu.ac.kr

Semiprime Goldie Modules

MAURICIO GABRIEL MEDINA BÁRCENAS, Instituto de Matemáticas, Universidad Nacional Autónoma de México

All this work is developed in the context of the full subcategory $\sigma[M]$ of $R$-Mod. $M$ will be progenerator in $\sigma[M]$, except otherwise stated. In this talk will be considered modules with finite uniform dimension which satisfies ACC on annihilators and they will be called Goldie modules. Using the concept of semiprime module, it will be given the next characterization of semiprime Goldie modules:

Theorem 11   Let $M$ be an $R$-module progenerator in $\sigma[M]$ with finite uniform dimension. The following are equivalent:

1. $M$ is semiprime and non $M$-singular.
2. $M$ is semiprime and satisfies ACC on annihilators.
3. $M$ is essentially compressible.

Finally will be considered the case when $M$ is a duo module.

INSTITUTO DE MATEMáTICAS, UNIVERSIDAD NACIONAL AUTóNOMA DE MéXICO
MéXICO, DISTRITO FEDERAL
mauricio_g_mb at yahoo.com.mx

Traces on Semigroup Rings and Leavitt Path Algebras

ZACHARY MESYAN, University of Colorado

The trace on matrix rings, along with the augmentation map and Kaplansky trace on group rings, are some of the many examples of linear functions on algebras that vanish on all commutators. These examples can be generalized and unified by studying traces on (contracted) semigroup rings over commutative rings. It turns out that every such ring admits a minimal trace (i.e., one that vanishes only on sums of commutators), and the minimal traces on these rings can be completely classified. I will also discuss applications of this theory to various classes of semigroup rings and quotients thereof, including Leavitt path algebras.

This work was done jointly with Lia Vas.

UNIVERSITY OF COLORADO
COLORADO SPRINGS, CO
zmesyan at uccs.edu

On elements of minimal prime ideals

AHMAD MOJIRI, Saint Xavier University

E. Armendariz asked whether, in a general ring $R$, elements of minimal prime ideals were zero-divisors, in some sense. An example shows that the answer is ``no'' for left or right zero-divisors. An element $a\in R$ is a weak zero-divisor if there are $r,s\in R$ with $ras=0$ and $rs\ne 0$. It is shown that each element of a minimal prime ideal is a weak zero-divisor. Related questions are examined, in particular in rings where the set of nilpotent elements forms an ideal.

This is a joint work with W.D. Burgess and A. Lashgari.

SAINT XAVIER UNIVERSITY
CHICAGO, IL
mojiri at sxu.edu

Invertible Algebras With An Augmentation Map

JEREMY MOORE, Otterbein University

We briefly review some results about Invertible Algebras (algebras having bases that consist entirely of units) and other related notions. Then we consider the existence of an augmentation map as a possible way in which results about group rings, the archetypical invertible algebras, may be extended to more general settings. We also deal with the property that sets of inverses of linearly independent invertible elements be also linearly independent. We refer to algebras with this property as fluid algebras. We establish when finite field extensions are fluid algebras. Also we will show infinite field extensions are never fluid algebras. For any ring $R$, $M_2(R)$ is fluid. However, this does not extend to larger matrices. We define the $mojo$ of an $R$-algebra $A$ to be the largest number of linearly independent units in $A$, and denote this cardinal as $mojo(A)$. We then define the fluidity of an $R$-algebra $A$ to be the integer $n \leq mojo(A)$, such that for every set of $n$ or less linearly independent invertible elements, their inverses are also linearly independent. The fluidity of various families of algebras such as matrix rings and field extensions will be explored.
(This is joint work with Sergio López-Permouth.)

OTTERBEIN UNIVERSITY
PICKERINGTON, OHIO
jmoore at otterbein.edu

On some kinds of derivations in BCI-algebras

GHULAM MUHIUDDIN, University of Tabuk, Tabuk 71491, Saudi Arabia

In the present paper we establish some results on (regular) generalized left derivation in a BCI-algebra X and study related properties. Furthermore, we investigate the concept of a F-invariant generalized left derivation and discuss some examples. Using this concept a condition for a generalized left derivation to be regular is provided. Finally, some results on p-semisimple BCI-algebra are established.

UNIVERSITY OF TABUK, TABUK 71491, SAUDI ARABIA
TABUK, TABUK
chishtygm at gmail.com

On Uniserial Dimension

ZAHRA NAZEMIAN, Isfahan University of Technology

‎We define and study a new dimension‎, ‎which we‎ call uniserial dimension‎, to measure how far away modules are form being uniserial‎. ‎‎It is shown that for a ring $R$ and an ordinal number‎ ‎$\alpha$‎, ‎there exists an $R$-module of uniserial dimension $\alpha$‎. ‎We show that a commutative ring $R$ is Noetherian (resp‎. ‎Artinian)‎ ‎if and only if every finitely generated $R$-module has (resp‎. ‎finite) uniserial dimension ‎if ‎and ‎only ‎if ‎‎ the ‎right ‎module‎ $R \oplus R$ has (resp‎. ‎finite) uniserial dimension. ‎Rings‎ ‎whose modules have uniserial dimension are characterised. ‎In fact‎, ‎it is shown that every right $R$-module has uniserial dimension if ‎ and only‎ ‎if the‎ ‎free right $R$-module $\oplus _{i = 1}^{\infty } R$ has uniserial dimension if and only if $R$ is a semisimple Artinian ring‎.‎ ‎

ISFAHAN UNIVERSITY OF TECHNOLOGY
ISFAHAN, IRAN
z.nazemian at math.iut.ac.ir

Rings where principal left ideals are principal annihilators

WILLIAM KEITH NICHOLSON, University of Calgary

The rings of the title are studied. It is shown that, every finitely generated left ideal is a principal left annihilator, and the only one with zero right annihilator is the ring itself. With this the semiprime examples are characterized (all semisimple), and those with the ACC on principal left annihilators are investigated.

UNIVERSITY OF CALGARY
CALGARY, ALBERTA
wknichol at ucalgary.ca

Idempotent lifting properties

PACE P. NIELSEN, Brigham Young University

Several results in the literature focused on lifting idempotents are improved, by either removing the lifting hypothesis or weakening other assumptions. For instance we prove that countable sets of idempotents, which are orthogonal modulo an enabling ideal, lift to orthogonal idempotents. Left associates of liftable idempotents also lift modulo the Jacobson radical. Additionally, we exhibit situations when half-orthogonal sets of idempotents can be orthogonalized by multiplying by a unit. These results have implications on the structure of Harada modules.

BRIGHAM YOUNG UNIVERSITY
PROVO, UT
pace at math.byu.edu

Commutative rings whose multiplicative endomorphisms are power functions

GREGORY GRANT OMAN, University of Colorado, Colorado Springs

Let $R$ be a commutative ring. For any positive integer $m$, the power function $f:R\rightarrow R$ defined by $f(x):=x^m$ is easily seen to be an endomorphism of the multiplicative semigroup $(R,\cdot)$. In this talk, we characterize the commutative rings $R$ with identity for which every multiplicative endomorphism of $(R,\cdot)$ is equal to a power function. Open questions will also be presented.

UNIVERSITY OF COLORADO, COLORADO SPRINGS
COLORADO SPRINGS, COLORADO
goman at uccs.edu

Compatible Ring Structures II

BARBARA L OSOFSKY, Rutgers University (Emerita)

In my paper Compatible Ring Structures on Injective Hulls of Finitely Embedded Rings, Contemporary Mathematics 609 (2014) pages 245-266, I characterized when an appropriate submodule $M_{R}$ of the injective hull $E_{R}$ of a finitely embedded ring $R$ has a ring structure extending ring multiplication on $R_{R}$ to a ring structure on $M_{R}$. I show that $M_{R}$ has such a compatible ring structure iff every simple right $\mathrm{End}_{R}\left( \mathrm{Soc}\left( R_{R}\right) \right) _{R}$-module has a simple right $R$-socle.

In this talk I restrict my rings to be artinian (where $E=M$) to be able to use standard techniques of qF rings and Morita duality instead of having to make some not so familiar definitions to obtain the characterization. I sketch a proof by analyzing exactly how and why the proof in the above paper works, and observing a restatement of the classification to get Theorem: Let $R$ be a right artinian ring, $E=E\left( R_{R}\right)$, $\Lambda =\mathrm{End}_{R}\left( E\right)$, $\widetilde{\Lambda }=\Lambda \left/ J\left( \Lambda \right) \right.$. Then $E$ has a ring structure compatible with $R$-module multiplication on $E_{R}$ iff for every simple factor ring $\widetilde{\Lambda }_{S}$ of $\widetilde{\Lambda }$, $\left( \widetilde{\Lambda }_{S}\right) _{R}$ is a rational extension of its $R$-socle.

A copy of my Contemporary Math paper can be found at
https://www.dropbox.com/s/j3d0vfx190xts3o/conm12128.pdf

A preliminary version of my presentation slides can be found at
https://www.dropbox.com/s/3wpo5tqy0w38bkn/comp-ring-structures-Columbus2014.pdf

RUTGERS UNIVERSITY (EMERITA)
NEW BRUNSWICK/PISCATAWAY, NEW JERSEY
osofskyb at member.ams.org

Baer and Rickart Hulls of Modules

JAE KEOL PARK, Department of Mathematics, Pusan National University

Since the discovery of the existence of the injective hull of an abitrary module $M$, the notion of ``hull" of $M$ or a unique smallest essential overmodule with some specific properties has been of interest. Kaplansky introduced the notions of Baer and Rickart rings in 1950's. Thsese classes of rings, which happen to have their roots in Functional Analysis, were extensively studied by Kaplansky, Berberian and many others. In recent years, by Lee, Rizvi, and Roman, the notions of a Baer and a Rickart rings were extended to analogous module theoretic notions using the endomorphism ring of the module under consideration.

While some work has been done on the existence of the quasi-Baer ``ring hull" of a ring $R$ for certain classes of rings by Birkenmeier, Park, and Rizvi, there is almost nothing known about a Baer or a Rickart ``module hull" of a module $M$. In this work, for a given module $M$ and a fixed injective hull $E(M)$, we investigate the existence of a Baer hull and a Ricaket hull over commutative rings. It is shown that a Baer module hull (or Rickart module hull) may not exist in general. We obtain certain classes of modules for which Baer modules hulls or Ricakrt module hulls do exist. Explicit descriptions of each type of hulls of $M$ are described for these classes of modules. We exhibit differences between a Baer module hull from that of a Rickart module hull by providing explicit examples and related results. We also compare Baer hulls and extending hulls of certain classes of modules.

It is well-known that direct sum of Baer (or Rickart) modules do not always inherit the repective property. As an application, we construct Baer and Rickart module hulls of some direct sums which are not Baer (or Rickart) themselves.

(This is joint work with S. Tariq Rizvi.)

DEPARTMENT OF MATHEMATICS, PUSAN NATIONAL UNIVERSITY
BUSAN 609-735,
jkp1128 at yahoo.com

Leavitt Path Algebras with Bases Consisting Solely of Units

NICK PILEWSKI, Ohio University

Following López-Permouth, Moore and Szabo, given a ring $R,$ an $R$-algebra $A$ is called an invertible algebra if it has an $R$-basis of units in $A.$ Leavitt path algebras are generalizations of the classical Leavitt algebras, the universal examples of algebras without the Invariant Basis Number property. In this talk, we report on the search for a condition on the graph $E$ which is equivalent to the Leavitt path algebra $L_K(E)$ being an invertible algebra for any field $K \neq \mathbb{F}_2.$ Leavitt path algebras with coefficients in $\mathbb{F}_2$ and other commutative rings are also considered. (This is a joint work with Sergio López-Permouth.)

OHIO UNIVERSITY
ATHENS, OH
np338697 at ohio.edu

On Irreducible Representations of Leavitt path algebras

KULUMANI RANGASWAMY, University of Colorado, Colorado Springs

Given an arbitrary graph E and a field K, we indicate new methods of constructing simple left modules over the Leavitt path algebra L(E). The corresponding primitive ideals are described. The cardinality of single isomorphism class of simple modules isomorphic to a given simple L-module is computed. Other consequent results are outlined.

UNIVERSITY OF COLORADO, COLORADO SPRINGS
COLORADO SPRINGS, CO
ranga at uccs.edu

Affine tropical varieties

LOUIS ROWEN, Bar-Ilan University

An affine tropical variety can be defined as the intersection of the simultaneous root set of a finite number of tropical polynomials. We consider the tropical dimension and related invariants in terms of the algebraic structure, bearing in mind that the underlying algebraic structure is a semifield rather than a field. Special attention is paid to ``nonstandard'' tropical varieties.

BAR-ILAN UNIVERSITY
RAMAT-GAN,
rowen at math.biu.ac.il

On pseudocomplements and supplements in the big lattice of preradicals.

MARTHA LIZBETH SHAID SANDOVAL MIRANDA, Facultad de Ciencias, UNAM

In this talk, we will consider aspects of the big lattice of preradicals, related to pseudocomplements and supplements. Also, we will consider essential preradicals and superfluous preradicals, and we will characterize the situation in which all nonzero preradicals are essential as well as the one in which all proper preradicals are superfluous.

FACULTAD DE CIENCIAS, UNAM
MEXICO CITY, MEXICO D.F.
marlisha at gmail.com

Posets of increasing complexity

MARKUS SCHMIDMEIER, Florida Atlantic University

We consider a family of double-infinite posets of width at most three such that the module categories of their incidence algebras are naturally contained in each other and grow slowly in complexity.

Symmetries of the posets give rise to endofunctors for the module categories: The reflection at the center to the duality; the rotation to the square of the Auslander-Reiten translation; and the shift to the graded shift.

The categories are equivalent to lattices over tiled orders studied by W. Rump and -- modulo the projectives on one orbit under the graded shift -- to invariant subspaces of nilpotent linear operators.

FLORIDA ATLANTIC UNIVERSITY
BOCA RATON, FL
markus at math.fau.edu

Dual Preserving Maps for Linear Codes over Finite Frobenius Rings

STEVE SZABO, Eastern Kentucky University

Dual Preserving Maps for Linear Codes over Finite Frobenius Rings.

EASTERN KENTUCKY UNIVERSITY
RICHMOND, KENTUCKY
steve.szabo at eku.edu

Making the local global in Leavitt path algebras

LIA VAS, University of the Sciences

We adapt the direct finite condition (i.e $xy=1$ implies $yx=1$) for unital rings to rings with local units and characterize directly finite Leavitt path algebras as exactly those having the underlying graphs in which no cycle has an exit. Our proof involves consideration of ``local'' Cohn-Leavitt subalgebras of finite subgraphs and we illustrate that this idea transends the consideration of direct finiteness alone.

UNIVERSITY OF THE SCIENCES
PHILADELPHIA, PA
l.vas at usciences.edu

Revisiting Farrell's nonfiniteness of Nil

KUN WANG, The Ohio State University

We study Farrell Nil-groups associated to a finite order automorphism of a ring $R$. We show that any such Farrell Nil-group is either trivial, or infinitely generated (as an abelian group). Building on this first result, we then show that any finite group that occurs in such a Farrell Nil-group occurs with infinite multiplicity. If the original finite group is a direct summand, then the countably infinite sum of the finite subgroup also appears as a direct summand. We use this to deduce a structure theorem for countable Farrell Nil-groups with finite exponent. Finally, as an application, we show that if $V$ is any virtually cyclic group, then the associated Farrell or Waldhausen Nil-groups can always be expressed as a countably infinite sum of copies of a finite group, provided they have finite exponent (which is always the case in dimension 0).This is joint work with Jean-François Lafont and Stratos Prassidis.

THE OHIO STATE UNIVERSITY
COLUMBUS, OHIO
kwang at math.ohio-state.edu

Covering Numbers of Finite Rings

NICHOLAS J WERNER, The Ohio State University-Newark

Any finite non-cyclic group $G$ is equal to a union of its proper subgroups. The covering number of $G$ is the minimum number of subgroups necessary to cover $G$. Covering numbers are known for several classes of finite groups, and the computation covering numbers is a problem of current interest.

In this talk, we discuss the analogous question for finite rings. In general, not much is known. We say that a finite (associative, unital) ring $R$ is coverable if it is equal to a union of its proper subrings, and the covering number of $R$ is the minimum number of subrings required to cover $R$. Not every finite ring is coverable, and it is nontrivial to decide whether $R$ is coverable. We present a classification theorem for finite coverable semisimple rings, and determine the covering number for $R$ when $R$ is coverable and equal to a direct product of finite fields.

THE OHIO STATE UNIVERSITY-NEWARK
NEWARK, OH
nwerner at newark.osu.edu

Automorphisms of Additive Codes

JAY A. WOOD, Western Michigan University

An additive code over a finite field $\mathbb{F}_q$ is an additive subgroup $C \subset \mathbb{F}_q^n$. Define the monomial group $\operatorname{Monom}(C )$ to be all the monomial transformations of $\mathbb{F}_q^n$ that map $C$ to $C$. Define the Hamming isometry group $\operatorname{Isom}(C )$ to be all the additive isomorphisms of $C$ that preserve Hamming weight. Any monomial transformation of $\mathbb{F}_q^n$ preserves the Hamming weight on $\mathbb{F}_q^n$. Thus, there is a natural restriction homomorphism

$$\operatorname{restr} : \operatorname{Monom}(C ) \rightarrow \operatorname{Isom}(C ).$$

When the field $\mathbb{F}_q$ is a prime field, the restriction map is always onto. However, when the field $\mathbb{F}_q$ is not a prime field, the two groups

$$\operatorname{restr}(\operatorname{Monom}(C )) \subset \operatorname{Isom}(C )$$

can be as different as one chooses (subject to a closure property). In particular, there are additive codes $C$ for which $\operatorname{restr}(\operatorname{Monom}(C ))$ equals $\mathbb{F}_q^\times \cdot \operatorname{id}_C$ (minimum possible), while $\operatorname{Isom}(C )$ equals the group of all additive isomorphisms of $C$ (maximum possible).

WESTERN MICHIGAN UNIVERSITY
KALAMAZOO, MI
jay.wood at wmich.edu

On certain operators in modular meet-continuos lattices

LUIS ÁNGEL ZALDÍVAR-CORICHI, IMATE-UNAM

Abstract: Given a complete modular meet-continuous lattice $A$, an inflator over $A$ is a monotone function $d:A\rightarrow A$ such that $a\leq d(a)$ for all $a\in A$. If $I(A)$ is the set of all inflators over $A$, then $I(A)$ is a complete lattice. Motivated by preradical theory we introduce two operators, the totalizer and the equalizer over $I(A)$. In this talk we will obtain some properties of these operators and see how are they related to the structure of the lattice $A$.

IMATE-UNAM
MéXICO CITY, DISTRITO FEDERAL
angelus31415 at gmail.com

A Decomposition Theorem of Linear Transformations

YIQIANG ZHOU, Memorial University of Newfoundland

We talk about how to express a linear transformation as a sum of two commuting invertible linear transformations.

References

[1] D. Zelinsky, Every linear transformation is a sum of nonsingular ones, Proc. AMS. 5(1954), 627-630.

[2] G.Tang and Y. Zhou, When is every linear transformation a sum of two commuting invertible ones?, Linear Algebra Appl., 439(2013), 3615-3619.

MEMORIAL UNIVERSITY OF NEWFOUNDLAND
ST.JOHN'S,
zhou at mun.ca

Differential polynomial rings over locally nilpotent rings need not be Jacobson radical

MICHAL ZIEMBOWSKI, Politechnika Warszawska

At the 2011 conference held in Coimbra entitled ``Non-Associative Algebras and Related Topics'', I. P. Shestakov asked the following.

Question: Let $R$ be a locally nilpotent ring with a derivation $D$ and let $S = R[X; D]$ be the differential polynomial ring. Is the Jacobson radical of $S$ equal to $S$?

We answer this question in the negative. This is a joint work with Agata Smoktunowicz.

POLITECHNIKA WARSZAWSKA
WARSAW, POLAND
m.ziembowski at mini.pw.edu.pl