The amplitude of a wave
We have seen that waves have a wavelength \( \lambda \): the distance between its crests. We are now interested in the height of the wave. This height is called the amplitude, and is usually denoted by the symbol \( A \).
Waves with larger amplitude are stronger. Thus consider tuning your radio to a station broadcasting at a given wavelength. If the signal is strong and clear, it means that the radio waves have a large amplitude; if the signal is weak, the waves have a small amplitude.
Our question now is: how much can the amplitude be? The answer will lead us to the second crucial lesson of quantum theory.
The second lesson of quantum mechanics
In classical physics, we had electromagnetic waves. It was believed that these waves could have any amplitude \( A \) from zero to infinity.
But surprisingly, the actual situation turned out to be different. This difference can be detected if our experiments are precise enough to detect quantum effects.
Let us fix the wavelength \( \lambda \) of an electromagnetic wave and imagine reducing the amplitude.
Once we get down to small values of the amplitude, we find something unexpected. We find that the amplitude cannot be reduced below a certain minimum value.
In fact more is true. The next stronger wave is twice as strong as the minimum wave. More precisely, the energy of this next stronger wave is twice the energy of the minimum strength wave.
The full story is as follows. Let the weakest allowed wave have energy \( E \). Then the allowed amplitudes are such that the energies can be \( E, 2E, 3E, \dots\). But we cannot get an energy like \( .7 E\) or \( 1.6 E\). Thus the allowed strength of the wave is discrete rather than continuous.
The difficulty of noticing discreteness
This discreteness is a fundamental fact of quantum theory. But why was this discreteness of energy not noticed earlier, in the days of classical physics?
The reason is that the minimum energy \( E\) is typically very small for wavelengths of interest. As an analogy, consider a cubical building made of concrete. At first we might think that the building can have any height. But this is not really true. The height of the building could be a billion atomic layers. We can add one extra layer of atoms to make the building taller, but we cannot add half an extra layer. However, we do not normally notice this discreteness of the height since an atomic layer is so thin compared to the height of a typical building.
Similarly, the radio waves that were generated in the early days were much stronger than the minimum energy \( E \) allowed for their wavelength, and so the discreteness of energy was not noticed.
"Particle like" behavior
The discreteness of the strength of the electromagnetic waves is sometimes called the 'particle like behavior of the electromagnetic wave'. This nomenclature can be a little confusing, because we are not saying that the wave is a pointlike object like a particle. What happened was that scientists had already becomes used to the fact that particles were discrete: they had noticed that we can have no electrons or one electron, but we cannot have half an electron. So when they found that the electromagnetic wave was showing a similar discrete behavior, they called it a 'particle like behavior of the wave'.
To emphasize this 'particle like' discreteness of the electromagnetic wave, the minimum strength electromagnetic wave was called a photon. This name is similar to the names used for the entities which used to be considered particles: electron, proton, neutron etc.
The discreteness of the electromagnetic wave was conjectured by Max Planck.
Summary
In classical physics we had two kinds of entities: particles and waves. Quantum theory brought two changes to this picture:- Particles like electrons were actually waves; these waves could be made to cancel just like electromagnetic waves.
- Electromagnetic waves exhibited a discreteness in their strength; we can call this discreteness a 'particle like behavior' in the sense that half a photon is disallowed just like half an electron is disallowed.
Thus there is just one kind of entity in quantum theory, and this entity inherits features from each of the two entities in classical physics. Each object - photon or electron - has the form of a wave, and this wave exhibits the discreteness expected of particles.
The next question is: how much is the minimum energy \( E \) of a photon?
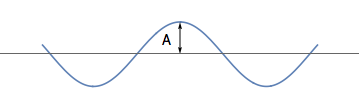
The maximum height of the wave from its mean position is called the amplitude \( A \).
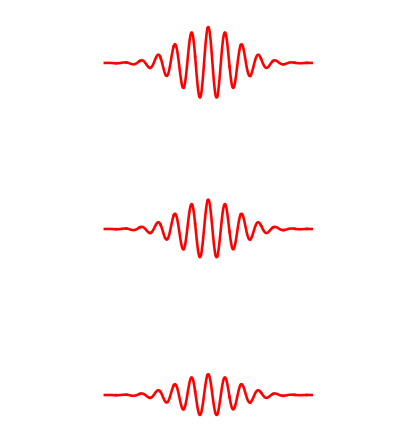
The amplitude of an electromagnetic wave goes in discrete steps. The lowest wave has energy \( E \), the middle one has energy \( 2E\), the upper one has energy \( 3E\). The wave with energy \( E \) is called one 'photon'.