Correlations
Suppose we have independent wavefunctions for an electron and a proton. Let us again take these wavefunctions to each have the form of two well separated and equal bumps: one on the left and one on the right.
Since the two wavefunctions are not related with each other in any way, the electron and the proton are uncorrelated. This means that the probabilities for different locations of the electron-proton pair are given by the simply multiplying of the appropriate probability for the electron with the appropriate probability for the proton. Thus the probability that the electron is on the left and the proton is on the right is given by \( \frac{1}{2} \times \frac{1}{2} =\frac {1}{4} \).
Now consider our example where the electron and proton form an atom. Now the states of the electron and proton are correlated: if the electron is on the left then the proton is on the left, and if the electron is on the right then the proton is on the right.
Now the probabilities cannot be given by multiplying a probability for the electron and a probability for the proton.Entangled states
States with such a correlation are called entangled states. Alternatively, we can say that the state of the electron is entangled with the state of the proton.
We can see that entangled states are going to be much more common than non-entangled states. Consider the electron-proton system. A general state for this system is depicted in fig.3: we can choose any waveform over the 2-dimensional \( x_1-x_2 \) plane. In general such a state will have some correlation between the positions of the electron and the proton. Thus the states with no correlation will be a special small subclass; i.e., entanglement is more the rule than the exception.
What causes entanglement?
To motivate the entangled state of fig.2, we had used the fact that the electron and proton tend to bind together into an atom; this binding correlated the positions of these two particles. One may therefore ask the question: is there a relation between force and entanglement?
The answer can be given in two parts. First, entanglement is just a correlation between the states of two (or more) particles, and so by itself it does not have anything to do with a force. We can consider any state for a quantum system, and so we consider an uncorrelated state or a correlated state.
But the second point to note is that in practice, forces often cause uncorrelated particles to get correlated. Suppose two particles are initially un-entangled, and then happen to drift near each other. They may then attract or repel each other due to some force. This attraction or repulsion creates a correlation between the positions of the particles, so the overall state of the two particles becomes an entangled one.
We will now see that the process of detecting particles involves exactly this kind of generation of entanglement. This fact will be crucial to resolving the puzzle of randomness in quantum measurements.
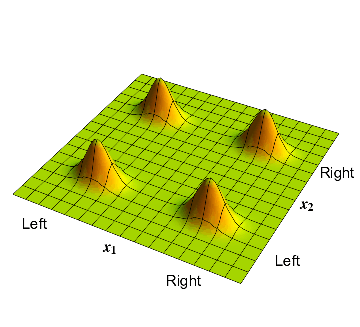
The electron and proton positions are not correlated: each possibility (left or right) for the electron is allowed, and so is each possibility for the proton.
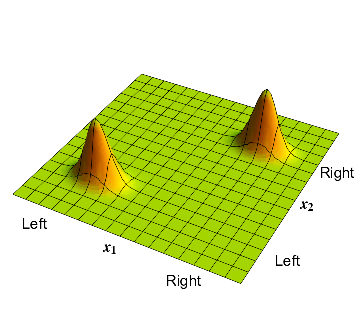
The electron and proton positions are correlated: the proton can be on the left or right, but the electron has to be at the sane location.
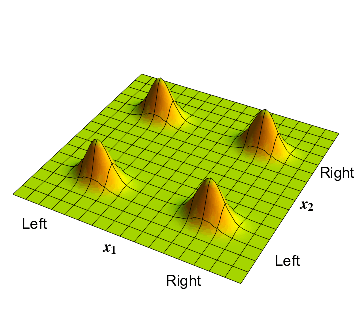
Initially the electron and proton are uncorrelated. The electrostatic attraction pulls the electron towards the proton (the proton is heavy and so hardly moves). The resulting state thus has correlations between the particles; i.e., it is an entangled state.