 Black holes: A first pass
Black holes: A first pass 
 Black holes: A first pass
Black holes: A first pass 
The central idea behind black holes is the notion of trapping. Can there be a region of space where one can go in, but from which one cannot come out? Such a region is called a black hole.
Why should we think such regions might exist? The reason is gravity. Gravity is a universal force that makes everything attract everything else. If we put a lot of mass in some region, then any object coming near this region will be strongly pulled in by the gravitational attraction created by this mass. The question then is: Can this gravitational force trap objects that fall in, so that they can never come out?
Quite remarkably, the answer to this question has changed each time we have incorporated a new principle of physics in our thinking. It is likely that the best way to arrive at a final theory unifying all principles is to look for a consistent description of the black hole. The theory of black holes is therefore the cutting edge of research into the ultimate laws of nature.
The story of black holes has gone through 4 iterations. In each new iteration, we incorporate a new principle of physics, and find a change in what can and cannot be trapped.

The term 'black hole' was coined by John Wheeler in 1967
We assume that:
Using these principles, John Michell conjectured in 1783 that sufficiently massive stars may be invisible: the gravitational pull of the body may be so strong that even light cannot escape from their surface and reach our eyes. He called such objects dark stars.
Today we have learnt that nothing can travel faster than the speed of light. If we add this assumption to our Newtonian thinking, then it would seem that nothing can fly out of a dark star. Are such dark stars therefore black holes?
It turns out the answer is no. Even though light and other objects may not be able to fly out on their own from such dark stars, they can still be extracted out by applying a suitable force. Consider a person standing on such a star. He cannot jump up and escape the gravitational pull of the star. But he can sit in a rocket, and the thrust provided by the rocket can lift him out to empty space, away from the star.
Thus we see that with Newtonian physics, nothing is really 'trapped' by gravity, and we cannot get a black hole.
The situation changed with the work of Einstein.

John Michell ,
1724-1793.

A normal star emits light.
 Michell argued that light will not be able to escape the gravity of a sufficiently massive object, so we will get a 'dark star'.
Michell argued that light will not be able to escape the gravity of a sufficiently massive object, so we will get a 'dark star'.

But the dark star is not a black hole, since an object (the black dot) can still be extracted away from the star using the force supplied by a rocket.
We assume that:
In this theory the curvature of spacetime can be made such that we get a trapping region: i.e. we get a black hole. There is a boundary surface called the horizon: things can fall in through the horizon, but they cannot come out. In fact more is true: once things fall through the horizon, they must keep moving towards the center of the hole, where they eventually get crushed at a location called the singularity.
When stars run out of the fuel they can burn, they start to compress under their own gravitational attraction. Computations show that if a star is more than 3 times heavier than the sun, then it would compress in a runaway fashion. That is, it would get more and more dense as it compresses, till it becomes an infinite density point which forms the singularity. This process is called the gravitational collapse of the star, and it results in the formation of a black hole.
The existence of such black holes marked a very unusual step in the development of physics. In Newton's world (first iteration) anything which could be done could be undone: for example we could collect many atoms together to make a planet, but we could then also prise these atoms apart to break the planet back to individual atoms. By contrast, in general relativity (second iteration) we can make a black hole by throwing a lot of matter together into a region. But we can never 'unmake' the hole, since nothing that went in the hole can ever come out.
While this irreversibility of black hole formation is a strange phenomenon, it is not in contradiction with anything. Thus general relativity is a consistent theory on its own, and this theory predicts the existence of black holes which trap anything that falls into them.
We will find a serious problem, however, at the next iteration.

In 1915 Albert Einstein argued that Newton's law of gravitation should be replaced by a more accurate theory: General Relativity

A typical star (the dark disc) creates a gentle curvature of spacetime

Allowing more curvature eventually leads to a black hole. The exterior of the hole, depicted above, ends in a horizon (the green circle); anything falling past the horizon cannot come back out.
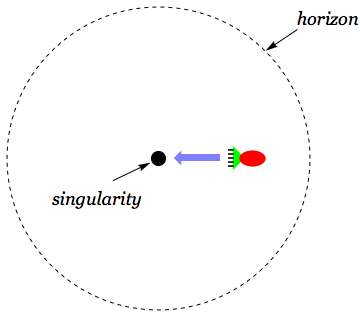
A schematic picture of the black hole interior. Even a rocket trying its best to fly outwards will get dragged back into the singularity and be crushed.
We assume that:
With this setup, Hawking made two remarkable discoveries, in 1974 and 1975.
In 1974 Hawking found that due to quantum mechanical effects, the black hole slowly leaked out energy in the form of long wavelength radiation. This radiation is called Hawking radiation, and it leads to a slow evaporation of the hole. We can think of mass and energy as equivalent notions, due to Einstein's relation \( E=mc^2 \). Thus the leakage of energy in the form of Hawking radiation leads to a slow decrease in the mass of the hole, and Hawking concluded that the hole would eventually disappear. So in this third iteration, we cannot trap mass (or equivalently, energy)
The radiation emerging from the black hole has a strange property: it does not carry the information of the matter that made the black hole in the first place. The reason for this is simple: the radiation is produced at the horizon, while the matter which made the hole has been sucked away to a different location - the central singularity.
In 1975 Hawking showed that this situation leads to a very serious problem, as follows:
This problem is called the Black hole information paradox. The reason it is a paradox is that in all formulations of physics considered before, information was not lost. For example in Newtonian physics, we may start with particles in one configuration and after some time end with a different configuration; but we can always look at the final configuration and figure out exactly which initial configuration it came from. Similarly, in quantum theory we start with an initial wavefunction, and this evolves to a final wavefunction; but we can look at the final wavefunction and know which initial wavefunction it came from. Thus information is never lost in normal physical processes; it just gets pushed into different forms.
But in the Hawking process we have seen that we cannot look at the final wavefunction (describing radiation) and say which initial wavefunction (i.e. which star) it came from. Thus, Hawking argued, the process of black hole formation and evaporation cannot be described by the usual rules of quantum theory; i.e., black holes violate quantum mechanics.
Most people were unhappy with this conclusion, since they did not want to give up quantum theory. But they could not find anything wrong with Hawking's computation of radiation or the fact that this radiation carried no information about the hole. Many people therefore accepted the simplest possible way out: the existence of remnants; defined as follows.
Remnants: Suppose we accept Hawking's assumptions and computations when the black hole is large. But when the black hole is about to vanish, it will be vey small, and for such small black holes the gravity theory should also be modified to include quantum effects; i.e., we should replace Einstein's general relativity by a theory of quantum gravity. It may then happen that some (heitherto unknown) effect in this quantum gravity theory stops the further evaporation of the hole, so that we are left with a tiny remnant. In that case the information that went into the hole (e.g. the composition of a collapsing star) would not be lost, but would instead stay trapped forever in this tiny remnant. We will therefore avoid a conflict with the foundations of quantum theory.
To summarize, in this third iteration we find that mass (or equivalently, energy) is not trapped, while information is either lost or trapped, depending on our assumptions about the endpoint of black hole evaporation.Surprisingly, the picture of the black hole was to change once again.

Stephen Hawking argued in 1975 that the dynamics of black holes violates quantum theory.
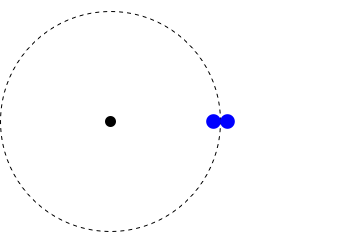
The Hawking evaporation process. Quantum effects create a particle-antiparticle pair near the horizon. One member of the pair escapes as radiation, while the other falls into the hole. Since the radiation carries away energy, the hole becomes smaller.
The information paradox: we cannot look at the final state of radiation and say which star we started with; thus information has been 'lost'.
The remnant idea: the evaporation leaves a tiny remnant which stores the needed information.
We assume that:
Computations with string theory indicate that we get a remarkable change in the dynamics of the hole once again: the hole takes the form of a fuzzball, which traps neither energy nor information. A fuzzball is in principle just like a planet, which also does not trap energy or information.
In a planet, the region inside its surface is filled with a complicated structure of atoms, which carry the 'information' about the planet. A fuzzball also has a complicated structure inside its boundary, and this structure carries the information of the fuzzball. The idea that all black holes are replaced by fuzzballs in quantum gravity is called the fuzzball paradigm.
Since we had defined a black hole as something which creates 'trapping', strictly speaking we should say that there are no black holes in string theory. But interestingly, fuzzballs retain several properties of the traditional black hole (i.e. the black hole that we had in the third iteration). The radius of the typical fuzzball is approximately the same as the horizon radius of the black hole with the same mass. The gravity felt by a particle outside the fuzzball boundary is approximately the same as the gravity outside the horizon of the black hole. Further, the fuzzball emits radiation at the same temperature that Hawking found for his radiation from the traditional black hole. For these reasons we sometimes refer to fuzzballs as being the 'actual states of black holes in string theory'.
Resolution of the information paradox: The crucial fact is that with fuzzballs, there is no black hole information paradox. Consider again the gravitational collapse of a star made of Hydrogen and a star made of Helium. Even though these two stars may have the same total mass, the detailed internal structure of the fuzzballs they create will be different. This difference gets imprinted on the radiation produced by the fuzzballs. Thus when the fuzzballs evaporate away, we can look at the final radiation and know all the information about the star we had started with.
By contrast, in the third iteration the black hole was was 'empty' except for a central singularity. Thus the hole was described only by its spacetime curvature, which did not have any information about the initial star apart from its total mass. Since the radiation was produced by this curvature, it could not carry any information, and we had a paradox.
Non-triviality of the fuzzball paradigm: Since fuzzballs do not create an information problem, one might wonder why people did not seek a fuzzball-like structure right away, instead of worrying about the paradox created by the traditional black hole. The reason is that with ordinary matter, it is impossible to make a horizon sized object that does not collapse under the pull of its own gravity. It is the unique features of string theory: extra dimensions, extended objects like strings and branes etc. that allow for the back hole to get replaced by a fuzzball and resolve the information problem.
Alternative proposals: A very satisfying aspect of the fuzzball paradigm is that it resolves the information paradox without violating any of the fundamental principles of relativity or quantum theory. Alternative resolutions of the paradox have also been proposed, where the traditional structure of the hole is left essentially unchanged; i.e., there is a horizon, and the all the matter inside the horizon has been collapsed to a highly dense ball at the center. In these alternative proposals one typically solves the problem by violating one of the familiar tenets of physics: causality (the principle that nothing can travel faster than light), locality (the principle that objects at one point can directly influence only the things in their immediate vicinity) or quantum unitarity (the evolution rule in quantum theory which says that states do not appear or disappear during time evolution).
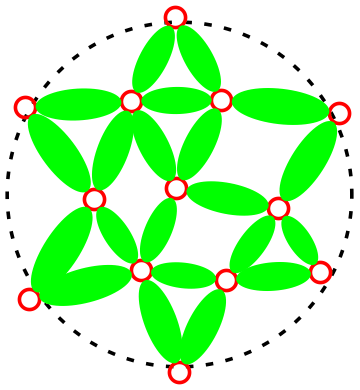
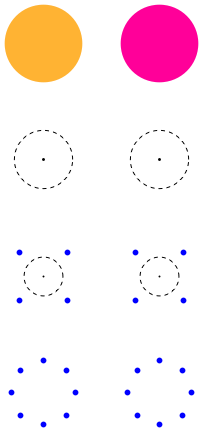
A fuzzball is a horizon sized structure that does not collapse because of special features of string theory. The red circles depict 'holes' in space and the green bubbles are spheres that join them. Such configurations result from novel topologies which arise because of the extra dimensions in string theory.
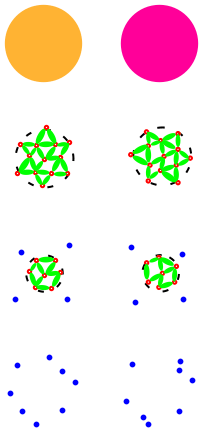
How fuzzballs resolve the information paradox: different stars give different fuzzball structures, and thus different radiation. We can then look at the final radiation and know which star we started with.

in 1959 Buchdahl proved that a spherical ball of normal matter will collapse to a black hole if its radius is shrunk below 1.25 times the horizon radius. Fuzzballs bypass this theorem and resist collapse because string theory allows novel structures not possible with ordinary matter.
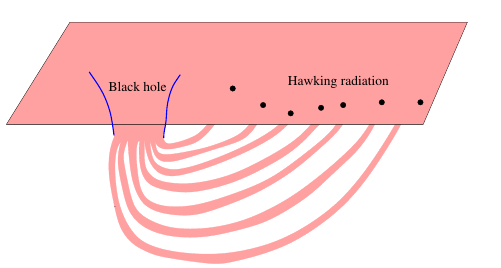
One alternative to fuzzballs is the wormhole proposal. A wormhole connects the emitted Hawking radiation particles back to the black hole. Since the radiation goes very far from the hole, this is a kind of long distance nonlocality.
Resolving the information paradox has led us to the fuzzball paradigm. This paradigm, in turn, provides a deep lesson about quantum gravity.
Traditionally, any theory of quantum gravity was expected to be relevant only over very tiny distances -- distances shorter than the planck length \(l_p\) which is about \( \sim 10^{-33} \, cm\). How then can string theory change the entire interior of a black hole, which is typically several Km across?
The answer is that is that a black hole is characterized by a very large number \(N\) : the number of elementary constituents that make the hole. For a typical stellar hole, we have \(N \sim 10^{40}\). We then need to ask: if a large number \(N\) of elementary constituents are involved in a physical process, then is the length scale relevant for quantum gravity still \( l_p\), or could it change to something like \( N\) times \( l_p\)?
The fuzzball paradigm teaches us that in string theory, the distance over which quantum gravity is relevant indeed grows with \( N\), in such a way that the range of these effects is always comparable to the horizon radius. Thus quantum gravity emerges from the microscopic to the macroscopic domain.
This lesson appeared so radical that at first many people did not accept it, and kept looking for other ways to resolve the information paradox. One suggestion was that the black hole remained as in the third iteration to a good approximation, but tiny quantum gravity effects encoded the information in subtle ways among the large number of particles emitted in Hawking radiation. In fact Hawking himself surrendered a bet to John Preskill in 2004, saying in essence that such tiny corrections might have a cumulative effect that would invalidate his 1975 claim that black holes posed a puzzle. But most people did not agree with Hawking's 2004 reasoning, and Hawking's co-signer on the bet - Kip Thorne - refused to surrender his position that black holes posed a puzzle.
In 2009, the small corrections theorem was proved, which used results from quantum information theory to show that tiny corrections could not encode the information in the emitted radiation. This theorem provided a natural closure for the fuzzball paradigm: the theorem showed that large modifications were needed at the horizon of the black hole used in the third iteration, and the fuzzball structure provided exactly such large modifications. Meanwhile more and more configurations for black holes were constructed, and in each case the structure was found to be that of a fuzzball, rather than of the traditional hole with horizon.
Nevertheless some people continued with efforts to preserve the traditional structure of the black hole while evading the information paradox. These efforts typically involve altering some fundamental principle of quantum theory or gravity. In particular, some of these efforts try to evade the information problem by saying that particles that float far away as Hawking radiation are not distinct from entities that live inside the black hole; this identification of 'data bits' is represented by the wormholes mentioned above.
In our full exposition of the information paradox, we will explain these ideas in detail.