As an instructive exercise in setting up and running cosmological N-body simulations with Gadget2 I ran a 2563 particle Lambda-CDM simulation using an initial conditions file from The Cosmic Data Archive and compared against published results. There are three papers which show results using these initial conditions: Heitmann et al. 2004, Heitmann et al. 2007 , and the Gadget2 code paper. The Heitmann et al. papers are part of an ambitious code comparison project by Katrin Heitmann and Salmann Habib at Los Alamos National Lab (along with others), hence I tend to refer to this project as the "LANL" test, or the Gadget2/LANL IC code comparison project.
The first step was to convert the LANL initial conditions file to Gadget format. Both are binary formats but the Gadget format is considerably more complex than the LANL format (which does not have a header). I used snippets of code from the Gadget source i/o routines to create a C code to do this. Here are those codes: lanl_ic2gadget.c and lanl_out2gadget.c. The lanl_out2gadget.c code may also be useful to convert the final-step LANL-format particle files from other codes also downloadable from the Cosmic Data ArXiv into Gadget format for analysis. In this project I compare the results using the particle file from my own simulation to the results from the Gadget2 particle file available on that site.
The second step was to infer the parameters of the simulation from the papers. The cosmological parameters are read off easily enough. What is more difficult is determining the Gadget2 code parameters (e.g. ErrTolTheta, PartAllocFactor, SofteningHalo, etc.). Here is the parameter file that I used for the large box simulation which has parameters that give satisfactory results when compared to those papers and the Gadget2 final output particle file which is downloadable from the Cosmic Data ArXiv website. I also set DPMGRID=384 in the Gadget2 makefile so that the PM part of the Gadget2 simulation uses a 3843 mesh to calculate the forces on the 2563 particles.
The results I show here are only for the large box (L = 256 Mpc/h = 360 Mpc on a side) simulation. I could have also done the smaller box (L = 64 Mpc/h = 90 Mpc on a side) simulation but since it is more computationally expensive to do a small box simulation with 2563 particles than a large box simulation with 2563 particles (see Table 1 in the Gadget2 code paper) I opted to only try to reproduce the results of larger box simulation to meet my objective of making sure things are working properly. The simulation used here took 15 hours on eight 1.3 GHz Itanium2 processors distributed across four nodes on the Itanium cluster at OSC.
Note that I am not 100% sure that may parameter file uses exactly the same parameters as the Gadget2 runs that are described in these papers. Nevertheless the agreement between my output with the LANL output for the various tests I've looked at leads me to believe that the parameter file above is pretty close to the values that Volker Springel used in his run and that my implementation of the Gadget2 code on the machines at OSC are working properly.
Feel free to contact me at orban.14@osu.edu if you have questions about the codes or the results.
-Chris Orban (OSU)
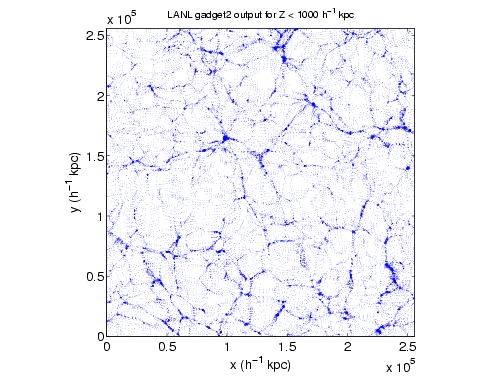
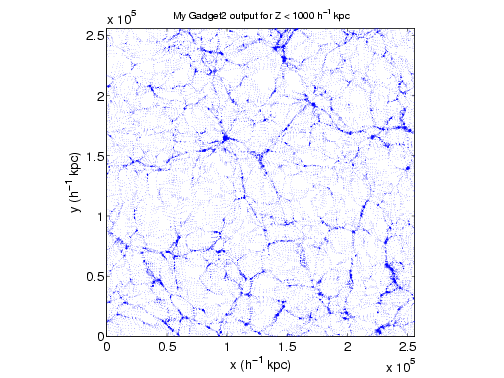
Here are slices of the volume at z = 0 from my simulation compared to the same slice from the LANL particle file. Looks good!


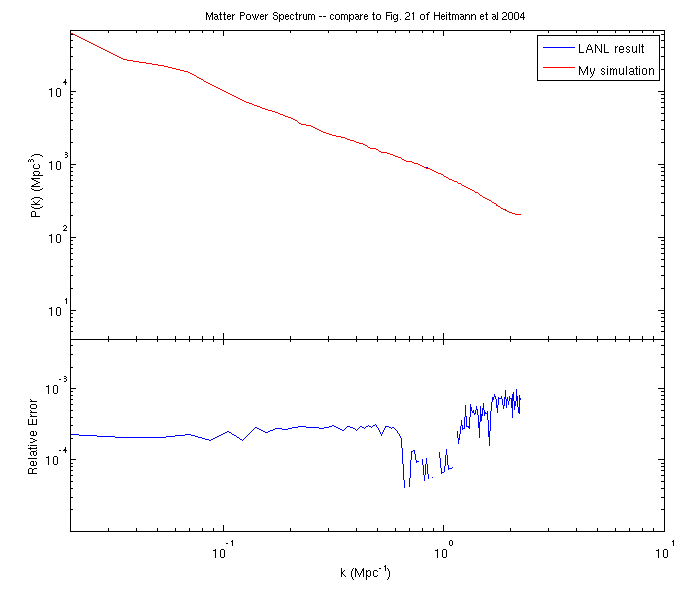
Here's the results for the matter power spectrum at z = 0. The curves from the LANL output (blue) and my output (red) are on top of each other.
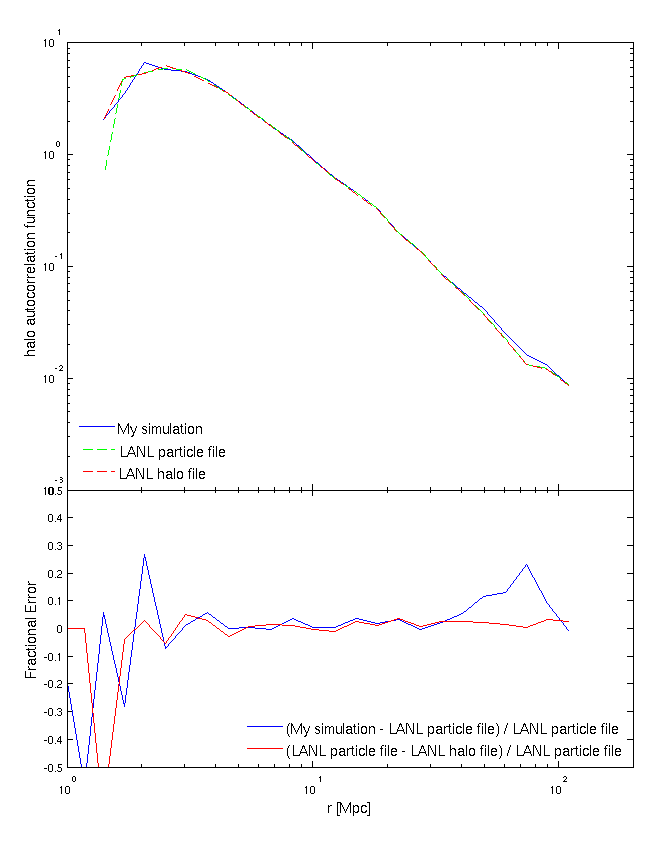
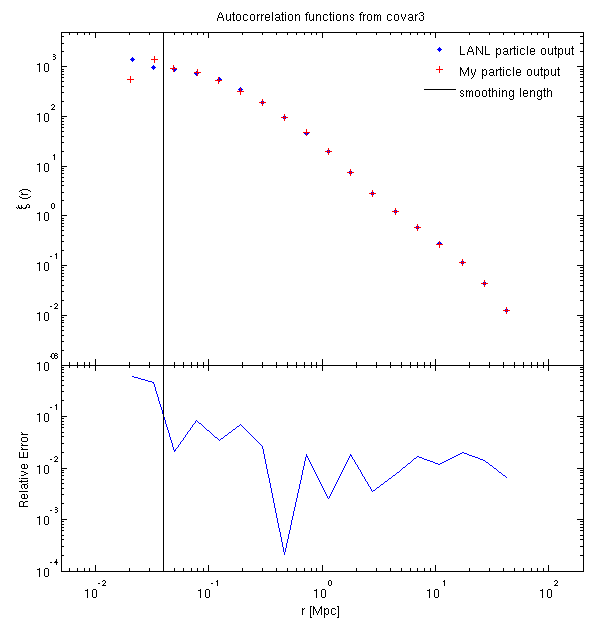
Here is the autocorrelation function at z = 0.
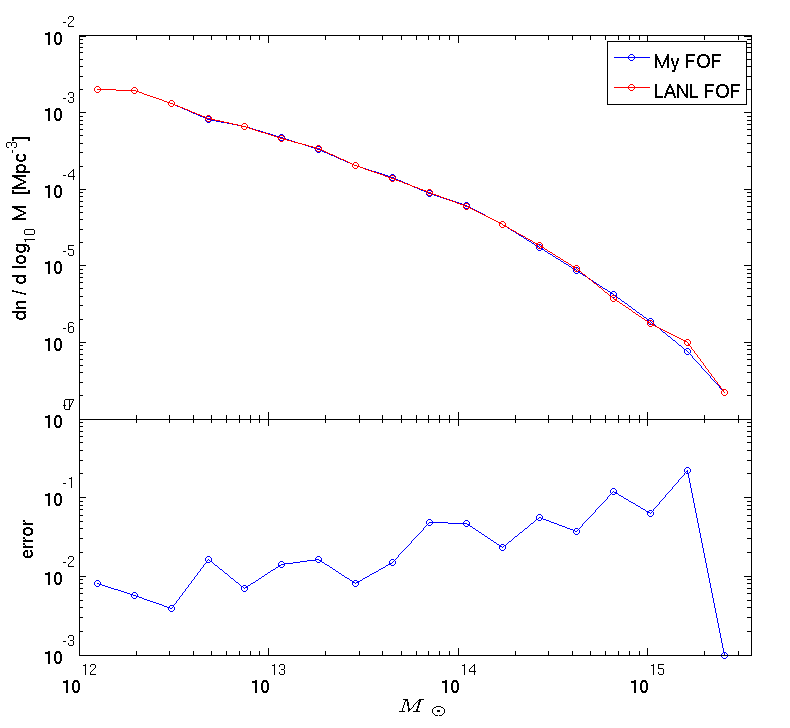
Here is the halo mass function at z = 0.
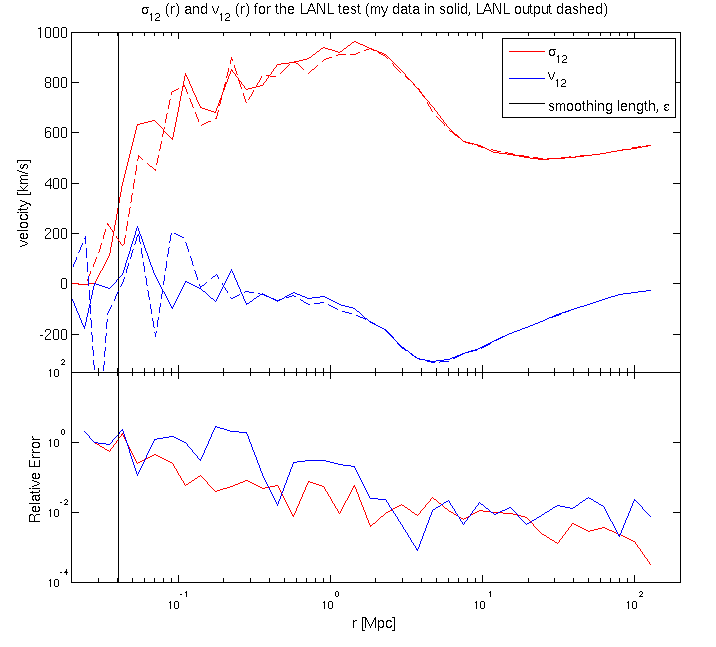
Here is the mean pairwise velocity (blue) and the velocity dispersion (red). My output is in solid lines, the LANL particle distribution results are in dashes.
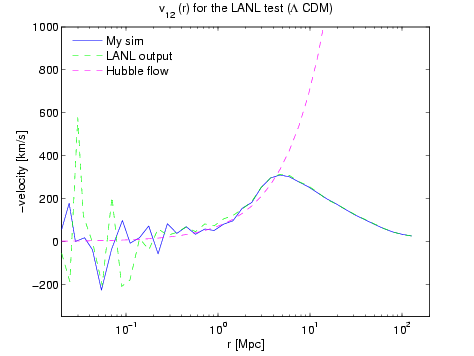
Here's a plot of just the mean parwise velocity (times -1) with the analytic "Hubble flow" result overplotted. Physically this analytic function is more accurately the effect of the coordinate system expanding and the particles at close distances having a mean physical velocity of zero. In any case the analytic result has no free parameters and it matches well.
Here's a plot of the halo autocorrelation function at z = 0.