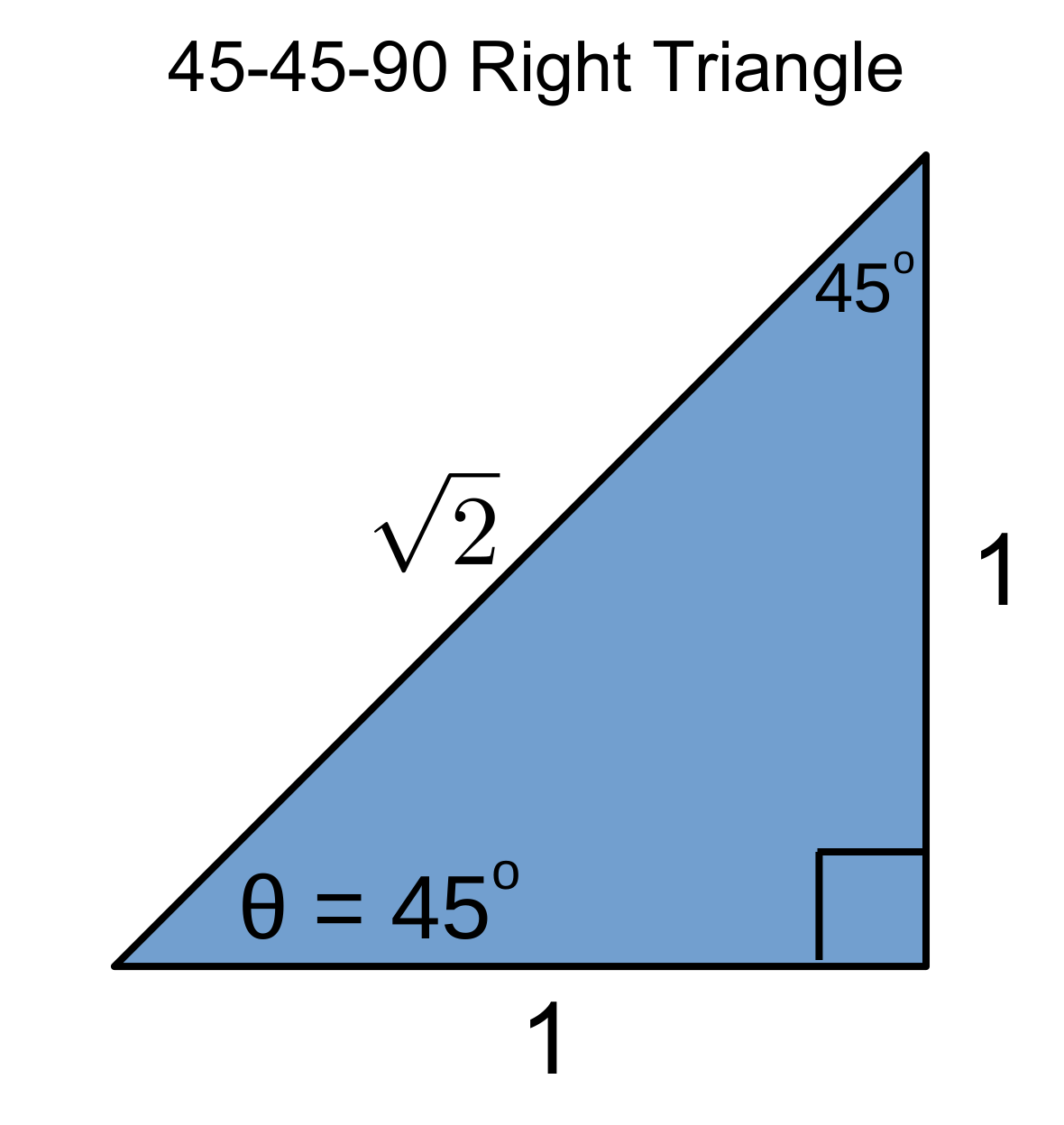
If you completed the Pi day activity and were surprised at how long it took to calculate the digits of $\pi$ there is good news! There is a better way to calculate the digits of Pi! It starts by thinking about a 45-45-90 right triangle:

Step 1. Convert 45 degrees to radians
I know what you're thinking: How does does $\pi$ relate to 45-45-90 triangle? It starts by converting 45 degrees into a fraction of $\pi$.
Remember that there are 2 $\pi$ radians in a circle (360 degrees). This being the case we can convert 45 degrees to radians like this: $$ \theta = 2 \pi \cdot \frac{\theta_{\rm deg}}{360} $$
What do you get for $\theta$ as a fraction of $\pi$? In other words, if $\theta = \pi / N$ then what is $N$?
Step 2. Trigonometry
Hopefully you remember SOHCAHTOA. Let's think about the TOA, in other words: $$ \tan \left( \theta \right) = \frac{{ \rm opposite}}{{ \rm adjacent}} $$
For the 45-45-90 triangle this becomes: $$ \tan \left( \theta \right) = \frac{1}{1} = 1 $$
This means that we can do $\tan^{-1}$ to both sides of the equation to get the angle $\theta$ like this: $$ \tan^{-1} ( \tan( \theta)) = \tan^{-1} (1) $$ $$ \theta = \tan^{-1} (1) $$
Note #1: Another way of writing the equation above is like this: $$ \theta = \arctan(1) $$
In other words, $\arctan$ and $\tan^{-1}$ are different names for the same thing.
Note #2: People refer to $\tan^{-1}$ as "inverse tangent" and they refer to arctan as "arctangent". But of course they are talking about the same thing. In code it is easier to write arctan than tan^-1 so for this activity we will just use arctan because computers are cool too.
Step 3. Putting it all together
Putting everything together so far means that the following is true: $$ \theta = \arctan(1) = \frac{\pi }{4} $$
So if we can just estimate $\arctan(1)$ we can multiply that by 4 to get $\pi$ like this: $$ \pi = 4 \cdot \arctan(1) $$
Optional: Go to Desmos or some other scientific calculator and calculate $\arctan(1)$ and then multiply by 4. Does the number look familiar? This is a totally valid method of calculating $\pi$ but how do we calculate arctan(1)?
Step 4. Calculate arctan(1)
Great! How do we estimate $\arctan$ ? By using a power series like this: $$ \arctan (q) = q - \frac{{{q^3}}}{3} + \frac{{{q^5}}}{5} - \frac{{{q^7}}}{7} + \frac{{{q^9}}}{9} - \frac{{{q^{11}}}}{{11}} + ... $$
where $$q = \frac{\rm opposite} {\rm adjacent} $$
Exactly where this power series comes from and how every function can be reduced to an approximate power series over some range using a "taylor series" is not something that we need to worry about today.
For our 45-45-90 triangle $ q = 1/1 = 1 $. Simple! Here is what the power series looks like now: $$ \arctan (1) = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{{11}} + ... $$
This is sometimes referred to as the Leibniz formula for pi
Let's put this in a code and see what we get!
Step 5. Open a computer code that is using the first 2 terms of the arctan series to estimate $\pi$ .
Click here to open a simple code in an editor!
Press the play button in the top left to run a code that calculates the first two terms in the series and see what happens.
Step 6. Look at the code
Here is the code you will find there:
arc_tan = 0;
function draw() {
background(240); // background is light gray
drawText("Estimating Pi Using ArcTan", 0.2*width, 0.95*height);
arc_tan = 1 - 1/3;
drawText("Est. Pi =", 0.01*width, 0.85*height);
drawText(4*arc_tan,0.45*width,0.85*height);
drawText("True Pi =", 0.01*width, 0.8*height);
drawText(PI,0.45*width,0.8*height);
drawText("Est. - True =", 0.01*width, 0.75*height);
drawText(4*arc_tan - PI, 0.45*width, 0.75*height);
error = abs(4*arc_tan - PI);
drawText("abs(Est. - True) =", 0.01*width, 0.75*height);
drawText(error, 0.45*width, 0.75*height);
noLoop(); // Only run draw() once and then end the program
} // end draw() DO NOT ADD ANYTHING PAST THIS LINE!!!
Normally this code runs over and over again, many times per second. But because we are using noLoop(); it will run just once and end the program. If you completed any of the "physics of video games" activities you may remember that noLoop(); was used whenever we added a game over to the code. We are using the same function here.
Step 7. This is not a great way to estimate Pi
If you run the program it will estimate $\pi$ to be 2.6667 because it estimates $\arctan(1)$ to be $1 - 1/3 = 2/3$ and then multiplying by 4 gives 8/3 = 2.6667 which is not so very close to 3.14.... We didn't really need a code to do this calculation but later it will be helpful to use a code.
Let's improve on this by adding more of the terms in the series!
Step 8. Use the First 5 Terms in the ArcTan Series to Calculate the digits of Pi
Modify the code to estimate $\pi$ with the first 5 terms in the arctan series.
Change this:
arc_tan = 1 - 1/3;
to this:
arc_tan = 1 - 1/3 + 1/5 - 1/7 + 1/9;
Does this do a better job of estimating pi? Is abs(Est. - True) closer to zero? How does this compare to using only the first two terms?
Step 9. Use the First 10 Terms in the ArcTan Series to Calculate the Digits of Pi
Let's estimate Pi with the first 10 terms in the arctan series.
Change this:
arc_tan = 1 - 1/3 + 1/5 - 1/7 + 1/9;
to this:
arc_tan = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 - 1/15 + 1/17 - 1/19;
Is our estimate with 10 terms closer to the true Pi, than with 2 or 5 terms?
Step 10. Now include n terms!
Let's modify the code so that as time goes one we are using more and more terms to estimate $\pi$. Hopefully this will get closer and closer to the true value of 3.141592654....
Step 10a. Remove noLoop();
We need the draw function to run over and over again like it does normally. Remove noLoop(); from the end of the program.
When you run the code now it will probably look the same as before, but really the draw() function is running many times per second.
Step 10b. Add n = 0; at the top of the program
We are going to use n as the number of terms. Initially n should be zero so at the very beginning of the program and right below arc_tan = 0; set n = 0;
arc_tan = 0; n = 0;Go ahead and add this at the very beginning of the code
Step 10c. Add n = n + 1; inside the draw function
Each time the draw function runs we need to increase n to keep track of how many times it has been run.
Add this code to the middle of draw()
n += 1;
drawText('n = ',0.01*width,0.7*height);
drawText(n,0.1*width,0.7*height);
If you copy this into your code it will won't do much besides count the number of times that draw() has been run.
At this stage your code should behave like this
Step 10d. Look at the pattern
Here is the series up to 10 terms $$ \arctan (1) = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \frac{1}{13} - \frac{1}{15} + \frac{1}{17} - \frac{1}{19} + ... $$
Do you see the pattern? Can you write down what the pattern is?
Step 10e. Add arc_tan += ????
Now it is time to replace arc_tan = 1 - 1/3 + 1/5 - ... with this:
arc_tan += ????
The main thing to notice is that we have replaced = with += . So each time we run the draw function we will add something to arc_tan. The first time (n = 0) we should add 1, the second time (n = 1) we should add -1/3, the third time (n = 2) we should add 1/5 and so on.
Here is a table if it helps:
| n | Denominator |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| ... | ... |
Advice/Hints:
There is more than one way to write this code, especially because there is more than one way to switch between adding and subtracting the fraction.
You may have noticed that if n is even then we add the fraction but if n is odd then we subtract. Here is some code that figures out if n is even or odd:
if (n/2 === ceil(n/2)) { // n is even
arc_tan += ????;
} else { // n is odd
arc_tan -= ????;
}
Please notice that the second expression for arc_tan uses -= instead of += so that we are subtracting the value of whatever comes next!
Another way to make sure we switch back and forth between + and - is to add a variable equal to 1 and then multiply that variable by -1 each time.
Working code
There are many different ways to add up the series, so feel free to modify the code in a way that makes sense to you.
As long as your estimate for pi gets closer and closer to the true value like it does at this link, your approach is correct! That's the nice part about solving math problems with computers. As long as you can test your code and show that it's working then it's right!
Optional: Add a fun graph
If you want to watch the estimate for Pi get closer to the true value you can add this to your code:
graph1.addPoint(4*arc_tan); graph1.display(); graph2.addPoint(PI); graph2.display();
When you add this to the code your program should behave like this
1. We thought about 45-45-90 trangles and arctan(1) to calculate the digits of $\pi$. How would you use a 30-60-90 triangle to calculate the digits of $\pi$ using arctan?
Advice #1: Use the general formula for arctan $$ \arctan (q) = q - \frac{{{q^3}}}{3} + \frac{{{q^5}}}{5} - \frac{{{q^7}}}{7} + \frac{{{q^9}}}{9} - \frac{{{q^{11}}}}{{11}} + ... $$
Advice #2: Instead use pow(q,n) instead of q^n (which won't work)
2. With a 30-60-90 triangle how would you use arcsin or arccos to estimate the digits of pi?
One criticism of using arctan to calculate the digits of pi with a 30-60-90 triangle is that you have to calculate the square root of 3 before you can use that arctan expansion and how do you know that you have calculated $\sqrt{3}$ correctly? Probably you've calculated $\sqrt{3}$ just fine but, you know, people talk, seeds of doubt, etc.
Hopothetically, how would you use arcsin or arccos to calculate the digits of pi with a 30-60-90 right triangle? Can you do this without using a $\sqrt{}$ function?
Here is the series expansion for arcsin: $$ \arcsin(q) = q+ \frac{1}{2}\frac{q^3}{3} + \frac{1 \cdot 3}{2 \cdot 4}\frac{q^5}{5} + \frac{1\cdot 3\cdot 5}{2 \cdot 4 \cdot 6}\frac{q^7}{7} + ... $$
Unfortunately the series expansion for arccos includes a factor of $\pi$ in it so it's kind of cheating to use it to estimate $\pi$. The workaround is to remember that $\sin(90 - \theta) = \cos \theta $ so if you really want to calculate $\cos(30)$ or $\cos(60)$ you can calculate $\sin(60)$ or $\sin(30)$ instead, in which case you can use the above formula.
If this seems like a lot of work for a number we already know, consider the possibility that we are the first people to calculate the digits of pi and you are trying to figure out a way of double checking the answer you got with arctan.
3. Compare this approach to Pi Day Part 1
Think about Pi Day Part 1 where we used a random number generator and our geometry skills to calculate the digits of Pi. Is using arctan(1) a "better" method (more accurate more quickly) than this approach? Explain your reasoning.
Feeling ambitous? Check out this wikipedia page on approximating pi Can you modify the program to calculate the digits of $\pi$ using one of these methods?