You are trapped on a deserted island by a psychopath who is keeping you there until you can determine the digits of $\pi$ out to many decimal places. All you have is the p5.js web editor! What to do!? (FYI: Try not to think about giving up and just enjoying the island.)
Step 0. Think about how we're going to do this!
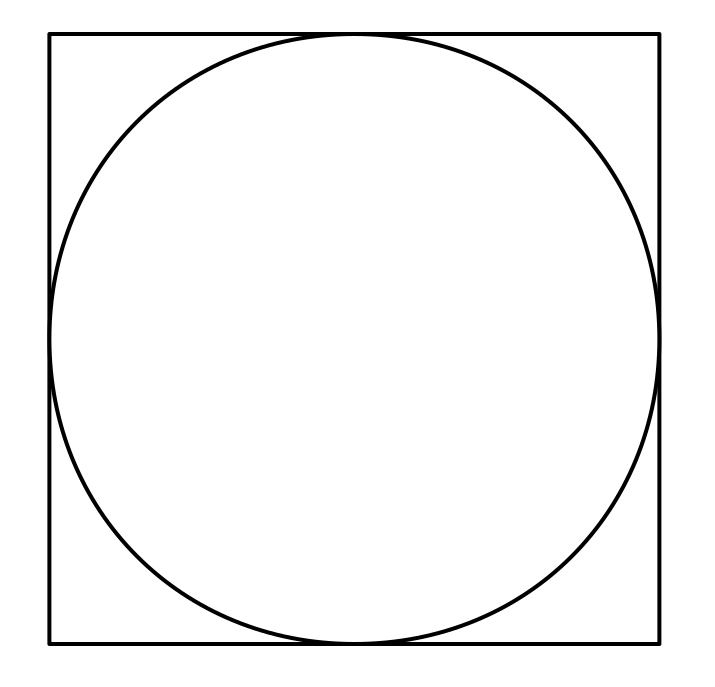
There are a couple different ways of estimating $\pi$. A simple one is to randomly throw darts at a dart board that looks like this:

If you count up the darts that fall within the circle and compare to the total number of darts thrown, the ratio should be equal to the area of the circle divided by the area of the square. From the figure, it's clear that the length of the square ($L$) is twice the radius of the circle ($R$). Therefore the following is true: $$\frac{A_{\rm circ}}{A_{\rm sq}} = \frac{\pi R^2 }{L^2} = \frac{\pi R^2 }{(2 R)^2} = \frac{\pi R^2 }{4 R^2} = \frac{\pi}{4} $$
So if we randomly throw the darts, the ratio should come out to $\pi/4$. Therefore we can just multiply the ratio by 4 to get an estimate for $\pi$.
If this seems ridiculous, the alternative is to create a super-large circle and get a super precise ruler and measure the circumference as best you can.
Step 1. Write a program that draws random points in a square!
Click here to open a simple code in an editor!
Modify this code to draw points at random locations.
Change this:
x = 0.5*radius; y = 0.5*radius;
to this:
x = random(-radius,radius); y = random(-radius,radius);
After you make this change your code should act like this
Step 2. Figure out which points are in the circle
Let's add an if statement to the program so that points inside the circle are gray and points outside it are black.
First, delete the reference to drawPoint(x,y,color1);
Now copy the code below and change the "something" and "something else" to some formula that will detect if the random point (x,y) is within the circle:
if ( something < something else) {
drawPoint(x,y,color2);
} else {
drawPoint(x,y,color1);
}
Advice: To make things easier the code defines the center of the circle is at x = 0, y = 0. That makes the formula for the distance between the point (x,y) and the origin rather simple.
If you do this right your code should behave like this
Step 3. Add a counter for the total number of points
Keep track of the total number of points drawn by adding this code to the draw function:
Npoints += 1.0;
Add this towards the end of the draw function. This will increase Npoints by one every time the draw function is run.
Step 4. Add a counter for the points that fall inside the circle
Put this code in the right place so that it increases Npoints_incirc by one every time a point falls within the circle.
Npoints_incirc += 1.0;
Step 5. Write the ratio of the points x4 to the console
The ratio of the number of points in the circle (Npoints_incirc) to the total number of points (Npoints) should equal $\pi/4$. Therefore if we just multiply this ratio by 4 we should get an estimate for $\pi$.
Copy this into your code towards the end of the draw() function:
print(4.0*Npoints_incirc/Npoints);
Step 6. See how long it takes to determine $\pi$ to many digits
How long does it take to calculate $\pi$ to three digits? four digits? Notice that the estimate for $\pi$ isn't very accurate until the dots pretty clearly show a circle on top of a square.
If you are curious to write the difference between your answer and the true value of $\pi$ to the console you can add this to your code:
print(abs(PI-4.0*Npoints_incirc/Npoints));
Finished!
Next steps:
If this seems like a slow way to determine the digits of $\pi$, it turns out there is another way but it involves some trig. Go to the next exercise to see how! (still in progress)