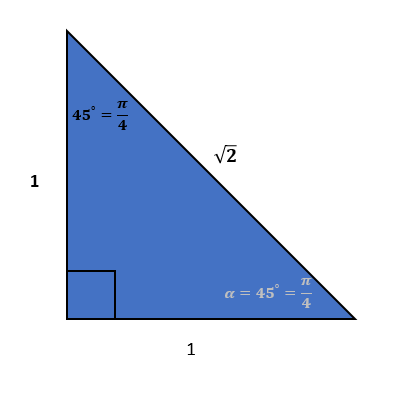
While being trapped on a deserted island by a psychopath, you wonder if there is a more efficient method to calculate $\pi$ . You previously calculated $\pi$ using the dart board method. While thinking about your Trigonometry course taken at Taylor High School, you recall that the 45-45-90 special right triangle.
SOHCAHTOA is unforgetable and you decide to find
\[\tan \left( \alpha \right) = \frac{{opposite}}{{adjacent}}\] You calculate: \[\tan \left( \alpha \right) = \frac{1}{1} = 1\] So this means that, \[\arctan (1) = \frac{\pi }{4}\] With some basic algebraic manipulation, you can see that \[\pi = 4 \cdot \arctan \left( 1 \right)\] You decide to test this method and compare to the previous dart board method.Step 0. Recalling Some Trigonometry Knowledge
ArcTan(t) can be written as the following series:
\[\arctan (t) = t - \frac{{{t^3}}}{3} + \frac{{{t^5}}}{5} - \frac{{{t^7}}}{7} + \frac{{{t^9}}}{9} - \frac{{{t^{11}}}}{{11}} + ...\] So, \[\arctan (1) = 1 - \frac{{{1^3}}}{3} + \frac{{{1^5}}}{5} - \frac{{{1^7}}}{7} + \frac{{{1^9}}}{9} - \frac{{{1^{11}}}}{{11}} + ...\] Which gives, \[\arctan (1) = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{{11}} + ...\]Step 1. Look at a computer code that is using the first 2 terms of the arctan series to estimate $\pi$ .
Click on the link below and click the 
symbol. This will approximate $\pi$ using the first 2 terms in the arctan series.
Click here to open a simple code in an editor! Notice the 9th line of code: arc_tan = t - pow(t,3)/3 The pow function allows you to use exponents. The first entry is the base and the second is the exponent (pow(base, exponent)). Below is a clip from p5js.org.
Step 2. Use the First 5 Terms in the ArcTan Series to Estimate Pi
Modify this code to estimate $\pi$ with the first 5 terms in the arctan series.
Change this:
arc_tan = t - pow(t,3)/3
to this:
arc_tan = t - pow(t,3)/3 + pow(t,5)/5 - pow(t,7)/7 + pow(t,9)/9
Notice that once you push , a white preview shows up. The last line in the white preview is "abs(Est. - True). This is finding the absolute value of the error or our estimated Pi value minus the true value of Pi. Is our estimate with 5 terms closer to the true Pi, than with 2 terms?
If you do this right your code should behave like this
Step 3. Use the First 10 Terms in the ArcTan Series to Estimate Pi
Modify this code to estimate Pi with the first 10 terms in the arctan series.
Change this:
arc_tan = t - pow(t,3)/3 + pow(t,5)/5 - pow(t,7)/7 + pow(t,9)/9
to this:
arc_tan = t - pow(t,3)/3 + pow(t,5)/5 - pow(t,7)/7 + pow(t,9)/9 - pow(t,11)/11 + pow(t,13)/13 - pow(t,15)/15 + pow(t,17)/17 - pow(t,19)/19
Is our estimate with 10 terms closer to the true Pi, than with 2 or 5 terms?
Step 4. Look at Code That Loops!
Click here to open the code that loops (doesn't stop). You'll learn more about looping below.
You should notice that we keep getting closer to Pi as we increase our number of terms. In otherwords, the error (abs(Est. - True) is getting smaller. Now let's look at some code that never stops and keeps adding more and more terms. Notice that after you hit , there is now a 4th line in the preview that tells us how many terms has been ran in our code.
You should see this in the preview window.
Pay attention how the error keeps getting smaller and the Est. Pi is getting closer to the True Pi as the # of Terms increases.
Step 5. Increase the framerate
Looking at the 3rd line of code from the last step, you should see this:
framerate = 10;
Now change this line to this:
framerate = 60;
If you do this right your code should behave like this
The code from Step 4 was at a speed of 10 frames per second. The maximium and default speed is 60 frames per second. The speed was reduced to make it easier to read the values calculated. Now that the code is at 60 frames per second, it is at the same speed of the previous activity with a Dart Board. Which method will estimate Pi faster?
1. Why do you feel that we used arctan(1) to estimate $\pi$ ? Why not use a 30-60-90 triangle or another right triangle? Think about how f(x) = arctan(x) function behaves and look at some special right triangles (45-45-90, 30-60-90, etc.)
2.Can you express arctan(t) using sigma notation?
The following is how you write arcsin(t) and arccos(t) in sigma notation. These formulae are valid for \[ - 1 \le t \le 1\]
\[\begin{array}{l} \arcsin \left( t \right) = t + \frac{1}{2}\left( {\frac{{{t^3}}}{3}} \right) + \frac{{1 \cdot 3}}{{2 \cdot 4}}\left( {\frac{{{t^5}}}{5}} \right) + \frac{{1 \cdot 3 \cdot 5}}{{2 \cdot 4 \cdot 6}}\left( {\frac{{{t^7}}}{7}} \right) + ... = \sum\limits_{n = 0}^\infty {\frac{{\left( {2n} \right)!}}{{{2^{2n}}{{\left( {n!} \right)}^2}\left( {2n + 1} \right)}}{t^{2n + 1}}} \\ \arccos (t) = \frac{\pi }{2} - \left( {t + \frac{1}{2}\left( {\frac{{{t^3}}}{3}} \right) + \frac{{1 \cdot 3}}{{2 \cdot 4}}\left( {\frac{{{t^5}}}{5}} \right) + ...} \right) = \frac{\pi }{2} - \sum\limits_{n = 0}^\infty {\frac{{\left( {2n} \right)!}}{{{2^{2n}}{{\left( {n!} \right)}^2}\left( {2n + 1} \right)}}{t^{2n + 1}}} \end{array}\]Look over the code from the link provided in step 4. Can you identify where the sigma notation from challenge question #3 is located in the coding window? Watch the short video below to help you understand what a loop is.
3. Use the expansion for arccos in question 2 to calculate the digits of $\pi$ (Hint: Use a 30-60-90 triangle). Is using arccos better (more accurate more quickly) than using arctan? Or is it about the same? Is it worse?
4. Think about the "dart board" method that was discussed in an earlier coding activity. Is using arctan(1) a "better" method (more accurate more quickly) than the dart board method? Explain your reasoning.