Step 5. Let's get tricky
Let's make a change to the if statement so the win fraction is something other than 50%.
For example, change diceval1 > 3 to something else like diceval1 < 2 or diceval1 > 4.
Or perhaps change the if statement so that the dice value is equal to some number (example: diceval1 == 6). Sometimes in a board game you get in situations where you have to roll a 6 or a 1 or something else in order to win.
Make this change, then do a calculation to figure out what the true win fraction should be! Then modify the graph2.addPoint(50) line of code so that it draws a line at the correct probability for whatever you modified the if statement to do.
Answers will vary, but the result might look something like this.
Do not just change the number for the horizontal line until it looks right! Think about the answer that you should get!
Step 6. The game of Risk, finally
The simplest scenario in the game of risk is when one player attacks another player and each player only has one army. According to the rules, the attacking player gets one dice and the defending player gets one dice. Whoever rolls the highest value will win the battle. If there is a tie, then the defender wins the battle.
Step 6a. Add a second dice to the program
Our program only has one dice. Go ahead and add another dice with this code:
diceval2 = rollDie(); // random integers between 1 and 6
print(diceval2);
drawText('Dice2 value = ' + diceval2,0.55*width,0.9*height);
Let's think of diceval1 as the attacking dice, and diceval2 as the defending dice.
Step 6b. Modify the if statement
Now modify the if statement so that if diceval1 is larger than diceval2 then it will be a "win", but if diceval1 is less than diceval2 or if they are equal it will not be a win.
Your code should behave like this if modify the if statement correctly
It would be nice to add a horizontal line to the screen so we can see how long it takes to produce the "true" probability. We could do this by trial and error, but instead lets think about the combinations.
Step 6c. Think about the combinations
When you roll two, six-sided dice there will be $6^2 = 36$ combinations. Unless the dice are weighted (in other words if someone is cheating) all 36 combinations are equally likely to occur. The question is how many of these combinations result in the attacking dice winning.
Note: Remember that if the dice are the same value then the defender wins!
Fill in this table for whether the attacker or defender wins. Write A if the attacker wins and D if the defender wins
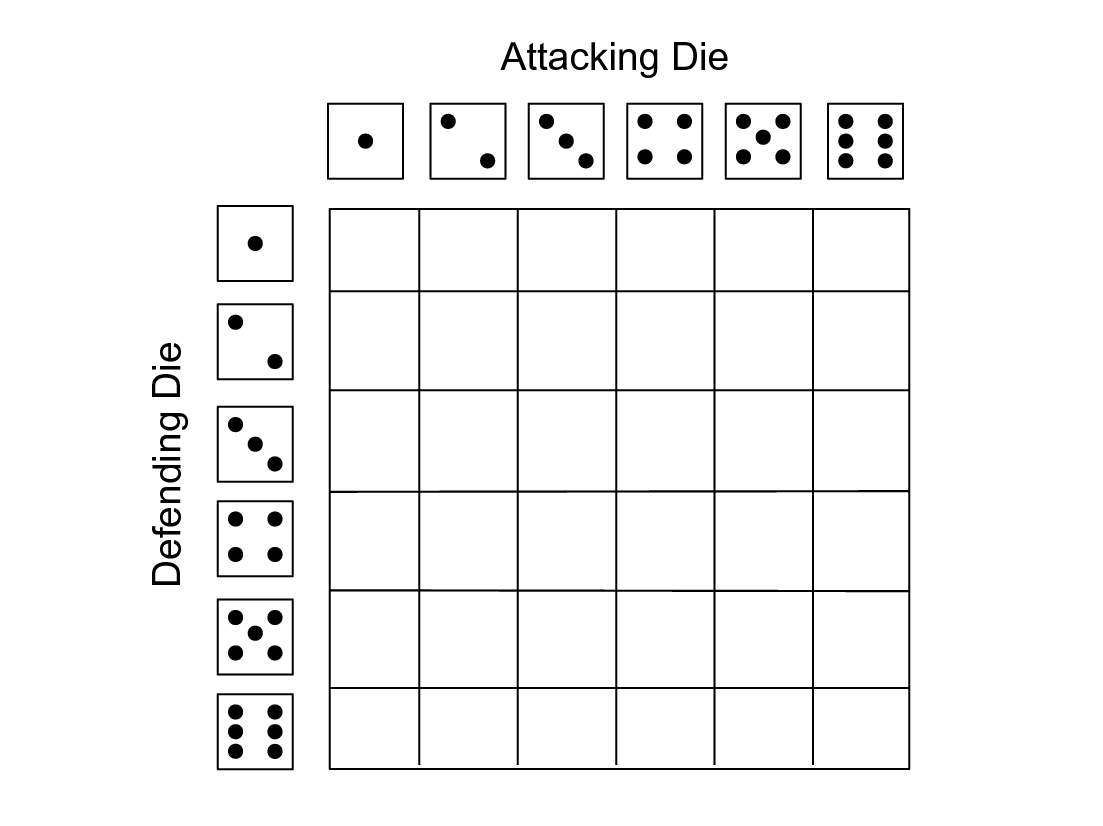
Of the 36 combinations how many of these would the attacking die wien?
Step 6d. Show this probability in the code
Take the number of combinations where the attacker wins and divide it by 36 to get the win fraction. Then multiply by 100 to get the percentage. Then modify this line of code:
graph2.addPoint(50); graph2.display();
So that instead of showing the 50% probability as a horizontal line it shows whatever percentage you just determined.
If you make this change your code should behave like this
Step 7. Should you attack?
Based on what you found, would you go ahead with the 1 dice versus 1 dice attack? Why?
Step 8. Two dice vs. one dice
You can increase your probability of winning by attacking the one die (one army) with two dice instead of one. If the defending dice is greater than or equal to the larger of the two attacking dice, then the defender wins. But if the defending dice is less than the larger of the two attacking dice, then it is a win for the attacker.
Note: In the real game, you can do two dice versus one dice, lose the first round and then do 1v1 and potentially win. Here we will just consider this first round. In the real game, if you lose the first round of 2 vs 1, you will probably be reluctant to do 1 vs 1 because the probability of winning is less than 50%.
Modify your code so that there are two attacking dice and one defending dice. This will involve adding another line with the function rollDie();. This function (rollDie()) should now appear three times in the program because there are a total three dice being thrown.
Advice #1: The function max(val1,val2) will return the larger of the two values. Use this to find the value
Advice #2: Set the horizontal line back to 50%. We want to know if two dice vs one dice is more than 50% likely to win.
If you do this correctly your code might behave like this
In this link we have re-labeled dice 1 and dice 2 as attacking die and dice 3 is the defending dice.
Optional Challenge: Step 9. Think about the combinations!
With three dice there are now $6^3 = 216$ combinations. How many of these have the attacking die winning? What does the win percentage work out to?
Step 10. Three dice vs. one dice
Modify the code so that there are three attacking dice and one defending dice. What is the probability of winning now?
Advice: With four dice involved this becomes nearly impossible to map out by hand, but if you want you can look at this nerdy write up about the probabilities in Risk to double check your answer.
Step 11. Reflection
Now that you know the probability of winning an attack with one two and three dice versus one dice defending, do you have any thoughts on how you might play the game differently? Attack less? Attack more? Use more dice to attack? Less dice? Is the 3rd dice worth it? In a complex game like this there are no definitively right answers to this question but think about what you've learned might affect the way you play the game.