Maybe it's valentines day. Maybe it's finally spring! Maybe you are a terrible gardener and incapable of growing flowers. Let's make our own flowers using mathematical functions.
Step 0. Take the plunge into polar coordinates!
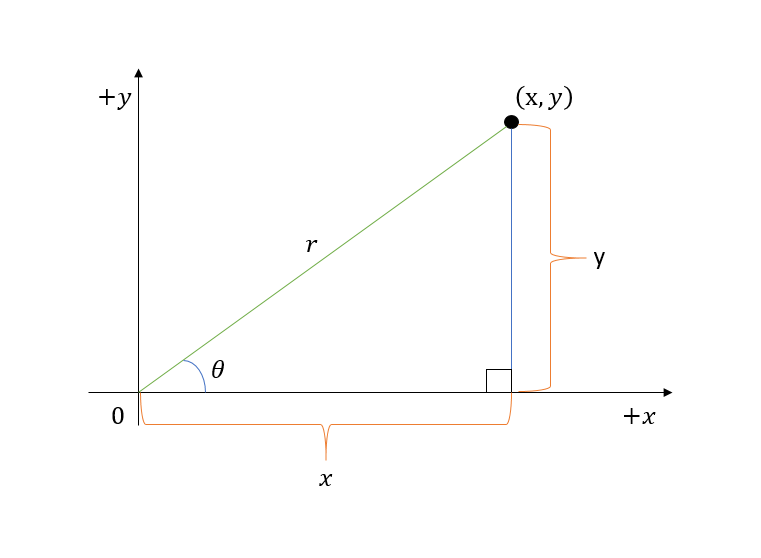
Maybe at some point you've already learned about polar coordinates. If not, that's ok, we'll give you a brief overview. The basic idea is that for every point ($x$,$y$) there is a distance $r$ to the origin, and an angle $\theta$ from the $x$ axis. Let's think about the relationship between $x$ and $y$ and $r$ and $\theta$.

Step 1. Think about how to draw something interesting with polar coordinates
One way to draw interesting things is to make the radius depend on the angle. Here is an example: $$r(\theta) = r_{\rm max} \cdot \cos \left( \frac{n}{d} \cdot \theta \right) $$ $$x(\theta) = r(\theta) \cdot \cos (\theta) $$ $$y(\theta) = r(\theta) \cdot \sin (\theta) $$ Where $n$ and $d$ are constant integers and $\theta$ is our angle in radians!. We will start with $\theta = 0$ and then increase by 0.001 at each iteration.
Step 2. See how this looks in a code
Here is how these equations look in our code:
function draw() {
r = rmax * cos(n/d * theta);
x = r * cos(theta);
y = r * sin(theta);
drawPoint(x, y, flower_color);
theta += 0.001;
}
The program is going to run the draw() function 60 times per second. Each time will increase the value of theta by 0.001. If you are confused by the += sign this video may help
It is tempting to assume that the draw() function is only run once. If you find it hard to believe that the draw() function is being run 60 times per second, this video may help convince you that it is being run multiple times
Step 3. Check out the cool patterns you can make
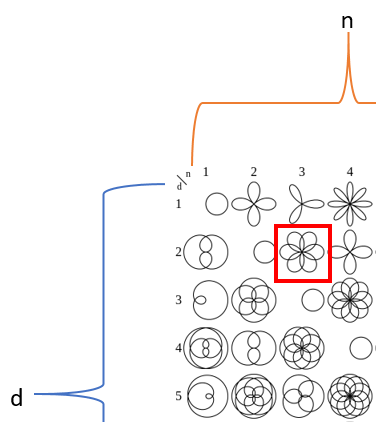
Here are some examples of mathematical flowers for various $n$ and $d$ values. As you can see, some of them look like roses while others look a lot like daisies.
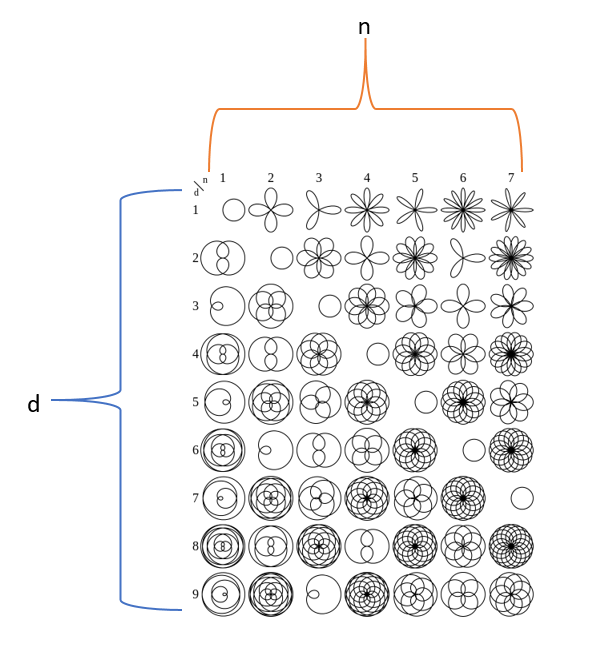
Step 4. Let's Try to Replicate Some Mathematical Flowers from the Table!
Click here to open a simple code in an editor!
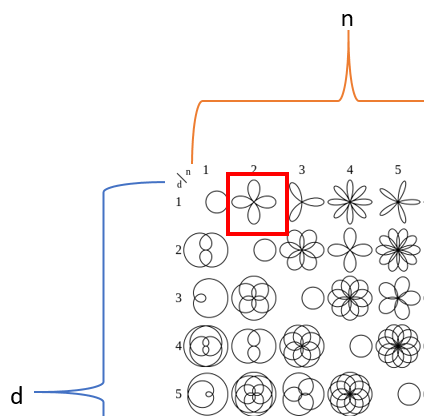
Step 4a. Try out n = 2, d = 1
First let's make this mathematical flower (n = 2, d = 1)
Change this:
n = 1; d = 1;
to this:
n = 2; d = 1;
After you make this change your code should act like this
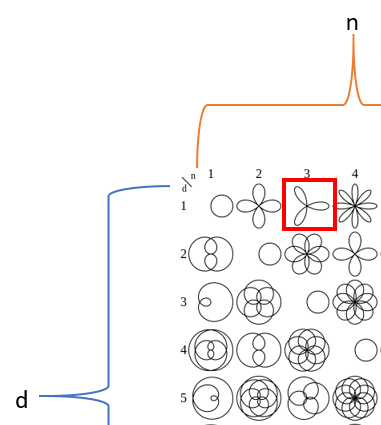
Step 4b. Try out n = 3, d = 1
Next let's make this mathematical flower (n = 3, d = 1)
Change this:
n = 2; d = 1;
to this:
n = 3; d = 1;
After you make this change your code should act like this
Step 4c. Try out n = 3, d = 2
Now let's make this mathematical flower (n = 3, d = 2)
Change this:
n = 3; d = 1;
to this:
n = 3; d = 2;
After you make this change your code should act like this
Step 5. Have Fun Making Your Own Mathematical Flower!
Now it is your turn to make your own Mathematical Flower. Notice in step 4, we varied n and d. We looked at when n / d was an even integer, odd integer, and Half-integer.
Come up with your own values of n and d. Be sure to try a couple of examples where the ratio of n/d is odd number, even number, and half-integer (examples: 1/2, 3/2, 5/2 ...). Make sure to explore n > 7 and d > 9 which were not included on the chart we showed earlier. What patterns do you see with the ratio of n/d?
Step 6. Hurry it up!
It can take some patience to watch the pattern develop. To speed it up, modify the code so that theta increases by 0.01 each iteration instead of 0.005.
Change this:
theta += 0.005;
to this:
theta += 0.01;
After you make this change your code should act like this
Step 7. Have some fun by changing the background and mathematical flower colors
Toward the top of the code, you probably noticed this code:
background_color = [0,0,0]; // black flower_color = [170,170,170]; // gray
The three values shown are RGB color codes. The first number is for the amount of red, the second number is for the amount of green and the third number is for the amount of blue. The max is 255 and the min is 0. In this way, essentially all the colors (purple, yellow, orange, aqua, etc.) can be represented with RGB color codes. (This video explains more about the RGB color codes.)
Change the black (r = 0, g = 0, b = 0) and grey (r = 170, g = 170, b = 170) colors to two colors of your choice. If it's valentines day try to give it valentines day colors. If it's the spring, try to give it two colors that seem like spring or Easter. Or just change it to whatever you want! Click here for a slider tool to look up the RGB values of various colors!
Finished!
1. It takes a certain amount of time for the program to trace out the pattern, and more complicated patterns take longer to trace out. Here is some code you can copy into your draw() function to stop the program after a certain point and write an image file:
if ( theta > 2.0*PI) {
saveCanvas();
noLoop();
}
The problem with the code above is that it fails for cases were d is much greater than n. Modify the if statement so that the program waits longer if d >> n. Also, make sure that the program only runs as long as it needs to if n >> d.
2. Think about when n / d is an odd integer. Do you see a pattern emerging? Can you try to come up with a general formula to determine the number of petals when k is an odd integer? How many petals would you expect if you let n = 99 and d = 3?
3. Think about when n / d is an even integer. Do you see a pattern emerging? Can you try to come up with a general formula to determine the number of petals when k is an even integer? How many petals would you expect if you let n = 96 and d = 2?
4. Think about when n / d is a Half-integer. Do you see a pattern emerging? Can you try to come up with a general formula to determine the number of petals when k is a Half-integer? How many petals would you expect if you let n = 27 and d = 2?
5. What did you notice from step 6 when you changed theta += 0.005 to theta += 0.01? Why did this happen?