This programming lab is designed to illustrate the idea of wave interference. This happens because of the principle of "superposition". For sound waves, this 20 dollar word just means that if there are two speakers in a large room or open space, the amplitude of the sound waves at a particular point in that room are the sum of the waves of the two speakers.
Here is the link:
Download the file and extract it. This will create a folder with a bunch of files in it. Double click the file SoundLab.pde to open up the programming lab.
Move the speakers around. How does it change the interference pattern?
Move the little ear and notice the "log" which gives the amplitude. When you put the little ear in a place where there is destructive interference it should give amplitude close to zero. When you put it at a point of constructive interference, the amplitude should be close to 2.0.
Open up the processing interface. Go to Sketch -> Import Library -> Add Library --> scroll down to find the Sound Library --> click Install
Now download the version of the code with sound:
Extract the files. You should see a directory called SoundLab. Go into this directory and double click SoundLab.pde like usual.
Make sure to set your speaker volume low before you press play!!!
If the sound works, check that the sound gets really quiet when you put the ear in a location of destructive interference, and it gets loud if it is in a place of constructive interference.

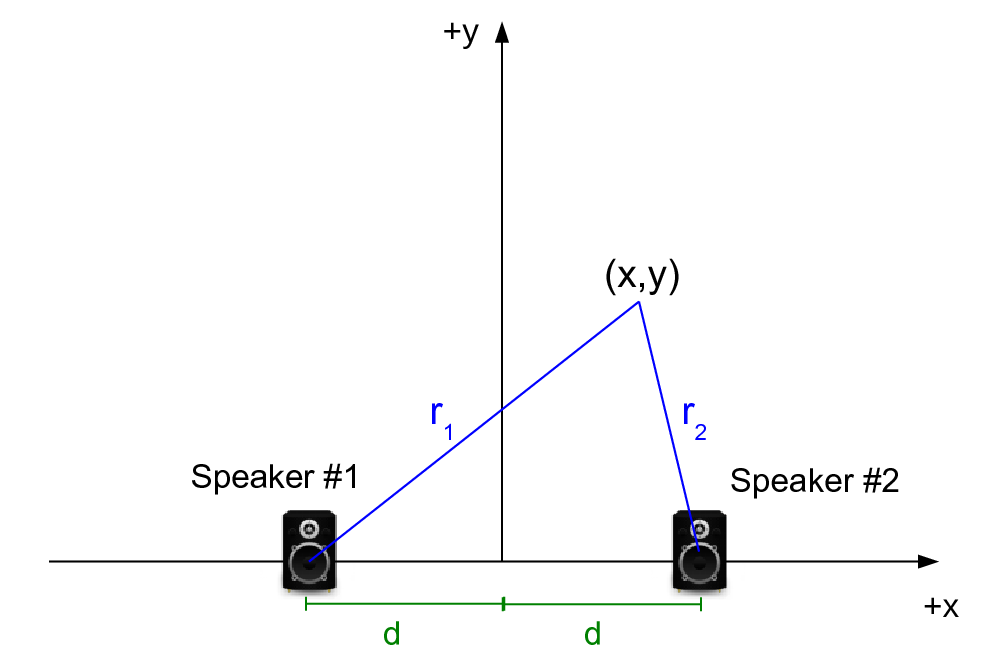
If there was just Speaker #1 the instantaneous amplitude $S_1$ at (x,y) would be this: $$S_1 = A_1 \sin (k_1 r_1 - \omega_1 t)$$
where $r_1$ is the distance between speaker #1 and the point (x,y).
Likewise, the instantaneous amplitude at (x,y) from only speaker #2 would be this: $$S_2 = A_2 \sin (k_2 r_2 - \omega_2 t)$$
where $r_2$ is the distance between speaker #2 and the point (x,y).
If you have both speakers then the amplitude at a particular point in the room would be this: $$S_1 + S_2 = A_1 \sin (k r_1 - \omega_1 t) + A_2 \sin (k r_2 - \omega_2 t)$$
As discussed on the worksheet, the following trig identity is very useful: $$\sin a + \sin b = 2 \cos \left(\frac{a-b}{2} \right) \sin \left( \frac{a+b}{2} \right)$$
As discussed on the worksheet, when you assume $A_1= A_2$, $\omega_1 = \omega_2$, one finds this: $$S_1 + S_2 = 2 A_1 \cos \left(\frac{k (r_1-r_2)}{2} \right) \sin \left(\frac{k (r_1+ r_2) - 2\omega_2 t }{2}\right)$$
and constructive/destructive interference depends on whether the cosine term works out to be eual to zero or one. How would you write $r_1$ and $r_2$ in terms of x, y and d?
Use the previous equation to explain why the following is the correct equation for destructive interference: $$|r_1 - r_2| = \frac{n\lambda}{2}$$ Why is destructive interference only achieved if $n = 1, 3, 5 , 7...$?
The previous expression turns out to be difficult to work with: $$|r_1 - r_2| = \frac{n\lambda}{2}$$ $$\sqrt{(x+d)^2 + y^2} - \sqrt{(x-d)^2 + y^2} = \frac{n\lambda}{2}$$
We'd really like to be able to solve for y, but there' no simple way of doing this. If you try to square both sides, for example, this doesn't help much to isolate y and x.
When you're stuck like this, sometimes the best you can do is approximate. Notice the following trick if $a \gg b$, $$\sqrt{a^2 + b^2 } = a \sqrt{1 + \frac{b^2}{a^2} } \approx a \left( 1 + \frac{1}{2} \frac{b^2}{a^2} \right)$$
Use this trick to prove that the lines of deconstructive interference follow this formula: $$ y = \pm \frac{4 d}{n \lambda} x $$
Modify the code to plot up the lines in the programming activity. Show that the lines for $n = 1$ match up well with the interference fringes. The result should look like this:
Plot the lines of destructive interference for n = 3, 5, 7... and compare to the simulated wave pattern. These lines will not compare as well to the simulation as it does for n = 1. Why does n > 1 compare less well to the lines of destructive interference in the simulation? Do you have any ideas for improving the locations of the lines? How could we make the approximation better?
1. Write r1 and r2 in terms of x, y and d (Step 4)
This is the primary task of Step 4.
2. Explain why destructive interference only occurs for n = 1,3,5,7... (Step 5)
This is the primary task of step 5. Why would $n = 2,4,6...$ not give destructive interference?
3. Derive $y = \pm \frac{4d }{ n \lambda }x$ from approximating the equation for destructive interference (Step 6)
This will take a couple of steps. Write these steps out on a sheet of paper, take a picture with your phone, and submit it to the assignment dropbox on canvas.
4. Submit your code with the plotted lines (Step 7)
Modify your code until it looks like the video shown in Step 7. Submit your code to the assignment dropbox on canvas.
(Optional) 5. Comment on n = 3, 5, 7...
For extra credit, modify your program to show the lines of destructive interference for n = 3, 5, 7... Explain why these lines don't compare very well to the destructive interference in the wave pattern whereas the n = 1 result does. Comment on how you would perhaps improve upon the solution $y = \pm \frac{4d}{n\lambda}x$. To be clear, there is more than one way that this solution could be improved upon.
6. Submit everything to the canvas dropbox by the deadline
Make sure to do this too!