In the classic game of Pong, there is a little ball that bounces around off various walls and objects. Importantly, the ball changes direction when it bounces but it never really slows down in speed. This is a big hint that the collisions that the ball is experiencing are elastic collisions. We'll get to what this means before too long. For now, just remember that this is a different kind of collision than we used in the "Planetoids with momentum!" coding activity. That activity focused on perfectly inelastic collisions where two objects stick together.
Click here to play with the worst version of pong ever! Notice how you can change the location of the paddle by moving the left and right arrow keys. Notice that the ball does not bounce! It is your job to fix it!
Here is the code we are starting with:
function draw(){
// Update location
x += vx*dt;
y += vy*dt;
if ( y + blob_radius > height ) {
//vx = ????; // fix this!
//vy = ????; // fix this!
}
if ( (x - blob_radius < 0) | (x + blob_radius > width) ) {
//vx = ????; // fix this!
//vy = ????; // fix this!
}
if ( (y - blob_radius < ypaddle) & abs(x - xpaddle) < paddle_width/2) {
//vx = ????; // fix this!
//vy = ????; // fix this!
}
// Move the paddle
if (keyIsDown(LEFT_ARROW)) {
xpaddle += -10;
}
if (keyIsDown(RIGHT_ARROW)) {
xpaddle += 10;
}
// Draw axes and other stuff
// This will clear the screen and re-draw it
display();
drawBlob(x,y,vx,vy,blob_radius);
drawLine(xpaddle-paddle_width/2,ypaddle,xpaddle+paddle_width/2,ypaddle);
} // end draw()
Each if statement corresponds to a bounce off of a particular thing, either the wall, the ceiling or the paddle. Let's try to figure out which part of the code is relevant to each one:
Look at this code and decide whether it is relevant to the bounce off of the wall, ceiling or the paddle:
if ( y + blob_radius > height ) {
//vx = ????; // fix this!
//vy = ????; // fix this!
}
Advice #1: Remember that blob_radius is fairly small. Does the expression if ( y > height ) make the meaning clearer?
Advice #2: If you're not sure what this does, inside of the if statement set vx = 0; and vy = 0;, then run the code and see what happens.
Advice #3: Feel free to run the code a few times! Each time you run it the blob will move in a random direction, so you may need to run it a few times before it heads in a useful direction.
Once you figure out which bounce this is referring to you can move on to the next part. Don't worry about the "fix this!" for now! We'll get to that later.
In the next if statement that we're going to look at it is important to know that the symbol | really just means OR. The following is a silly example that would never work in a real program, but hopefully it's helpful:
if ( (the teacher says I can leave early) | (the bell rings) ) {
print("I can go home");
}
Below is the actual if statement from the code. Look at this code and think about whether it is relevant to the bounce off of the wall, ceiling or the paddle:
if ( (x - blob_radius < 0) | (x + blob_radius > width) ) {
//vx = ????; // fix this!
//vy = ????; // fix this!
}
Comment: The blob_radius is overall fairly small so it may be simpler to think about the code written like this:
if ( (x < 0) | (x > width) ) {
//vx = ????; // fix this!
//vy = ????; // fix this!
}
Does this help explain which bounce this code is relevant to? If you're still not sure set vx = 0; and vy = 0;, run the code and see what happens.
We are about to look at the third if statement. It is important to know that the symbol & really just means AND. Here is a silly example that would never work in a real code:
if ( (you like physics) & (you like coding) ) {
print("Go to Ohio State and study computational physics!");
}
Now that you know what & means look at the third if statement:
if ( (y - blob_radius < ypaddle) & (abs(x - xpaddle) < paddle_width/2) ) {
//vx = ????; // fix this!
//vy = ????; // fix this!
}
This statement is even more complicated than the other two, but but let's see if we can figure out what it's relevant to. First of all, do you notice something different about the variable names here? This is the first time the variables xpaddle, ypaddle and paddle_width are used. That should be big hint for which bounce this if statement is referring to.
Inside of the if statement go ahead and set vx = 0; and vy = 0; and see what happens. You may need to run the code a few times to figure out what this code does.
The next step in the program is to figure out what to put down for vx and vy when the ball collides with a surface. But before we can do this we need to think about elastic collisions.
As discussed in the Planetoids with momentum! activity there are three different types of collisions: perfectly inelastic, inelastic and elastic. That programming activity focused on perfectly inelastic collisions where two objects stick to each other.
Both inelastic and perfectly inelastic collisions involve some loss of energy to heat or sound. However, elastic collisions lose a negligible (i.e. ridiculously small) amount energy to heat or sound which means that the total kinetic energy at the beginning (before the collision) and the end (after the collision) will be the same. So if we only have one object, and if pre-collision is $_i$ and post-collision is $_f$ this means that: $${\rm KE}_i = {\rm KE}_f$$ $$\frac{1}{2} m v_i^2 = \frac{1}{2} m v_f^2$$ $$v_i^2 = v_f^2$$
So far so good. Bear in mind that because this is a 2D problem, the initial velocity ($v_i$) and the final (post-collision) velocity ($v_f$) have an x and a y component. This means: $$v_i^2 = v_{xi}^2 + v_{yi}^2$$ $$v_f^2 = v_{xf}^2 + v_{yf}^2$$
Now we have: $$v_{xi}^2 + v_{yi}^2 = v_{xf}^2 + v_{yf}^2$$
This doesn't seem very useful yet, but in a minute it will be all we need to figure out what to put in for vx = and vy = in the various parts of the code that we have to fix.
Fun Fact: When gas particles in the air bounce off of a wall or on the ground the type of collision is elastic!
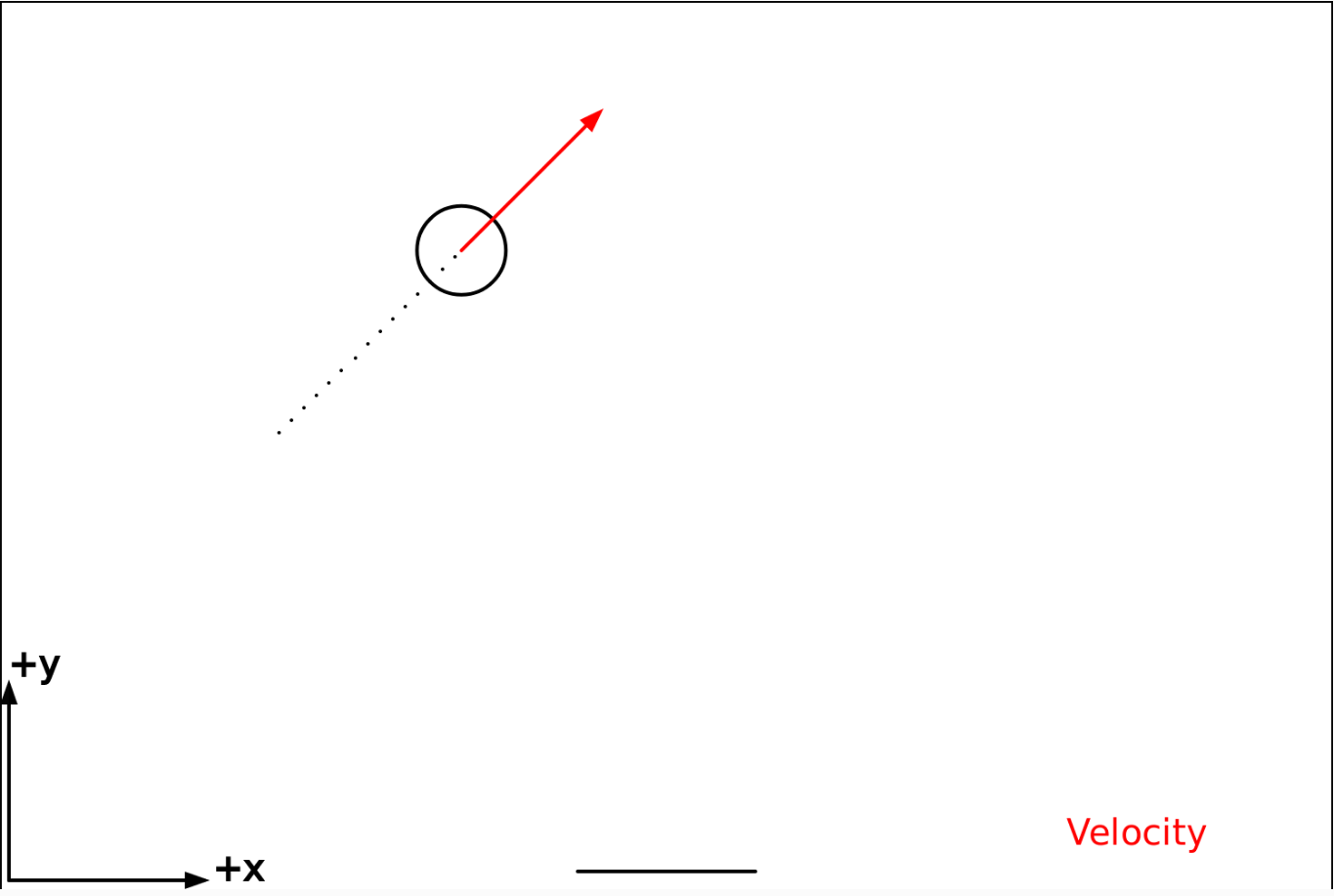
We need to figure out what to put down for vx = and vy = for the first if statement. Let's think about what the ball will be doing before the bounce happens. Here is an example:

As you can see, the ball is about to hit the top of the screen. Since the ball is traveling in the +x direction and the +y direction, let's say that $v_{xi} = 5$ and $v_{yi} = 5$.
Here's what the ball will look like after the collision:
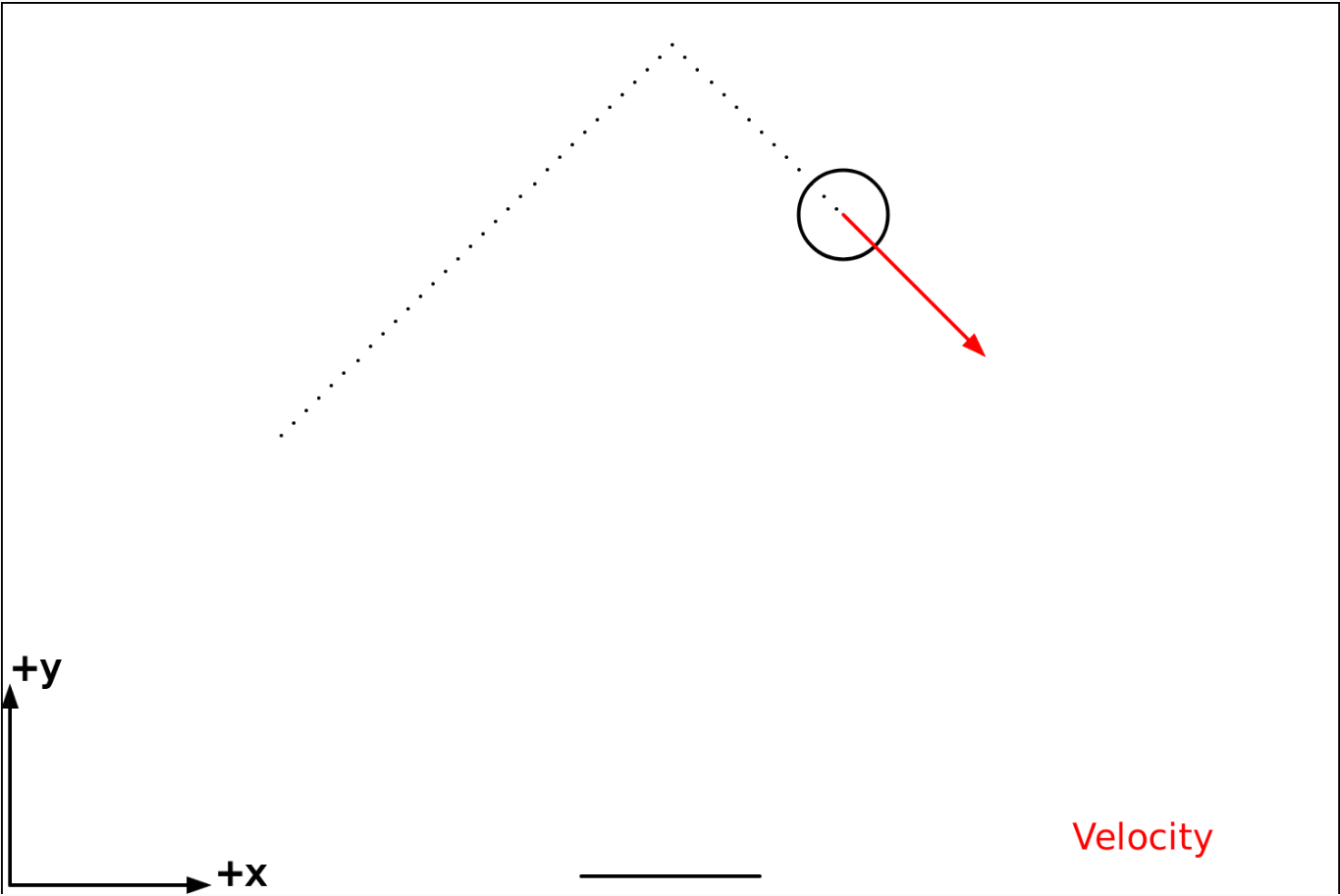
The ball is moving in the +x direction (as before) but it is now moving in the -y direction (instead of the +y direction as before). This means that $v_{xf} > 0$ and $v_{yf} < 0$.
There is one last thing that you need to know to figure out $v_{xf}$ and $v_{yf}$ and that thing is that the acceleration in this case is in the y direction (not the x direction). This means that the velocity in the x direction doesn't change: $$v_{xi} = v_{xf}$$
This means that since $v_{xi} = 5$ then $v_{xf} = 5$. Now we just need to figure out $v_{yf}$.
Just to review, earlier we learned that this is true of our collison: $$v_{xi}^2 + v_{yi}^2 = v_{xf}^2 + v_{yf}^2$$
We know that $v_{xi} = 5$ and $v_{yi} = 5$ and we learned that $$v_{xi} = v_{xf} = 5$$
This means that we have the following riddle $$5^2 + 5^2 = 5^2 + v_{yf}^2$$
Solve for $v_{yf}$. It seems pretty simple but here's the riddle: $v_{yf}$ is NOT equal to 5
Hopefully you have come to the realization that if the ball is bouncing off of the top of the screen, then, $v_{xf} = v_{xi}$ and $v_{yf} = - v_{yi}$. Sorry if this gives away the riddle. We are now ready to fix the part of the if statement that needed fixing:
if ( y + blob_radius > height ) {
vx = ????; // fix this!
vy = ????; // fix this!
}
Remember that we are in computer world (not math world) which means that expressions like vx = ????; mens that we are giving vx a new value. Since in our collison we have $v_{xf} = v_{xi}$ and $v_{yf} = - v_{yi}$ we can write:
if ( y + blob_radius > height ) {
vx = vx;
vy = -vy;
}
Try it out and see if this can get the ball to bounce like you expect. Here is how the code should behave at this stage. FYI, because the initial direction of the ball is randomized, you may need to run the code a few times in order to get the ball to head upwards.
Note: If you noticed that the line vx = vx; doesn't do anything, you're absolutely right. It's cool if you just take that line out. Makes the code shorter. Or leave it in. It's up to you.
Here again is the second if statement:
if ( (x - blob_radius < 0) | (x + blob_radius > width) ) {
vx = ????; // fix this!
vy = ????; // fix this!
}
We're not going to give you as much help with "fixing" the problem, but we will tell you that because the collision will be elastic, this expression remains true: $$v_{xi}^2 + v_{yi}^2 = v_{xf}^2 + v_{yf}^2$$
However, because the collision is in a different direction than in the first if statement, it will not work to simply copy paste what you had there into the second if statement (but you are welcome to try). (Hint: The result is still very simple, and there are minus signs involved.)
If you do this right your code should behave like this. Feel free to run the code a few times until the ball moves in a direction that helps you figure out if the bounce is working right.
Here again is the third if statement:
if ( (y - blob_radius < ypaddle) & (abs(x - xpaddle) < paddle_width/2) ) {
vx = ????; // fix this!
vy = ????; // fix this!
}
By now you have probably guessed (correctly) that this code deals with the ball bouncing off of the paddle. We're not going to just give you the answer, but you may be relieved to know that the collison is still elastic, and because the direction of the acceleration is in the y direction, the correct answer is going to look a lot like the one for the first if statement (which has the object bouncing off the top of the screen).
If the right answer still seems unclear, just try out some things and throw in some minus signs and run the program to see what happens. There's no harm in guessing. If you do it right your code should behave like this
After display(); you can add this code and it will cause the game to end if the ball gets to close to the bottom:
if (y-blob_radius < 0) {
drawText('Game Over!',0.42*width,height/2);
noLoop();
}
If you copy this into your code then your program should behave like this
After display(); you can add this code and it will show the path of the ship:
for( i = 0; i < xhistory.length ; i+= 1) {
drawPoint(xhistory[i],yhistory[i]);
}
If you copy this into your code then your program should behave like this
Feel free to make some modifications to it if you think you can make it more fun! Add barriers! Increase the initial speed!
If finished you can move on to the bonk.io game where you will add gravity to the Pong game (and end up making something even more fun!)