This programming lab is designed to illustrate the idea of wave interference. This happens because of the principle of "superposition". For sound waves, this 20 dollar word just means that if there are two speakers in a large room or open space, the amplitude of the sound waves at a particular point in that room are the sum of the waves of the two speakers.
Make sure to set your speaker volume low before you press play!!!
Click here to open up the code in an editor
If for some reason you can't open it up in the editor you can also try out the interactive at this link
Here is a version without the red line that runs faster (useful for chromebooks)
Move the little microphone around and listen to the amplitude of the tone. When you put the little microphone in a place where there is destructive interference there should be almost no sound. When you put it at a point of constructive interference, the tone should be much louder.
Move the speakers around by clicking and dragging the speakers to a new location on the x axis. How does it change the interference pattern?

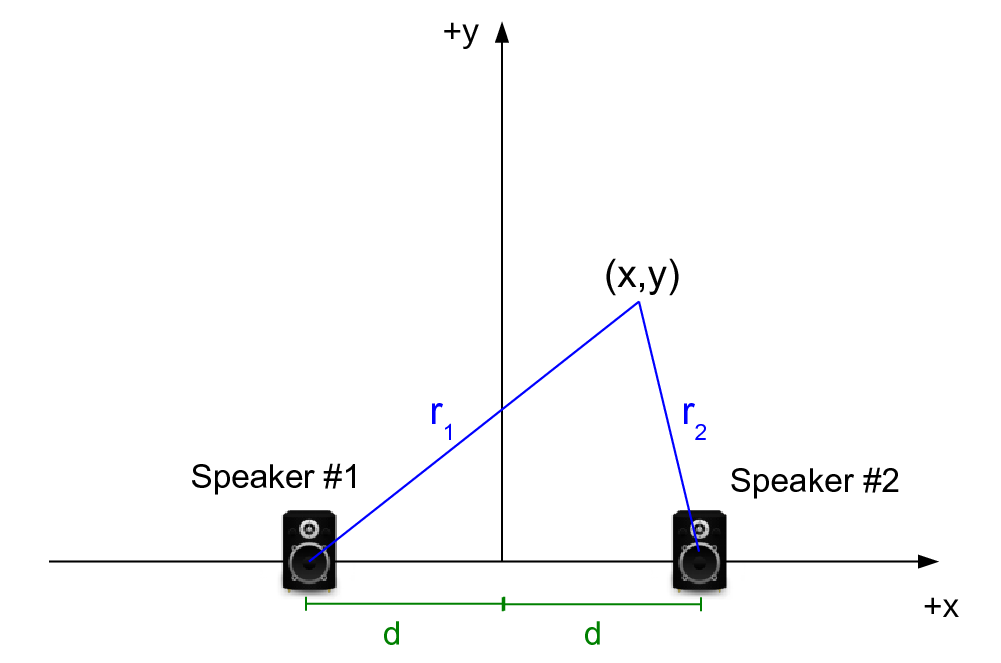
If there was just Speaker #1 the instantaneous amplitude $S_1$ at (x,y) would be this: $$S_1 = A_1 \sin (k_1 r_1 - \omega_1 t)$$
where $r_1$ is the distance between speaker #1 and the point (x,y).
Likewise, the instantaneous amplitude at (x,y) from only speaker #2 would be this: $$S_2 = A_2 \sin (k_2 r_2 - \omega_2 t)$$
where $r_2$ is the distance between speaker #2 and the point (x,y).
If you have both speakers then the amplitude at a particular point in the room would be this: $$S_1 + S_2 = A_1 \sin (k_1 r_1 - \omega_1 t) + A_2 \sin (k_2 r_2 - \omega_2 t)$$
As discussed on the worksheet, the following trig identity is very useful: $$\sin a + \sin b = 2 \cos \left(\frac{a-b}{2} \right) \sin \left( \frac{a+b}{2} \right)$$
As discussed on the worksheet, when you assume $A_1= A_2$, $\omega_1 = \omega_2$, and $k_1 = k_2$ one finds this: $$S_1 + S_2 = 2 A_1 \cos \left(\frac{k (r_1-r_2)}{2} \right) \sin \left(\frac{k (r_1+ r_2) - 2\omega t }{2}\right)$$
and constructive/destructive interference depends on whether the cosine term works out to be equal to zero or one.
Use the previous equation to explain why the following is the correct equation for destructive interference: $$|r_1 - r_2| = \frac{n\lambda}{2}$$ Why is destructive interference only achieved if $n = 1, 3, 5 , 7...$?
The previous expression turns out to be difficult to work with: $$|r_1 - r_2| = \frac{n\lambda}{2}$$ $$\sqrt{(x+d)^2 + y^2} - \sqrt{(x-d)^2 + y^2} = \frac{n\lambda}{2}$$
We'd really like to be able to solve for y, but there' no simple way of doing this. If you try to square both sides, for example, this doesn't help much to isolate y and x.
When you're stuck like this, sometimes the best you can do is approximate. Notice the following trick if $a \gg b$, $$\sqrt{a^2 + b^2 } = a \sqrt{1 + \frac{b^2}{a^2} } \approx a \left( 1 + \frac{1}{2} \frac{b^2}{a^2} \right)$$
Use this trick to prove that the lines of deconstructive interference follow this formula: $$ y = \pm \frac{4 d}{n \lambda} x $$
Modify the code to plot up the lines in the programming activity. Show that the lines for $n = 1$ match up well with the interference fringes. The result should look like this:
Move the speakers around by clicking and dragging the speakers to a new location on the x axis. Bring the speakers closer and further apart. Do your lines still match up with the interference pattern?
Plot the lines of destructive interference for n = 3, 5, 7... and compare to the simulated wave pattern. These lines will not compare as well to the simulation as it does for n = 1. Why does n > 1 compare less well to the lines of destructive interference in the simulation? Do you have any ideas for improving the locations of the lines? How could we make the approximation better?
1. Describe in words what happens when you change the separation between the speakers (Step 2b)
Click and drag the speakers closer and further apart. Describe with words what happens to the interference pattern. 2. Use the trig identify to produce the interference formula (Step 4)
Assume $A_1= A_2$, $\omega_1 = \omega_2$ and derive the equation below for the addition of two sine waves $$S_1 + S_2 = 2 A_1 \cos \left(\frac{k (r_1-r_2)}{2} \right) \sin \left(\frac{k (r_1+ r_2) - 2\omega_2 t }{2}\right)$$
3. Write r1 and r2 in terms of x, y and d (Step 5)
Advice: look closely at the diagram from Step 3 and use the pythagorean theorem.
4. Explain why destructive interference only occurs for n = 1,3,5,7... (Step 6)
This is the primary task of step 6. Why would $n = 2,4,6...$ not give destructive interference?
5. Derive $y = \pm \frac{4d }{ n \lambda }x$ from approximating the equation for destructive interference (Step 7)
This will take a couple of steps. Write these steps out on a sheet of paper, take a picture with your phone, and submit it to the assignment dropbox on canvas.
5. Submit your code with the plotted lines (Step 8)
Modify your code until it looks like the video shown in Step 8. Submit your code to the assignment dropbox on canvas.
(Optional) 6. Comment on n = 3, 5, 7...
For extra credit, modify your program to show the lines of destructive interference for n = 3, 5, 7... Explain why these lines don't compare very well to the destructive interference in the wave pattern whereas the n = 1 result does. Comment on how you would perhaps improve upon the solution $y = \pm \frac{4d}{n\lambda}x$. To be clear, there is more than one way that this solution could be improved upon.
7. Submit everything to the canvas dropbox by the deadline
Make sure to do this too!