Mathematician Katherine Johnson is famous for calculating trajectories of America's first manned space missions for Project Mercury as depicted in the movie Hidden Figures.
The big concern at that point in the history of the space program was accurately predicting where a spacecraft would land in the ocean after re-entering the earth's atmosphere. Any miscalculation could send the mercury capsule hundreds of miles from where the Navy was expecting to recover the spacecraft and the astronaut inside.
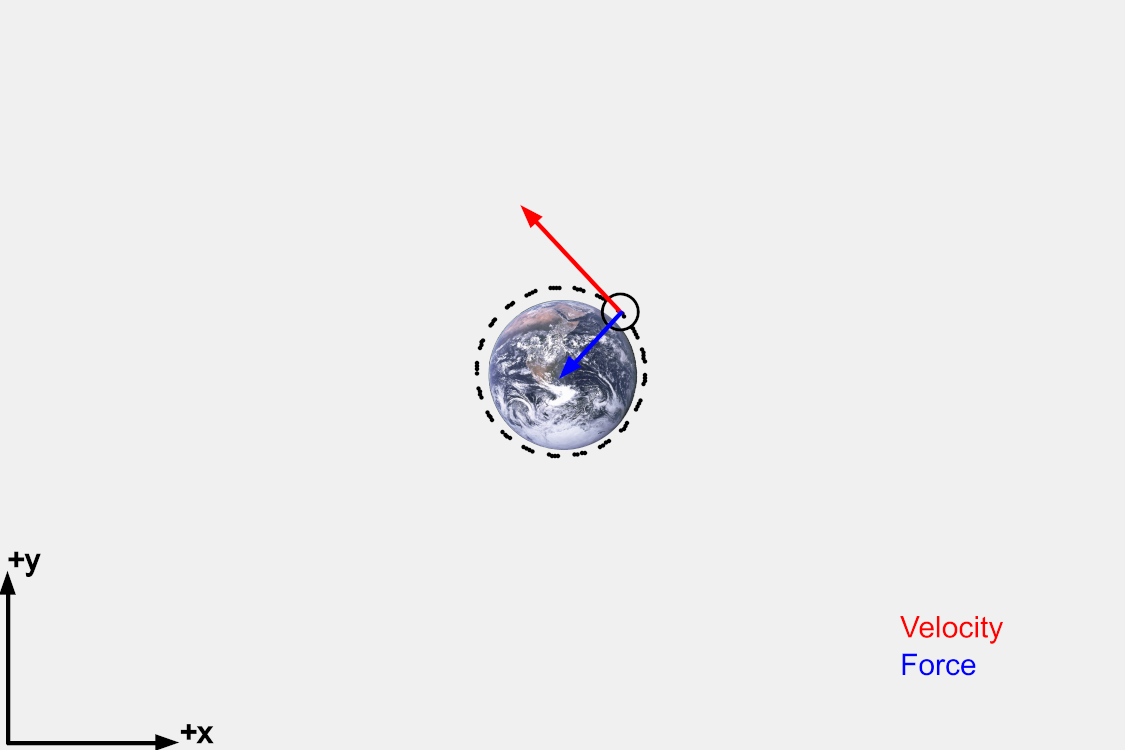
The calculation that Katherine Johnson did had to consider many different effects on the trajectory of the mercury capsule. For this activity we are going to keep it simple and start with putting the capsule in a circular orbit. Ultimately that orbit is going to look like this:

Step 0. Check out this modified version of the Slingshot with Gravity code
Click here to open up a modified version of the Slingshot with Gravity code
Step 1. Note the units
Something to notice about the program is that the units are not exactly what you would expect. For example the mass of the earth 1000 instead of $6 \cdot 10^{24}$ kg and Newton's gravitational constant is 100 instead of $6.67 \cdot 10^{-11}$. Also the radius of the earth is set to 50 instead of $6.3 \cdot 10^6$ m These constants are set in this part of the code:
// Center of the earth x_earth = 375; y_earth = 250; earth_radius = 50; M = 1000; G = 100;
You can also see there that the center of the earth in our program is at x_earth = 375; and y_earth = 250;
Although it may be a little strange to you that the units are not what they usually are, it is not unusual (both then and now) for computer programs to use unit systems that are different from the SI units you typically use in introductory physics classes. So take note of this and move on to the next step!
The main part we will be working with is at the beginning:
// Initial velocity of the Mercury capsule vx = 0; vy = 30; // Initial position of the Mercury capsule x = 430; y = 250;
This part of the code determines the "initial" position and velocity of the mercury capsule. The word "initial" is in quotes here because these numbers are really the position of the rocket a few minutes after launch.
Notice that when you run the code, the mercury capsule comes back to earth pretty quickly because the initial velocity is too low and you get a "Welcome back to Earth!" message on screen.
Clearly vy = 30; is too slow and the mercury capsule is coming to earth too soon. The goal of Project Mercury is to make multiple orbits of the earth before coming back down.
Increase vy from 30 to larger values until you get a perfectly circular orbit like this example
Write down the number you get for the value of vy that gives you this orbit!
One of the things Katherine Johnson had to do was double check the results of the computer simulation. Back then (and in many ways this is still true) it was always possible that the computer simulation miscalculated something or the people who set up the computer program made some subtle mistake. Famously, John Glenn wanted someone (a person!) to confirm the prediction from the computer simulation for the Mercury mission.
Let's imagine that the program we just ran is being scrutinized by the engineers and astronauts. We should confirm the two results we just found (1) that vy = 30 is too slow to orbit the earth, and (2) that a larger value (which you wrote down) is what we need.
Katherine Johnson knew her physics! In physics it is always good to start with Newton's 2nd law which relates the forces to the mass and acceleration of an object. $$ F = m a $$
In this situation the only force we are considering is the force of gravity: $$ F_{\rm grav} = \frac{GMm}{r^2} $$
where $m$ is the mass of our object, in this case the Mercury capsule. This means that the acceleration due to gravity is this: $$ a_{\rm grav} = \frac{G M }{r^2} $$
This acceleration does not necessarily cause objects to move in a perfect circle. The acceleration of any object moving along a curve is given by this equation: $$ a_{\rm curve} = \frac{v^2}{r_{\rm curve}} $$
where $r_{\rm curve}$ is the radius of curvature and $v$ is the speed. Since the mercury capsule is going to follow some kind of curve we can set these accelerations equal to each other: $$ a_{\rm grav} = a_{\rm curve} $$ $$ \frac{GM}{r^2} = \frac{v^2}{r_{\rm curve}} $$
You will use this equation in Steps 4b and 4c
Earlier we found that setting vx = 0; vy = 30; for our initial value resulted in the mercury capsule landing back on earth too soon instead of making an orbit. Mathematically this implies that: $$ r_{\rm curve} < r_{\rm earth} $$
You are the computer! Use the equation at the end of 4a to calculate $r_{\rm curve}$ and show that it is less than $r_{\rm earth}$ which in the program is 50.
Advice: The speed $v$ is $v = \sqrt{v_x^2 + v_y^2} $
Challenge: Don't use a calculator to do this! Do it by hand. Use long division if you have to! Katherine Johnson didn't have a calculator!
Earlier in Step 3 you increased vy until the mercury capsule had a stable circular orbit. Hopefully you wrote that number down.
Now use the equation at the end of Step 4a, but instead of using $v = 30$, solve for $v$ assuming that $r_{\rm curve} = r = r_{\rm earth} = 50$.
Challenge #1: Calculate $v$ without using a calculator! Do the long division by hand! Calculate the square root without a calculator too! Katherine Johnson didn't have a calculator!
Challenge #2: Improve the estimate for $v$ by noticing that in the program the mercury capsule is not exactly at $r = r_{\rm earth} = 50$. If you look closely, you will see that it is orbiting at a slightly larger radius than that (which is similar to how the Mercury capsule would have orbited, many miles above the earth's surface). By taking this into account you can get a more accurate estimate of $v$
The engineers and the astronauts want to know the percent error between your calculation and the computer program. For understandable reasons they don't trust the computer simulation.
Calculate the percent error on the velocity you calculated in 4b like this: $$ \% = 100 \cdot \frac{|\rm meas - true|}{ \rm true} $$
Treat your calculation of $v$ in 4c as true and the computer program's estimate for $v$ that you found in Step 3 as measured.
What do you get for the percent error?
Challenge: The engineers and astronaut John Glenn need you to be as precise as you can! See if you can improve the agreement between the calculation of $v$ and the measurement of $v$ from the program from Step 3. Try to get more digits of precision on $v$ in Step 3 and/or do challenge #2 at he end of Step 4c to get a more precise value.