In considering the many body problem of the nucleus, the independent
particle model is often used as a starting point. In the independent
particle model (IPM) the nucleons in the nucleus are taken to be
non-interacting (uncorrelated) particles moving in some mean field
potential. An occupation of the
lowest single-particle states up to, and not beyond, the Fermi energy
describes the ground state.
This model has been successful in describing the shell structure of the
nucleus and in describing the characteristics of single particle
excitations, but in order to describe collective phenomena one needs to
also consider the residual two-body interactions between nucleons which
are not accounted for in the mean-field potential. It is these
residual interactions which give rise to collectivity in the nucleus.
Excitations of the ground state are described in terms of particle-hole
excitations in which a nucleon in some state, k, below the Fermi surface
is promoted to a state, m, above
it. The Hamiltonian of these excitations is
given by:
where 
and a are the creation and annihilation operators,
respectively, 
is the ground state energy of the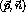 
nucleon, and 
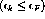is the particle-hole
interaction.
If the independent particle model does a fairly good job of describing the ground state nucleus then the Random Phase Approximation (RPA), which cuts off the excitations at the one-particle/one-hole (1p-1h) level, will give a good description of the nuclear excitation. The 1p-1h excitations in RPA can be formally defined by the operator
where,
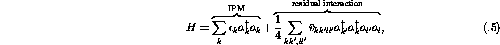
The index m(i) indicates a state below(above) the fermi surface.
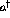and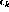 
are the forward and backward-going p-h amplitudes,
respectively.
Physically the squares of these amplitudes represent the probability of finding a given p-h excitation in the final state,
The equation of motion for 
,
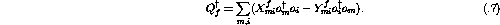
after linearization can be written as [Ost92]
which is the standard RPA equation. The matrix elements are given by
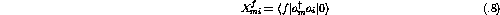
It is obvious that a calculation of the excitation spectrum is highly
dependent on the residual p-h interaction. Generally, RPA provides a valid
description of nuclear excitations providing that the backward-going
amplitudes, 
, are small compared to the forward-going amplitudes,
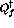. If the former are large it is an indication that the ground
state will deviate significantly from the independent particle model due to
2p-2h and higher order excitations. In other words the residual
interaction is causing large ground state correlations.