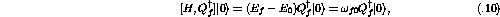
As a result of the symmetry properties of the nuclear force the form of the particle-hole interaction can be written as the sum of terms with different spin and isospin dependence. For the specific case of isospin symmetric nuclear matter the p-h force has the form [Ost92]
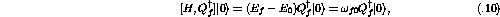
In the so-called Landau limit, which describes small excitations near the
Fermi surface, the particle and hole momenta, 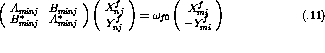 and
and 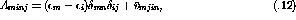 , are both near the Fermi momentum and thus roughly
equal to each other in magnitude. Therefore, the interaction terms will only
depend on the angle between
, are both near the Fermi momentum and thus roughly
equal to each other in magnitude. Therefore, the interaction terms will only
depend on the angle between  and
and 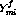 and can
be expanded in terms of Legendre polynomials,
and can
be expanded in terms of Legendre polynomials, 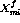 . For very short range interactions only the first few terms in
the expansion will be significant, and for contact interactions only the
l=0 term is important. Therefore, for zero-range interactions the
Landau-Migdal
theory for effective p-h interactions is usually written as
. For very short range interactions only the first few terms in
the expansion will be significant, and for contact interactions only the
l=0 term is important. Therefore, for zero-range interactions the
Landau-Migdal
theory for effective p-h interactions is usually written as
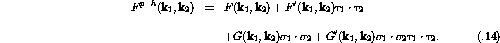
where the radial dependence of the 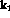 term is given by the nuclear
charge distribution and
term is given by the nuclear
charge distribution and 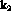 is the inverse of the density of state,
is the inverse of the density of state,
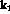 302 MeV
302 MeV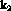 where
where 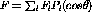 is the Fermi momentum and
is the Fermi momentum and 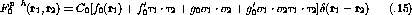 is the quasiparticle
effective mass.
is the quasiparticle
effective mass.