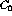 meson is also included as the other
isovector meson which could contribute the p-h force will take the form
[Ost92]
meson is also included as the other
isovector meson which could contribute the p-h force will take the form
[Ost92]
In order to correct the Landau-Migdal interaction to account for the finite
range of the NN interaction the contribution due to meson exchange can be
included explicitly. This correction would seem to be especially important
in the spin-isospin channel because of the contribution of the lightest
meson, the pion. If the 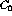 meson is also included as the other
isovector meson which could contribute the p-h force will take the form
[Ost92]
meson is also included as the other
isovector meson which could contribute the p-h force will take the form
[Ost92]

where 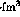 is a phenomenological constant related to the
Landau-Migdal parameter
is a phenomenological constant related to the
Landau-Migdal parameter 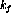 . The
. The 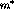 and
and 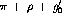 exchange terms
do not describe well the short range behavior of the interaction so it is
necessary to keep the contact term, which accounts for heavy meson and QCD
effects. This is the so-called
exchange terms
do not describe well the short range behavior of the interaction so it is
necessary to keep the contact term, which accounts for heavy meson and QCD
effects. This is the so-called 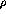 model for the
isovector p-h interaction.
model for the
isovector p-h interaction.
In momentum space the particle-hole potential for the
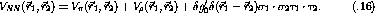 model is given by [ETB85]
model is given by [ETB85]
where 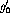 is the meson-nucleon coupling constant
is the meson-nucleon coupling constant  ,
,
 is the energy loss, q is the momentum transfer,
is the energy loss, q is the momentum transfer, 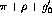 is the
meson mass, and
is the
meson mass, and 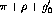 is the monopole vertex form factor which takes
the form [OTW82]
is the monopole vertex form factor which takes
the form [OTW82]
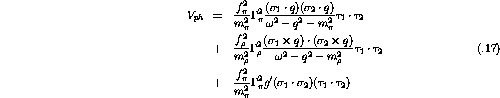
The cut-off mass, 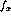 , is inversely related to the range of the
meson-nucleon vertex and must be determined phenomenologically from the
short range behavior. It is obvious from equation
, is inversely related to the range of the
meson-nucleon vertex and must be determined phenomenologically from the
short range behavior. It is obvious from equation ![]() that,
because of its pseudoscalar nature, the pion is primarily responsible
for the spin-longitudinal
that,
because of its pseudoscalar nature, the pion is primarily responsible
for the spin-longitudinal 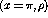 response while the
response while the
 part dominates the spin-transverse
part dominates the spin-transverse 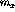 response.
response.
Through use of the identity 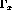 we can separate equation
we can separate equation ![]() into
the spin-longitudinal and spin-transverse parts [McC92]:
into
the spin-longitudinal and spin-transverse parts [McC92]:
where 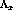 .
.
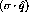
Figure: The momentum transfer dependence of the residual
particle-hole interaction due to 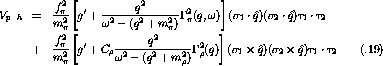 and
and 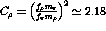 meson exchange. The
dashed line shows the
meson exchange. The
dashed line shows the  dependence and the
dotted line shows the
dependence and the
dotted line shows the 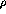 dependence of the interaction. [Pro91]
dependence of the interaction. [Pro91]
The separate spin-longitudinal and spin-transverse parts of the
particle-hole force are plotted in figure ![]() with
with 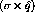 ,
,
 GeV,
GeV, 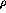 GeV, and
GeV, and 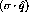 .
Both components of the force are repulsive at short range, but, due to the
small pion mass, the spin-longitudinal part becomes attractive at around 1
.
Both components of the force are repulsive at short range, but, due to the
small pion mass, the spin-longitudinal part becomes attractive at around 1
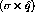 while the transverse part remains repulsive until
while the transverse part remains repulsive until 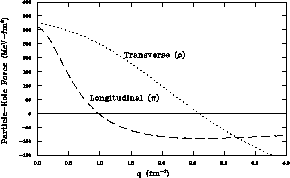 . Therefore, using
the
. Therefore, using
the 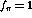 model for the residual particle-hole
interaction in their RPA calculations, Alberico et al. [AEM82]
predicted the transverse response would be quenched and hardened while the
longitudinal response is softened and enhanced, particularly between
model for the residual particle-hole
interaction in their RPA calculations, Alberico et al. [AEM82]
predicted the transverse response would be quenched and hardened while the
longitudinal response is softened and enhanced, particularly between
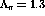 to
to 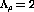 . This means that the ratio of the
longitudinal to the transverse responses should be larger at small energy
loss
. This means that the ratio of the
longitudinal to the transverse responses should be larger at small energy
loss  in nA collisions than in nn collisions, as shown in figure
in nA collisions than in nn collisions, as shown in figure
![]() .
.