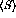 meson, will decrease with increasing
density at about the same rate [BSH91]:
meson, will decrease with increasing
density at about the same rate [BSH91]:
One of the more interesting explanations for the suppression of the pion
field, and the corresponding lack of enhancement in the longitudinal
response, at short distance scales is the partial restoration of chiral
invariance with density [Bro95]. Essentially, this means that the
masses of hadrons comprised of up and down quarks, and in particular the
vector mesons such as the 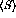 meson, will decrease with increasing
density at about the same rate [BSH91]:
meson, will decrease with increasing
density at about the same rate [BSH91]:
In equation ![]() the quantities with the asterisk are the density
modified values and those without are free space values.
the quantities with the asterisk are the density
modified values and those without are free space values. 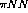 is the
pion decay constant, but in this context serves a more basic role; it is
the order parameter for chiral symmetry breaking.
is the
pion decay constant, but in this context serves a more basic role; it is
the order parameter for chiral symmetry breaking.
The argument for the validity of the relationship in equation ![]() has been made in [BrR91]. Essentially the argument states that the
structure of free space Lagrangians is constrained by symmetries
inherent to QCD and that even as density increases those symmetries, and
therefore the form of the Lagrangian, will remain the same. As density
increases and the nature of the vacuum changes, if the Lagrangian does not
change then the coupling constants and masses must be modified according
to QCD constraints to account for the effects of a modified vacuum (i.e.
the altered quark condensate
has been made in [BrR91]. Essentially the argument states that the
structure of free space Lagrangians is constrained by symmetries
inherent to QCD and that even as density increases those symmetries, and
therefore the form of the Lagrangian, will remain the same. As density
increases and the nature of the vacuum changes, if the Lagrangian does not
change then the coupling constants and masses must be modified according
to QCD constraints to account for the effects of a modified vacuum (i.e.
the altered quark condensate  ). The
details
are described in [BrR91] at the mean field level for which the
relationship in equation
). The
details
are described in [BrR91] at the mean field level for which the
relationship in equation ![]() is exact. Higher order loop
correction will have some effect which leads to the use of the approximate
signs [Bro95].
The pion mass is the exception to this new scaling law because of its
special status as a Goldstone boson. The pion mass has actually been shown
to increase slightly, but not significantly, with increased density
because of a slightly repulsive optical potential [ErW88].
is exact. Higher order loop
correction will have some effect which leads to the use of the approximate
signs [Bro95].
The pion mass is the exception to this new scaling law because of its
special status as a Goldstone boson. The pion mass has actually been shown
to increase slightly, but not significantly, with increased density
because of a slightly repulsive optical potential [ErW88].
It was the differences in the mass of the pion and 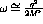 meson
that caused the differences between the transverse and longitudinal pieces
of the particle-hole potential (eqn.
meson
that caused the differences between the transverse and longitudinal pieces
of the particle-hole potential (eqn. ![]() ) illustrated in figure
) illustrated in figure
![]() . The results of some calculations based on QCD sum rules
[HaL92] are
shown in figure
. The results of some calculations based on QCD sum rules
[HaL92] are
shown in figure ![]() show that, for nuclear matter density,
show that, for nuclear matter density,

is a reasonable ratio for the reduction of the in-medium 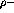 mass.
mass.
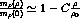
Figure: The  meson mass as a function of density
meson mass as a function of density 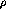 ;
based on QCD sum rule calculations. Functional form is
;
based on QCD sum rule calculations. Functional form is
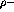 , where
, where
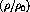 . The deviation from linearity is the result of an
uncertainty in the calculation [HaL92].
. The deviation from linearity is the result of an
uncertainty in the calculation [HaL92].
This would account for the difference between the transverse and
longitudinal responses and bring 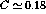 close to
unity [BrW94]. In fact, because of the surface peaked nature of the
close to
unity [BrW94]. In fact, because of the surface peaked nature of the
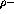 reaction the density sampled will actually be
reaction the density sampled will actually be 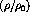 which means
which means 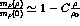 which could not
fully account for the results in previous
which could not
fully account for the results in previous 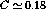 experiments.
experiments.
The analysis of several recent heavy-ion experiments lend support to the
idea that
the 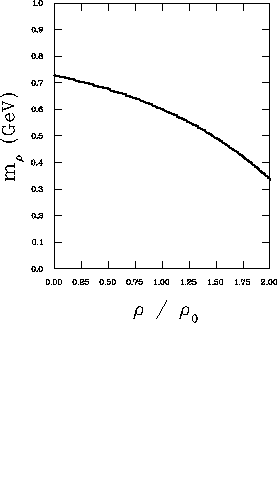 meson mass decreases with density [LKB95] [LKB96].
Models based on the medium modification of vector meson properties have
been relatively successful at fitting data from heavy-ion collision
(S + Au) at the CERN SPS at 200 GeV/nucleon. The dilepton invariant
mass spectrum from these experiments show an
excess of dileptons between 250 MeV and 1 GeV over that from proton-nucleus
collisions, which has been quantitatively explained by the reduction in
vector meson masses in the dense medium [LKB95] [LKB96].
meson mass decreases with density [LKB95] [LKB96].
Models based on the medium modification of vector meson properties have
been relatively successful at fitting data from heavy-ion collision
(S + Au) at the CERN SPS at 200 GeV/nucleon. The dilepton invariant
mass spectrum from these experiments show an
excess of dileptons between 250 MeV and 1 GeV over that from proton-nucleus
collisions, which has been quantitatively explained by the reduction in
vector meson masses in the dense medium [LKB95] [LKB96].