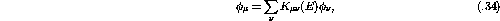
The Green's-function Monte Carlo (GFMC) technique [Kal62] has been successfully used to study ground-state properties in a variety of many-body systems. The GFMC employs a Monte Carlo technique to iterate the integral equation
where 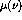 is the ground state energy, and
is the ground state energy, and 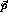 is
the Green's function defined by
is
the Green's function defined by
Here  are the coordinates of the
N particles in the system,
are the coordinates of the
N particles in the system, 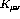 is the wave function after n
iterations, and
is the wave function after n
iterations, and 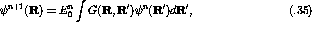 is the ground state energy of that wave function.
The Hamiltonian, H, will be described by conventional
nuclear theory
is the ground state energy of that wave function.
The Hamiltonian, H, will be described by conventional
nuclear theory
where 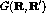 and
and  are given by realistic models of nuclear
potentials such as the Argonne and Urbana models, respectively, as
described in [WSA84].
The initial wave function and energy,
are given by realistic models of nuclear
potentials such as the Argonne and Urbana models, respectively, as
described in [WSA84].
The initial wave function and energy, 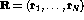 and
and 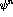 are typically obtained by variational techniques [PaW79].
It is not usually feasible to solve equation
are typically obtained by variational techniques [PaW79].
It is not usually feasible to solve equation ![]() directly.
However, all that is required is a technique for sampling
directly.
However, all that is required is a technique for sampling
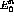 for random
for random  for a given
for a given  .
Then Monte Carlo techniques can be applied, using
.
Then Monte Carlo techniques can be applied, using
 as a density function for
as a density function for 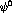 conditional upon
conditional upon
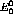 . Each iteration of equation
. Each iteration of equation ![]() may be considered a
step in a continuous random walk [Kal62].
may be considered a
step in a continuous random walk [Kal62].
A form of the GFMC method is particularly suitable for treating the
complicated spin-isospin structure of few body systems [CaS92]. The
GFMC is used to project out the ground state from an initial trial function,
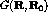 , using the imaginary time propagator [Car91]:
, using the imaginary time propagator [Car91]:

Generally, 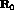 can not be directly computed, but by dividing the
propagation time,
can not be directly computed, but by dividing the
propagation time, 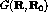 , into small steps:
, into small steps:
The full propagator can be evaluated by choosing an accurate approximation for the short time propagator and using Monte Carlo techniques to sample the propagator.
The Euclidean response of a nucleus to some operator, 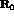 , is the Laplace
transform of the nuclear response,
, is the Laplace
transform of the nuclear response, 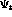 , as a function of imaginary time
[Pan94]:
, as a function of imaginary time
[Pan94]:
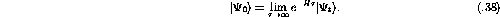
where A is the number of nucleons, q is momentum transfer, 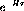 is
energy loss, and
is
energy loss, and  is a constant. The nuclear response is defined as
is a constant. The nuclear response is defined as
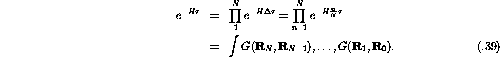
where 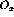 and
and 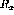 are the ground state and
eigenstates of the system with energies of
are the ground state and
eigenstates of the system with energies of 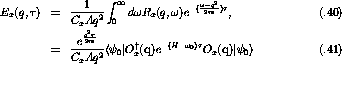 and
and  ,
respectively. If we consider the longitudinal and transverse spin-isospin
operators
,
respectively. If we consider the longitudinal and transverse spin-isospin
operators 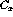 :
:
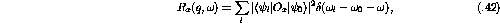
then 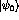 and
and 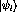 .
.
If accurate descriptions of the ground state wave functions,
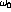 , obtained from variational Monte Carlo techniques
[Wir91], are used the Euclidean response can be calculated
[Pan94]:
, obtained from variational Monte Carlo techniques
[Wir91], are used the Euclidean response can be calculated
[Pan94]:

where 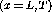 is the propagator:
is the propagator:
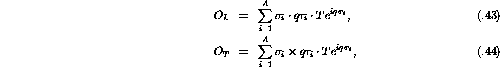
To carry out the integrations over 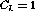 and
and 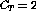 the
propagator is considered to be the product of short-time propagators
the
propagator is considered to be the product of short-time propagators
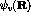 where n goes from 1 to
N as defined in equation
where n goes from 1 to
N as defined in equation ![]() . These short-time propagators can
be approximated accurately enough as [Car91]
. These short-time propagators can
be approximated accurately enough as [Car91]
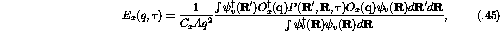
and are sampled by Monte Carlo techniques.
The Green's function Monte Carlo techniques have been used to calculate the
Euclidean proton response functions on A=3 and A=4 systems
[Car91] [CaS92]. These calculations show that the inclusion of
two-body exchange current operators can cause significant effects even at a
relatively low momentum transfer. A comparison of the calculations to
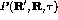 experimental data shown that
two-body mechanisms are necessary to reproduce the experimental results.
In particular, calculations of
experimental data shown that
two-body mechanisms are necessary to reproduce the experimental results.
In particular, calculations of 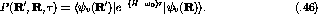 quasifree
scattering showing a large enhancement in the transverse channel due to the
exchange currents were well supported by experiment [CaS92].
quasifree
scattering showing a large enhancement in the transverse channel due to the
exchange currents were well supported by experiment [CaS92].
Recently the GFMC techniques have been used [Pan94] to calculate
the spin isospin nuclear responses in light nuclei, 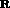 and
and
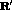 , in light of the lack of expected enhancement in the nuclear
longitudinal to transverse response ratio. The calculations indicate that
an enhancement should exist, even in the lightest nuclei, but it may be
moved out to the high excitation energy tail of the quasifree distribution.
These new calculations provide an excellent motivation for
a measurement of spin isospin responses in deuterium.
, in light of the lack of expected enhancement in the nuclear
longitudinal to transverse response ratio. The calculations indicate that
an enhancement should exist, even in the lightest nuclei, but it may be
moved out to the high excitation energy tail of the quasifree distribution.
These new calculations provide an excellent motivation for
a measurement of spin isospin responses in deuterium.