



Next: The Nucleon-Nucleon Frame
Up: FORMALISM
Previous: FORMALISM
The spin structure of the 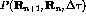 reaction is given by
reaction is given by
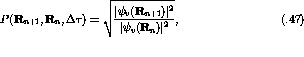 , where A
and B represent the spin of the target's initial and final
states, respectively.
The derivations in this section are made for the case of a spinless
target, but the resulting relations hold for the more general case. The
complete derivation for arbitrary projectile and target spin can be found
in [Wol56]. Details on the method used here can be found in
[Ohl72].
, where A
and B represent the spin of the target's initial and final
states, respectively.
The derivations in this section are made for the case of a spinless
target, but the resulting relations hold for the more general case. The
complete derivation for arbitrary projectile and target spin can be found
in [Wol56]. Details on the method used here can be found in
[Ohl72].
In non-relativistic quantum mechanical scattering one can define a
transformation matrix M which contains all the spin related information
in a reaction. The outgoing nucleon spinor 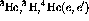 is related to the
incident nucleon spinor
is related to the
incident nucleon spinor 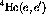 linearly by the relationship
linearly by the relationship

The expectation value of an observable corresponding to a given
Hermitian operator, 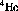 , is
, is

for some given 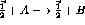 . That spinor represents a single particle of
definite polarization. It is possible to define a density matrix,
. That spinor represents a single particle of
definite polarization. It is possible to define a density matrix,
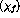 , such that
, such that

where  means the trace of the argument.
means the trace of the argument.
If we want to work with a large ensemble of particles, such as in an
experiment, it is necessary to find the ensemble average of the expectation
value, 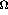 , defined as
, defined as
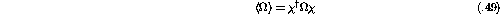
where N is the total number of particles. Working with the ensemble
average of the expectation value is necessary because the spinors
describing the individual particles will not likely be identical. That is,
the polarization of the individual particles may vary from one particle to
the next. In this case it is
still possible to define a density matrix:

such that

For the remainder of this chapter the ``ensemble'' will be understood and
the overline notation will be not be used.
The average polarization of an ensemble can be found by applying the
standard Pauli matrices:
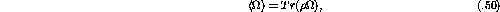
as the Hermitian operators. Therefore,

The density matrix can be rewritten in terms of the polarization by
realizing that the density matrix, being Hermitian itself, can be
represented in terms of the set I, 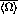 ,
,  ,
,  :
:
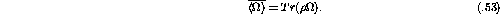
where j = 0,x,y,z and 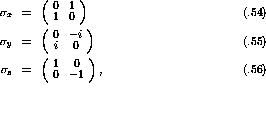 is the unit matrix
is the unit matrix
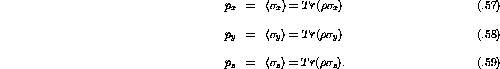
Using the identity 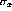 , the
coefficients,
, the
coefficients, 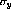 , are
, are

The density matrix can then be written as:
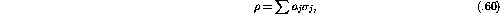
assuming the density matrix is normalized such that

Given the definition in equation  the relationship between the
initial and final spinors shown in equation
the relationship between the
initial and final spinors shown in equation  can be rewritten as
can be rewritten as
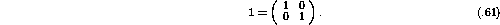
If 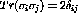 is normalized to unity the differential cross section, I,
for a polarized beam is given by
is normalized to unity the differential cross section, I,
for a polarized beam is given by

If the beam is unpolarized,
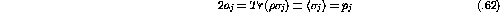
then the expression reduces to the standard definition for unpolarized
cross section:
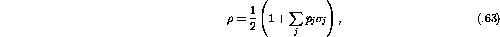
Using the definition for  (eqn.
(eqn.  ) in equation
) in equation  one finds
one finds
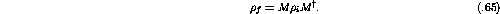
which, in turn, yields

where the analyzing power, 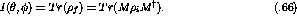 , is defined as
, is defined as
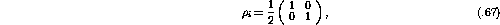
If we wish to also consider the polarization of the scattered particles it
is useful to note that  is normalized to unity so that
is normalized to unity so that

where the prime indicates the outgoing particle.
Therefore,
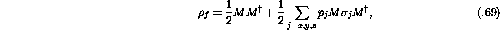
Once again using eqn.  this becomes
this becomes
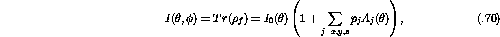
where 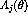 is the
is the  component of the polarization
that scattered particle would have if the beam were unpolarized
(called induced polarization), and
component of the polarization
that scattered particle would have if the beam were unpolarized
(called induced polarization), and
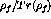 is the polarization transfer coefficient which
relates the
is the polarization transfer coefficient which
relates the 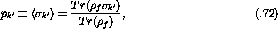 initial polarization component to the
initial polarization component to the 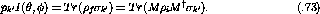 final
polarization component.
final
polarization component. 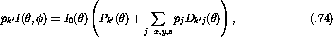 and
and
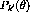 are defined as:
are defined as:

and

In their fully expanded forms the expressions for cross section and
polarization are:

which is the most general form of the expressions allowed by conservation
of angular momentum despite the fact that we initially made the assumption
of a spinless target.
The next step in the derivation is to consider the restriction imposed on
the polarization observables imposed by parity conservation and time
reversal invariance.
Under a parity transformation all vector quantities should reverse sign
while pseudovectors, such as a polarization, should be unaffected.
Therefore the initial and final momentum vectors, 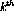 and
and
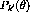 respectively, being vector quantities will change sign.
Assume the particle motion is defined as being along the z-axis, and
the scattering plane
is defined by the x- and z-axes. Under a parity transformation
the in-plane coordinates, being
defined by linear combinations of
respectively, being vector quantities will change sign.
Assume the particle motion is defined as being along the z-axis, and
the scattering plane
is defined by the x- and z-axes. Under a parity transformation
the in-plane coordinates, being
defined by linear combinations of 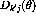 and
and 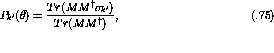 ,
will rotate
,
will rotate 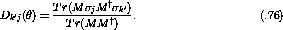 .
The y-axis will be
perpendicular to the scattering plane (in the
.
The y-axis will be
perpendicular to the scattering plane (in the 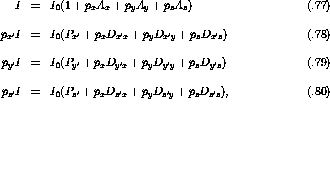 direction) and will not change sign under this
transformation. The polarization transfer coefficients which relate
polarization vectors in the scattering plane will be allowed by parity
conservation
because after the parity transformation the reaction will look exactly
the same as before. Actually, to be precise, the
reaction will look as though both the ingoing and outgoing polarization
vectors are reversed, but the linear nature of equations
direction) and will not change sign under this
transformation. The polarization transfer coefficients which relate
polarization vectors in the scattering plane will be allowed by parity
conservation
because after the parity transformation the reaction will look exactly
the same as before. Actually, to be precise, the
reaction will look as though both the ingoing and outgoing polarization
vectors are reversed, but the linear nature of equations  to
to
 means that the two cases are equivalent. Therefore,
means that the two cases are equivalent. Therefore,
 ,
,  ,
, 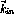 , and
, and
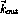 are allowed by conservation of parity. On the other hand,
if one of the polarization vectors is out of the plane (y-axis) then that
polarization vector will not change since the parity transform is closely
related to a
are allowed by conservation of parity. On the other hand,
if one of the polarization vectors is out of the plane (y-axis) then that
polarization vector will not change since the parity transform is closely
related to a 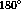 rotation around the y-axis. Because the
in-plane polarization vector changes sign, as described above, then those
coefficients must obey
rotation around the y-axis. Because the
in-plane polarization vector changes sign, as described above, then those
coefficients must obey 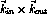 for parity to be conserved, and
so those terms must be identically zero. Finally, because the parity
transformation
doesn't affect the out-of-plane polarization vectors at all
for parity to be conserved, and
so those terms must be identically zero. Finally, because the parity
transformation
doesn't affect the out-of-plane polarization vectors at all
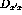 will be allowed. For similar reasons
will be allowed. For similar reasons 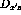 and
and 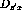 are
the only components of analyzing power and induced polarization that are
non-zero. Therefore equations
are
the only components of analyzing power and induced polarization that are
non-zero. Therefore equations  to
to  reduce to:
reduce to:

Recasting these equations into a single matrix equation defining the
resultant polarization vector:





Next: The Nucleon-Nucleon Frame
Up: FORMALISM
Previous: FORMALISM
Michael A. Lisa
Tue Apr 1 08:52:10 EST 1997
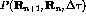 reaction is given by
reaction is given by
 , where A
and B represent the spin of the target's initial and final
states, respectively.
The derivations in this section are made for the case of a spinless
target, but the resulting relations hold for the more general case. The
complete derivation for arbitrary projectile and target spin can be found
in [Wol56]. Details on the method used here can be found in
[Ohl72].
, where A
and B represent the spin of the target's initial and final
states, respectively.
The derivations in this section are made for the case of a spinless
target, but the resulting relations hold for the more general case. The
complete derivation for arbitrary projectile and target spin can be found
in [Wol56]. Details on the method used here can be found in
[Ohl72].
 is related to the
incident nucleon spinor
is related to the
incident nucleon spinor  linearly by the relationship
linearly by the relationship

 , is
, is

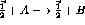 . That spinor represents a single particle of
definite polarization. It is possible to define a density matrix,
. That spinor represents a single particle of
definite polarization. It is possible to define a density matrix,
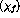 , such that
, such that

 means the trace of the argument.
means the trace of the argument.
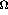 , defined as
, defined as
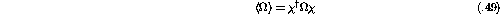


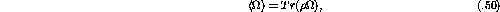

 ,
,  ,
,  :
:
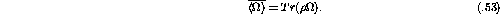
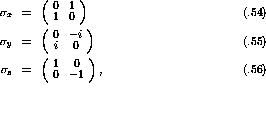 is the unit matrix
is the unit matrix
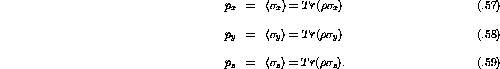
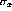 , the
coefficients,
, the
coefficients, 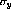 , are
, are

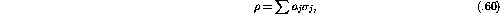

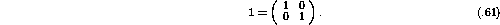
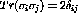 is normalized to unity the differential cross section, I,
for a polarized beam is given by
is normalized to unity the differential cross section, I,
for a polarized beam is given by

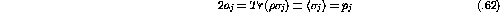
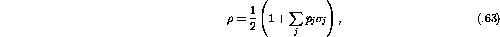
 (eqn.
(eqn. 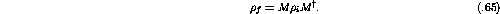

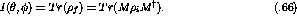 , is defined as
, is defined as
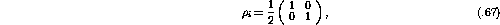
 is normalized to unity so that
is normalized to unity so that

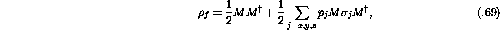
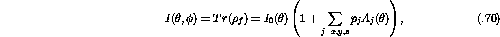
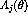 is the
is the  component of the polarization
that scattered particle would have if the beam were unpolarized
(called induced polarization), and
component of the polarization
that scattered particle would have if the beam were unpolarized
(called induced polarization), and
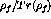 is the polarization transfer coefficient which
relates the
is the polarization transfer coefficient which
relates the 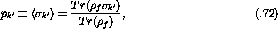 initial polarization component to the
initial polarization component to the 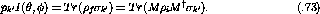 final
polarization component.
final
polarization component. 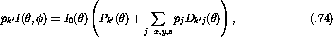 and
and
 are defined as:
are defined as:



 and
and
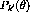 respectively, being vector quantities will change sign.
Assume the particle motion is defined as being along the z-axis, and
the scattering plane
is defined by the x- and z-axes. Under a parity transformation
the in-plane coordinates, being
defined by linear combinations of
respectively, being vector quantities will change sign.
Assume the particle motion is defined as being along the z-axis, and
the scattering plane
is defined by the x- and z-axes. Under a parity transformation
the in-plane coordinates, being
defined by linear combinations of 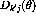 and
and 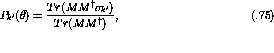 ,
will rotate
,
will rotate 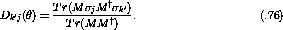 .
The y-axis will be
perpendicular to the scattering plane (in the
.
The y-axis will be
perpendicular to the scattering plane (in the 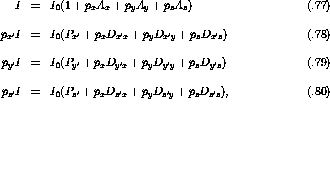 direction) and will not change sign under this
transformation. The polarization transfer coefficients which relate
polarization vectors in the scattering plane will be allowed by parity
conservation
because after the parity transformation the reaction will look exactly
the same as before. Actually, to be precise, the
reaction will look as though both the ingoing and outgoing polarization
vectors are reversed, but the linear nature of equations
direction) and will not change sign under this
transformation. The polarization transfer coefficients which relate
polarization vectors in the scattering plane will be allowed by parity
conservation
because after the parity transformation the reaction will look exactly
the same as before. Actually, to be precise, the
reaction will look as though both the ingoing and outgoing polarization
vectors are reversed, but the linear nature of equations 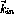 ,
, 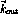 ,
, 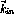 , and
, and
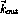 are allowed by conservation of parity. On the other hand,
if one of the polarization vectors is out of the plane (y-axis) then that
polarization vector will not change since the parity transform is closely
related to a
are allowed by conservation of parity. On the other hand,
if one of the polarization vectors is out of the plane (y-axis) then that
polarization vector will not change since the parity transform is closely
related to a 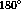 rotation around the y-axis. Because the
in-plane polarization vector changes sign, as described above, then those
coefficients must obey
rotation around the y-axis. Because the
in-plane polarization vector changes sign, as described above, then those
coefficients must obey 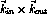 for parity to be conserved, and
so those terms must be identically zero. Finally, because the parity
transformation
doesn't affect the out-of-plane polarization vectors at all
for parity to be conserved, and
so those terms must be identically zero. Finally, because the parity
transformation
doesn't affect the out-of-plane polarization vectors at all
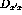 will be allowed. For similar reasons
will be allowed. For similar reasons 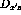 and
and 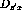 are
the only components of analyzing power and induced polarization that are
non-zero. Therefore equations
are
the only components of analyzing power and induced polarization that are
non-zero. Therefore equations 
