



Next: Figure-of-Merit Optimization
Up: Polarimeter Effective Analyzing
Previous: The Sector Method
The analyzing power of a detector is a function of
scattering angle,  , and neutron energy. Ideally the detector
should be calibrated using neutrons of known polarization at a variety of
energies covering the range of interest. This sort of calibration was the
purpose of another proposed experiment, E384, carried out at IUCF.
However, the results of that experiment are not available at the time this
thesis is being written. The primary reason that this calibration data
has not been analyzed is that it was recently determined that the
high-energy beamline
polarimeters (described in section 4.1.3) had not been
characterized for
proton energies below
, and neutron energy. Ideally the detector
should be calibrated using neutrons of known polarization at a variety of
energies covering the range of interest. This sort of calibration was the
purpose of another proposed experiment, E384, carried out at IUCF.
However, the results of that experiment are not available at the time this
thesis is being written. The primary reason that this calibration data
has not been analyzed is that it was recently determined that the
high-energy beamline
polarimeters (described in section 4.1.3) had not been
characterized for
proton energies below 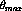 MeV. That means that the analyzing power
of the beamline polarimeters was not known at those energies so the proton
polarization and, therefore, the polarization of neutrons from a
calibrating reaction was not known. This,
in turn, meant that the neutron detector could not be calibrated with
neutrons of known polarization at those lower energies. A
measurement of the high-energy beamline polarimeters at the appropriate
energies is the focus of an experiment taking place in spring of 1997.
MeV. That means that the analyzing power
of the beamline polarimeters was not known at those energies so the proton
polarization and, therefore, the polarization of neutrons from a
calibrating reaction was not known. This,
in turn, meant that the neutron detector could not be calibrated with
neutrons of known polarization at those lower energies. A
measurement of the high-energy beamline polarimeters at the appropriate
energies is the focus of an experiment taking place in spring of 1997.
In the interim a reasonable amount of calibration data was taken at
 MeV during the E385 and E387 experiments, so, in fact, it is
possible to determine the analyzing power of the detector for 200 MeV
neutrons. Calculations of the analyzing power for free n-p scattering show
that it has a fairly flat distribution between
MeV during the E385 and E387 experiments, so, in fact, it is
possible to determine the analyzing power of the detector for 200 MeV
neutrons. Calculations of the analyzing power for free n-p scattering show
that it has a fairly flat distribution between 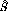 MeV, which
is the range of interest for data from the INPOL detector. Figure
MeV, which
is the range of interest for data from the INPOL detector. Figure
 shows data for an old IUCF neutron polarimeter of similar
design to the INPOL detector.
shows data for an old IUCF neutron polarimeter of similar
design to the INPOL detector.

Figure: Effective analyzing power of an old IUCF neutron polarimeter. The
square data points are values measured using neutrons from the
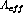 IAS reaction. The crosses are the
results of calculations based on free n-p scattering. The asterisks are
the calculated values reduced by a factor of 0.85 [Tad85].
IAS reaction. The crosses are the
results of calculations based on free n-p scattering. The asterisks are
the calculated values reduced by a factor of 0.85 [Tad85].
The data shown were taken using neutrons from the 
 IAS reaction which produced neutrons of
the same polarization as the incident protons
IAS reaction which produced neutrons of
the same polarization as the incident protons 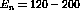 .
It appears that the data fit the shape of the free np scattering
calculations, just slightly rescaled. This phenomenon was also observed at
LAMPF for the energy range of
.
It appears that the data fit the shape of the free np scattering
calculations, just slightly rescaled. This phenomenon was also observed at
LAMPF for the energy range of  MeV [Che93]. The
conclusion then is if the detector's analyzing power is found at 200 MeV
the distribution can be assumed to be flat back to
MeV [Che93]. The
conclusion then is if the detector's analyzing power is found at 200 MeV
the distribution can be assumed to be flat back to  MeV, until a
more precise determination can be made based on improved polarimeter
calibrations.
MeV, until a
more precise determination can be made based on improved polarimeter
calibrations.
The detector calibration at  MeV was carried out using the
MeV was carried out using the
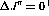 reaction. This
reaction is a pure Gamow-Teller transition. The expected value of
reaction. This
reaction is a pure Gamow-Teller transition. The expected value of  for such a transition is
for such a transition is 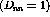 and that value has been confirmed
experimently [Rap90] at 200 MeV with an absolute uncertainty of
and that value has been confirmed
experimently [Rap90] at 200 MeV with an absolute uncertainty of
 for this particular reaction. Therefore,
for this particular reaction. Therefore,

becomes

for 200 MeV neutron detected in the INPOL polarimeter. A sample energy
spectrum from the 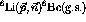 reaction is
shown in figure
reaction is
shown in figure  .
.

Figure: Sample  spectrum. The
spectrum. The
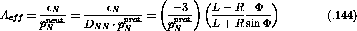 ground state is the most prominent feature. The smaller
peaks at lower neutron energy are the result of beam contamination of the
type discussed in section 4.1.3. The peak at the higher neutron
energy than the ground state is the result of
ground state is the most prominent feature. The smaller
peaks at lower neutron energy are the result of beam contamination of the
type discussed in section 4.1.3. The peak at the higher neutron
energy than the ground state is the result of 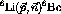 contamination
in the target.
contamination
in the target.
Another useful feature of the  target is its relatively large
cross section for the
target is its relatively large
cross section for the 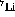 reaction
(
reaction
( mb/sr). This means that it does not take long to
gather sufficient statistics to make a statement about
mb/sr). This means that it does not take long to
gather sufficient statistics to make a statement about 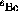 . Also,
the lack of any state near the
. Also,
the lack of any state near the 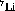 ground state means that the
resolution requirements are fairly relaxed and thicker targets can be used
to further increase the rate at which statistics are gathered.
ground state means that the
resolution requirements are fairly relaxed and thicker targets can be used
to further increase the rate at which statistics are gathered.
In practice equation  is not precisely the equation used to
calculate the effective analyzing power. Recall from section
is not precisely the equation used to
calculate the effective analyzing power. Recall from section  that
the beam polarization flips every
that
the beam polarization flips every  seconds, and that this can be
used to eliminate experimental asymmetries. By defining a quantity,
seconds, and that this can be
used to eliminate experimental asymmetries. By defining a quantity,
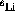 equation
equation  could
be rewritten as
could
be rewritten as

In using this equation the assumption must be made that the detectors
acceptance and efficiencies are the same for left and right scattered
particles which is, perhaps, untrue. It is possible to overcome this
difficulty without knowing the left/right asymmetries by defining the
quantity

where the superscripts indicate whether the beam is in a (+) or (-) state.
In this way any efficiency or acceptance factors associated with a given
scattering direction will cancel out assuming that the detector efficiency
is independent of the proton spin orientation. Equation  then
becomes [Tad85]
then
becomes [Tad85]

to second order in  , where
, where
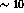 is half the difference between the polarization of
the beam in the (+) state versus the (-) state, and
is half the difference between the polarization of
the beam in the (+) state versus the (-) state, and  is the
average polarization between the two states. For the current experiment
the difference is taken to be negligible. The average proton beam
polarization for the
is the
average polarization between the two states. For the current experiment
the difference is taken to be negligible. The average proton beam
polarization for the 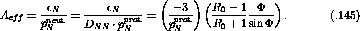 calibration runs was
calibration runs was
 .
.




Next: Figure-of-Merit Optimization
Up: Polarimeter Effective Analyzing
Previous: The Sector Method
Michael A. Lisa
Tue Apr 1 08:52:10 EST 1997
 , and neutron energy. Ideally the detector
should be calibrated using neutrons of known polarization at a variety of
energies covering the range of interest. This sort of calibration was the
purpose of another proposed experiment, E384, carried out at IUCF.
However, the results of that experiment are not available at the time this
thesis is being written. The primary reason that this calibration data
has not been analyzed is that it was recently determined that the
high-energy beamline
polarimeters (described in section 4.1.3) had not been
characterized for
proton energies below
, and neutron energy. Ideally the detector
should be calibrated using neutrons of known polarization at a variety of
energies covering the range of interest. This sort of calibration was the
purpose of another proposed experiment, E384, carried out at IUCF.
However, the results of that experiment are not available at the time this
thesis is being written. The primary reason that this calibration data
has not been analyzed is that it was recently determined that the
high-energy beamline
polarimeters (described in section 4.1.3) had not been
characterized for
proton energies below 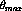 MeV. That means that the analyzing power
of the beamline polarimeters was not known at those energies so the proton
polarization and, therefore, the polarization of neutrons from a
calibrating reaction was not known. This,
in turn, meant that the neutron detector could not be calibrated with
neutrons of known polarization at those lower energies. A
measurement of the high-energy beamline polarimeters at the appropriate
energies is the focus of an experiment taking place in spring of 1997.
MeV. That means that the analyzing power
of the beamline polarimeters was not known at those energies so the proton
polarization and, therefore, the polarization of neutrons from a
calibrating reaction was not known. This,
in turn, meant that the neutron detector could not be calibrated with
neutrons of known polarization at those lower energies. A
measurement of the high-energy beamline polarimeters at the appropriate
energies is the focus of an experiment taking place in spring of 1997.
 MeV during the E385 and E387 experiments, so, in fact, it is
possible to determine the analyzing power of the detector for 200 MeV
neutrons. Calculations of the analyzing power for free n-p scattering show
that it has a fairly flat distribution between
MeV during the E385 and E387 experiments, so, in fact, it is
possible to determine the analyzing power of the detector for 200 MeV
neutrons. Calculations of the analyzing power for free n-p scattering show
that it has a fairly flat distribution between 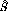 MeV, which
is the range of interest for data from the INPOL detector. Figure
MeV, which
is the range of interest for data from the INPOL detector. Figure

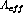 IAS reaction. The crosses are the
results of calculations based on free n-p scattering. The asterisks are
the calculated values reduced by a factor of 0.85 [
IAS reaction. The crosses are the
results of calculations based on free n-p scattering. The asterisks are
the calculated values reduced by a factor of 0.85 [
 IAS reaction which produced neutrons of
the same polarization as the incident protons
IAS reaction which produced neutrons of
the same polarization as the incident protons 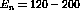 .
It appears that the data fit the shape of the free np scattering
calculations, just slightly rescaled. This phenomenon was also observed at
LAMPF for the energy range of
.
It appears that the data fit the shape of the free np scattering
calculations, just slightly rescaled. This phenomenon was also observed at
LAMPF for the energy range of  MeV [
MeV [ MeV, until a
more precise determination can be made based on improved polarimeter
calibrations.
MeV, until a
more precise determination can be made based on improved polarimeter
calibrations.
 MeV was carried out using the
MeV was carried out using the
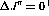 reaction. This
reaction is a pure Gamow-Teller transition. The expected value of
reaction. This
reaction is a pure Gamow-Teller transition. The expected value of  for such a transition is
for such a transition is 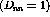 and that value has been confirmed
experimently [
and that value has been confirmed
experimently [ for this particular reaction. Therefore,
for this particular reaction. Therefore,


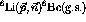 reaction is
shown in figure
reaction is
shown in figure 
 spectrum. The
spectrum. The
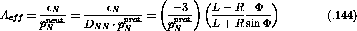 ground state is the most prominent feature. The smaller
peaks at lower neutron energy are the result of beam contamination of the
type discussed in section 4.1.3. The peak at the higher neutron
energy than the ground state is the result of
ground state is the most prominent feature. The smaller
peaks at lower neutron energy are the result of beam contamination of the
type discussed in section 4.1.3. The peak at the higher neutron
energy than the ground state is the result of 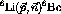 contamination
in the target.
contamination
in the target. target is its relatively large
cross section for the
target is its relatively large
cross section for the 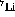 reaction
(
reaction
( mb/sr). This means that it does not take long to
gather sufficient statistics to make a statement about
mb/sr). This means that it does not take long to
gather sufficient statistics to make a statement about 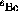 . Also,
the lack of any state near the
. Also,
the lack of any state near the 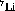 ground state means that the
resolution requirements are fairly relaxed and thicker targets can be used
to further increase the rate at which statistics are gathered.
ground state means that the
resolution requirements are fairly relaxed and thicker targets can be used
to further increase the rate at which statistics are gathered.
 seconds, and that this can be
used to eliminate experimental asymmetries. By defining a quantity,
seconds, and that this can be
used to eliminate experimental asymmetries. By defining a quantity,
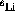 equation
equation 


 , where
, where
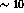 is half the difference between the polarization of
the beam in the (+) state versus the (-) state, and
is half the difference between the polarization of
the beam in the (+) state versus the (-) state, and  is the
average polarization between the two states. For the current experiment
the difference is taken to be negligible. The average proton beam
polarization for the
is the
average polarization between the two states. For the current experiment
the difference is taken to be negligible. The average proton beam
polarization for the  calibration runs was
calibration runs was
 .
.