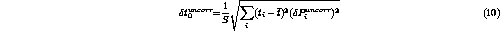
The uncertainty in the mean, specified in Equation 3, arises from uncorrelated as well as correlated uncertainties in the ADC sums (due again to white and ``filtered'' noise). These may be expressed as [9]
where  is just
is just 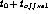 , and
, and 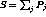 .
The overall uncertainty is then estimated as
.
The overall uncertainty is then estimated as
Values of the uncorrelated and correlated noise for use in Equations10 and 11 are estimated as
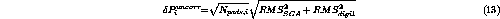
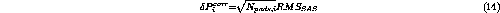
where 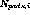 is the number of pads that contributed nonzero ADC values
to the
is the number of pads that contributed nonzero ADC values
to the 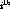 time bucket of the time projection.
time bucket of the time projection.
(Of course, since in calculating the mean with finite sums instead
of integrals in Equation 3, we have an additional
error 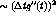 , where
, where 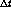 is the width
of a time bucket, and the shaper response g(t) is given
in 4. We ignore this here, as
the effect of time bucket width,
when
is the width
of a time bucket, and the shaper response g(t) is given
in 4. We ignore this here, as
the effect of time bucket width,
when 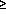 512 buckets are used, has been seen to be
small [11].
512 buckets are used, has been seen to be
small [11].
As with the uncertainty along the padrow, Equation 12
estimates the uncertainty in time (z-position) only for  =0
tracks. A non-zero crossing angle will degrade the spatial resolution
in z. We follow Equation 9 in parametrizing the
time resolution.
=0
tracks. A non-zero crossing angle will degrade the spatial resolution
in z. We follow Equation 9 in parametrizing the
time resolution.
As with the resolution along the padrow, the constants 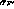 and
and 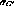 must be determined empirically. See
Section 6.3.2.
must be determined empirically. See
Section 6.3.2.
Again, for the uncertainty in the time (z) direction, only an estimate
of the first term in Equation 15 is provided by
the cluster/hitfinder and stored in TPHIT.DZ. Tracking software,
which has a hypothesis of the crossing angle  , must update
this uncertainty.
, must update
this uncertainty.