 ***some pump/probe curves***
***some pump/probe curves***
State specific energy transfer studies are a fundamental means of investigating collisions. Our goal has been to develop models based on physical parameters and to subject these models to rigorous experimental tests. This has been historically difficult because of the fundamental complexity of the problem and the nature of the required experiments. To date this work has been in the region ~100 - 500 K, and, as expected, the observed phenomena can be characterized by semi-classical models and theory.
We have chosen to focus on symmetric tops and similar molecules (e. g. slightly asymmetric rotors and linear molecules) and to make observations as a function of temperature. Because collisional phenomena are so dependent on collision energy, experimental observables are often steep functions of temperature. As a result, these temperature dependencies provide stringent tests of the physical basis of the parameters which characterize the mathematical models used to describe rotational energy transfer (RET).
Here we will briefly describe some of our most recent results. These include:
We have previously shown for CH3F - CH3F
collisions within the thermally populated rotational manifold that for
![]() K
K
![]() 0 RET the molecular populations
transferred by collisions to other K states can be described (independent of
initial or final (J, K) state) by a Boltzmann distribution at 300 K
(422).
In these time resolved double resonance experiments,
molecules were placed in a specific rotational state of the
0 RET the molecular populations
transferred by collisions to other K states can be described (independent of
initial or final (J, K) state) by a Boltzmann distribution at 300 K
(422).
In these time resolved double resonance experiments,
molecules were placed in a specific rotational state of the
![]() 3 vibrational state
by a Q-switched CO2 laser and the collision induced RET was
monitored by a mm/submm probe. The experimental signature for the
3 vibrational state
by a Q-switched CO2 laser and the collision induced RET was
monitored by a mm/submm probe. The experimental signature for the
![]() K
K
![]() 0 RET was a time dependence of
the transferred population which was independent of pumped or probed (J, K)
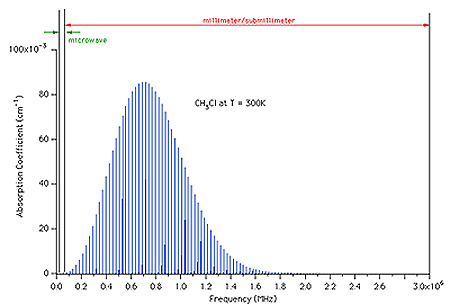
state. However, in a subsequent study of CH3Cl it was found that
the experimental signature, two examples of which are shown in Fig. C.3.c-1,
was more complex and a function of both the K of the probed state and the
energy of the pumped state. In the CH3Cl experiments the 9P(26)
CO2 laser line pumps the J = 4, K = 4 state (Er ~ 80
cm-1) in
0 RET was a time dependence of
the transferred population which was independent of pumped or probed (J, K)
state. However, in a subsequent study of CH3Cl it was found that
the experimental signature, two examples of which are shown in Fig. C.3.c-1,
was more complex and a function of both the K of the probed state and the
energy of the pumped state. In the CH3Cl experiments the 9P(26)
CO2 laser line pumps the J = 4, K = 4 state (Er ~ 80
cm-1) in
![]() 6 and the 9R(12) CO2 laser line pumps the J = 12, K = 6
state (Er ~ 280 cm-1).
6 and the 9R(12) CO2 laser line pumps the J = 12, K = 6
state (Er ~ 280 cm-1).
 |
While it would have been possible to describe the CH3Cl results with a variety of complex, multiparameter models, we found that it is possible to maintain the thermal model of CH3F with the modification that the initial temperature of the Boltzmann distribution corresponds to the energy of the pumped state and that this temperature subsequently relaxes to the translational temperature (422).
In this context, the data in the 300 K row of the figure are straightforward to understand. For the lower energy 9P26 pump, the initial energy transfer favors the low energy states shown which are more strongly populated by a colder Boltzmann distribution over higher energy states. Subsequent relaxation to the translational temperature produces a distinct "early time feature" for the low energy states which is observable in the figure. For the higher energy 9R12 pump, the initial rotational temperature is close to the translational temperature and the subsequent relaxation is not visually obvious in the figure.
Additionally, this model makes straightforward predictions of the temperature dependence of the observed phenomena. For example, as the ambient temperature is reduced toward the temperature of the initial Boltzmann distribution, the early time features which result from the difference between the kinetic and initial rotational temperature should be reduced. Figure C.3.c-1 shows the quantitative success of the model. For the low energy pump, where the effect is largest, it can be seen that the change in the time response with temperature is accurately predicted by this model, without the need for any additional temperature dependent parameters.
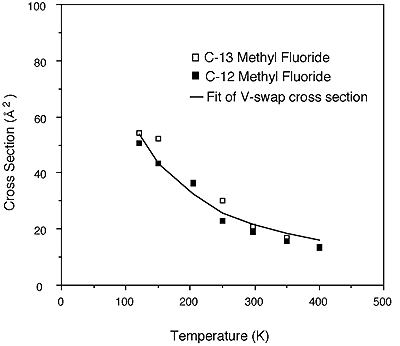
In another experiment we have shown that the temperature dependence of the fast vibrational swapping which effectively moves population from one symmetry species to the other can be quantitatively accounted for by means of an Anderson like semiclassical process which depends on the fourth power of the dipole derivative matrix element (445). While the underlying physics is more complex and less intuitive, the figure shows the basic success of the theory. The line calculated from theory in the figure uses no adjustable parameters, but rather a dipole derivative calculated from infrared line strengths. In fact, because of the dependence of the rate on the fourth power of this parameter, the experimental data are within the error limits propagated from the parameter used.
 |