
| email: | dsivakoff(at)stat[dot]osu.edu |
| office: | 440A Cockins Hall |
Research
Interacting Particle Systems and Cellular Automata
An interacting particle system is a network of dynamic units in which the state of each vertex evolves stochastically in continuous time according to a local rule. Cellular automata are the deterministic, discrete time analogues of interacting particle systems. Both paradigms are commonly used as models for discrete, spatial processes, and we are typically interested in the emergence of global structure or long-time behavior as these systems evolve from a disordered initial state. Classically, the underlying topology is taken to be a lattice (such as ℤd) or an infinite tree, while more recently, researchers have focused on more heterogeneous stuctures, such as random graphs. I have studied a variety of systems, which include models for epidemics [11, 25], tumor formation [29], coupled oscillators [15, 17, 26, 30], opinion spreading [4], ferromagnetic spin systems [16], and systems of ballistic and annihilating particles [15, 18, 23, 24, 28, 32]. I have also worked with an interdisciplinary team on an empirical study of how ``official'' and ``social'' information sources influence knowledge and opinions [20, 21].
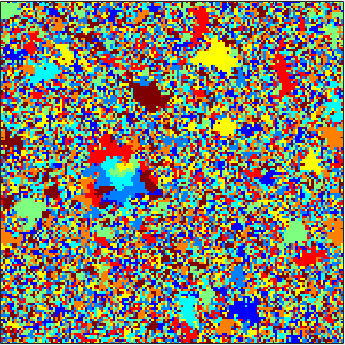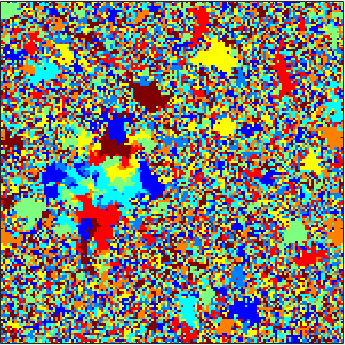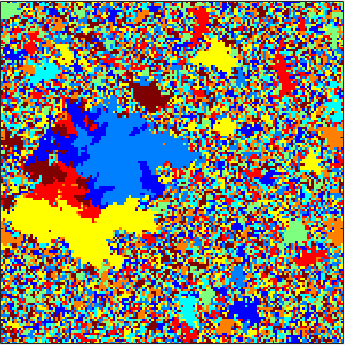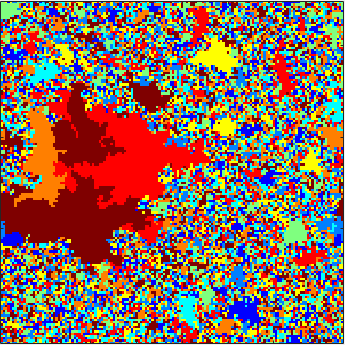
The first animation to the left depicts the 8-color cyclic cellular automaton [15] on a uniform minimal spanning tree of the 150 x 150 discrete torus. Most vertices cease to be active early on, while rare regions of activity appear to nucleate and eventually force the entire graph to fluctuate.
An interacting particle system is a network of dynamic units in which the state of each vertex evolves stochastically in continuous time according to a local rule. Cellular automata are the deterministic, discrete time analogues of interacting particle systems. Both paradigms are commonly used as models for discrete, spatial processes, and we are typically interested in the emergence of global structure or long-time behavior as these systems evolve from a disordered initial state. Classically, the underlying topology is taken to be a lattice (such as ℤd) or an infinite tree, while more recently, researchers have focused on more heterogeneous stuctures, such as random graphs. I have studied a variety of systems, which include models for epidemics [11, 25], tumor formation [29], coupled oscillators [15, 17, 26, 30], opinion spreading [4], ferromagnetic spin systems [16], and systems of ballistic and annihilating particles [15, 18, 23, 24, 28, 32]. I have also worked with an interdisciplinary team on an empirical study of how ``official'' and ``social'' information sources influence knowledge and opinions [20, 21].
The first animation to the left depicts the 8-color cyclic cellular automaton [15] on a uniform minimal spanning tree of the 150 x 150 discrete torus. Most vertices cease to be active early on, while rare regions of activity appear to nucleate and eventually force the entire graph to fluctuate.

Neighborhood growth models
This is a class of growth models in which an occupied subset of the vertices of a graph grows iteratively by including vertices whose neighborhoods contain certain patterns of occupied vertices. The simplest example is a threshold growth model called bootstrap percolation, which has a long history in both physics and mathematics. This model has received the most attention on lattices and trees with nearest neighbor connectivity. My collaborators and I initiated the study of bootstrap percolation [8] and more general neighborhood growth models [14] on subsets of the lattice with connectivity of the Hamming graph, and more recently with large (but finite) +-shaped neighborhoods [31]. In the Hamming graph setting, we observe vastly different behavior than in the local-connectivity case, such as gradual phase transitions. In the case of +-shaped neighborhoods, we observe branching process-like nucleation that leads to eventual 2-dimensional nucleation (second image on left).
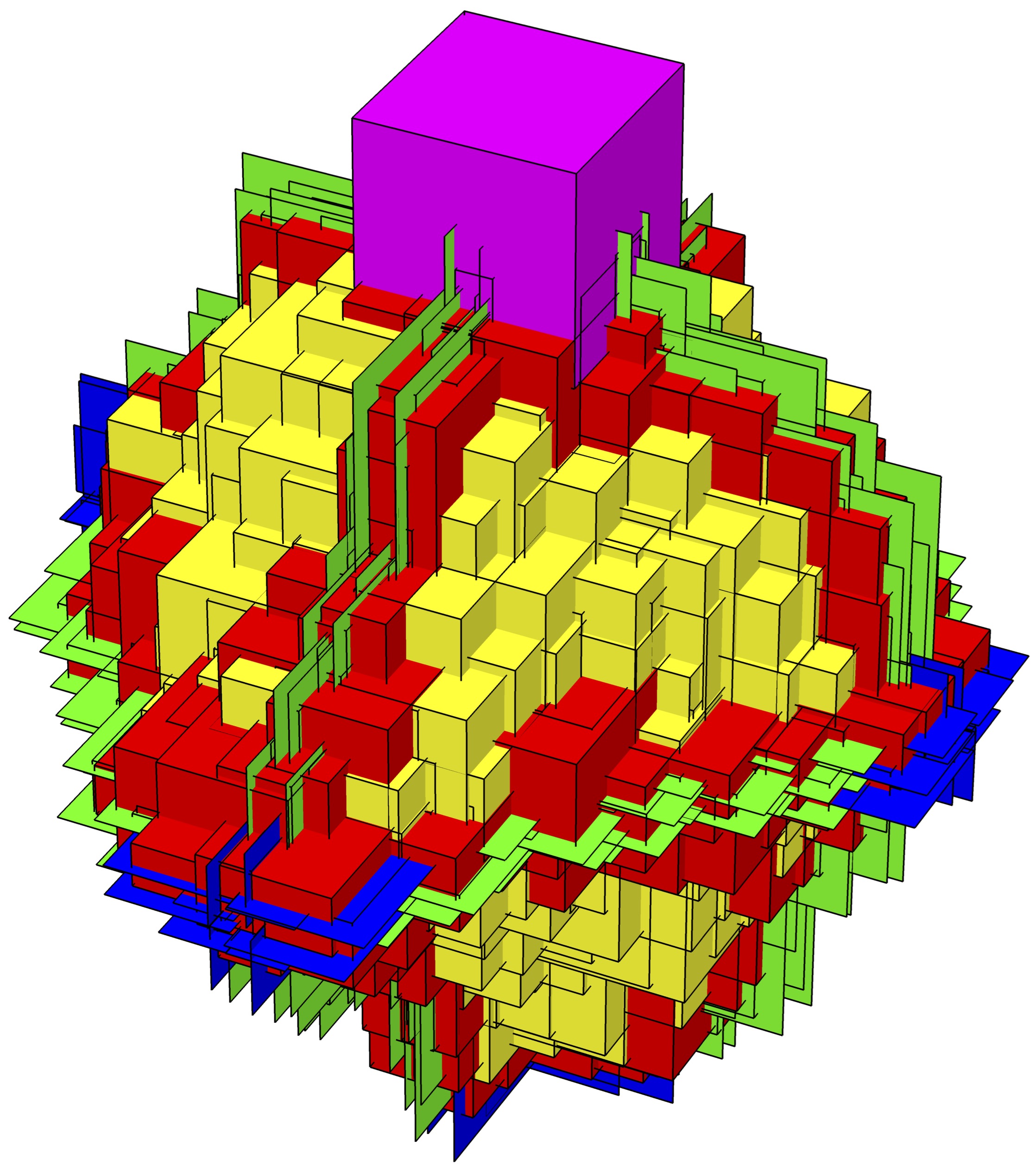
I have also
investigated bootstrap percolation on graphs with overlapping community structure [12,19], and observed that sharp,
gradual and hybrid phase transitions are possible, depending on scaling between the intra- and inter-community
connectivity and on the parity of the threshold parameter.
The effects of heterogeneity in the growth rule or environment remain poorly understood, and I recently analyzed a bootstrap percolation model in the presence of randomly placed obstacles [22]. In three dimensions and with occupation threshold 3, we use the technology of oriented surfaces to identify a blocking structure ("stegosaurus" image to the left courtesy of A. Holroyd), which prevents occupation of the origin when the density of obstacles exceeds the cube of the density of occupied sites.
I gratefully acknowledge the NSF and the Simons Foundation for supporting my research.
The effects of heterogeneity in the growth rule or environment remain poorly understood, and I recently analyzed a bootstrap percolation model in the presence of randomly placed obstacles [22]. In three dimensions and with occupation threshold 3, we use the technology of oriented surfaces to identify a blocking structure ("stegosaurus" image to the left courtesy of A. Holroyd), which prevents occupation of the origin when the density of obstacles exceeds the cube of the density of occupied sites.
I gratefully acknowledge the NSF and the Simons Foundation for supporting my research.
Papers
-
Preprints and Submitted Manuscripts
- J. Gravner and D. Sivakoff. Competing deterministic growth models in two dimensions. 2024 [arXiv].
- S. Ahn, M. Junge, H. Lyu, L. Reeves, J. Richey and D. Sivakoff. Diffusion-limited annihilating-coalescing systems. 2023 [arXiv].
- D. Blanquicett, J. Gravner, D. Sivakoff and L. Wilson. Two-dimensional supercritical growth dynamics with one-dimensional nucleation. 2023 [arXiv].
- A. Aguirre, H. Lyu and D. Sivakoff. Phase transition in one-dimensional excitable media with variable interaction range. Updated 2024 [arXiv].
- J. Foo, E.B. Gunnarsson, K. Leder and D. Sivakoff. Dynamics of advantageous mutant spread in spatial death-birth and birth-death Moran models. Communications on Applied Mathematics and Computation, 2024; 6(1), 576-604. [Journal].
- T. Johnson, M. Junge, H. Lyu and D. Sivakoff. Particle density in diffusion-limited annihilating systems. Annals of Probability, 2023; 51(6), 2301-44. [arXiv] [Journal].
- H. Lyu, F. Memoli and D. Sivakoff. Sampling random graph homomorphisms and applications to network data analysis. Journal of Machine Learning Research, 2023; 24 (9), 1-79. [Journal].
- J. Bello and D. Sivakoff. Cyclic Cellular Automata and Greenberg-Hastings Models on Regular Trees. Annals of Applied Probability, 2023; 33(4), 3080-97. [arXiv] [Journal].
- S. Chatterjee, D. Sivakoff and M. Wascher. The effect of avoiding known infected neighbors on the persistence of a recurring infection process. Electronic Journal of Probability, 2022; 27, 1-40. [Journal].
- I. Cristali, Y. Jiang, M. Junge, R. Kassem, D. Sivakoff and G. York. Two-type annihilating systems on the complete and star graph. Stochastic Processes and their Applications, 2021; 139, 321-342. [Journal].
- M. Damron, H. Lyu and D. Sivakoff. Stretched exponential decay for subcritical parking times on ℤd. Random Structures & Algorithms, 2021; 59(2), 143-54. [Journal].
- J. Gravner, A. E. Holroyd and D. Sivakoff. Polluted bootstrap percolation in three dimensions. Annals of Applied Probability, 2021; 31(1), 218-246. [Journal].
- E. Assaf, R.M. Bond, S.J. Cranmer, E.E. Kaizar, L.R. Santoro, S. Shikano and D.J. Sivakoff. Understanding the Relationship Between Official and Social Information About Infectious Disease: Experimental Analysis. Journal of medical Internet research, 2021; 23(11), e25287. [Journal].
- L.R. Santoro, E. Assaf, R.M. Bond, S.J. Cranmer, E.E. Kaizar and D.J. Sivakoff. Exploring the direct and indirect effects of elite influence on public opinion. PloS one, 2021; 16(11), e0257335. [Journal].
- J. Gravner and D. Sivakoff. Bootstrap percolation on the product of the two-dimensional lattice with a Hamming square. Annals of Applied Probability, 2020; 30(1), 145-174. [Journal].
- M. Damron, J. Gravner, M. Junge, H. Lyu and D. Sivakoff. Parking on transitive unimodular graphs. Annals of Applied Probability, 2019; 29(4), 2089-2113. [Journal].
- H. Lyu and D. Sivakoff. Persistence of sums of correlated increments and clustering in cellular automata. Stochastic Processes and their Applications, 2019; 129(4), 1132-1152. [Journal].
- M. Damron, L. Petrov and D. Sivakoff. Coarsening model on ℤd with biased zero-energy flips and an exponential large deviation bound for ASEP. Communications in Mathematical Physics, 2018; 362(1), 185-217. [Journal].
- J. Gravner, H. Lyu and D. Sivakoff. Limiting behavior of 3-color excitable media on arbitrary graphs. Annals of Applied Probability, 2018; 28(6), 3324-3357. [journal].
- J. Gravner, D. Sivakoff and E. Slivken. Neighborhood growth dynamics on the Hamming plane. Electronic Journal of Combinatorics, 2017; 24(4) #P4.29, 1-55. [journal].
- J. Gravner and D. Sivakoff. Nucleation scaling in jigsaw percolation. Annals of Applied Probability, 2017; 27(1), 395-438. [journal].
- J. Gravner and D. Sivakoff. Bootstrap percolation on products of cycles and complete graphs. Electronic Journal of Probability, 2017; 22(29), 20pp. [journal].
- D. Sivakoff. Contact process on a graph with communities. ALEA: Latin American Journal of Probability and Statistics, 2017; 14, 9-31. [journal].
- C. D. Brummitt, S. Chatterjee, P. S. Dey and D. Sivakoff. Jigsaw percolation: What social networks can collaboratively solve a puzzle? Annals of Applied Probability, 2015; 25(4), 2013-2038. [journal].
- M. D. Ryser, K. McGoff, D. P. Herzog, D. Sivakoff and E. R. Myers. Impact of coverage-dependent marginal costs on optimal HPV vaccination strategies. Epidemics, June 2015; 11, 32–47. [journal].
- J. Gravner, C. Hoffman, J. Pfeiffer and D. Sivakoff. Bootstrap percolation on the Hamming torus. Annals of Applied Probability, 2015; 25(1), 287-323. [journal].
- I. Matic and D. Sivakoff. Excited deterministic walk in a random environment. Electronic Journal of Probability, 2015; 20(44), 19pp. [journal].
- S. Magura, V. Pong, R. Durrett and D. Sivakoff. Two evolving social network models. ALEA: Latin American Journal of Probability and Statistics, 2015; 12(2), 699-715. [journal]
- D. Sivakoff. Site percolation on the d-dimensional Hamming torus. Combinatorics, Probability and Computing, 2014; 23(02), 290-315. [journal].
- R. Durrett, J. P. Gleeson, A. L. Lloyd, P. J. Mucha, F. Shi, D. Sivakoff, J. E. S. Socolar and C. Varghese. Graph fission in an evolving voter model. Proceedings of the National Academy of Science, 2012; 109(10), 3682-3687. [journal].
- S. Parthasarathy, D. Sivakoff, M. Tian and Y. Wang. A quest to unravel the metric structure behind perturbed networks. Proceedings of Symposium on Computational Geometry (SoCG), 2017. [arXiv].
- Y. Wang, A. Chakrabarti, D. Sivakoff and S. Parthasarathy. Hierarchical change point detection on dynamic networks. Proceedings of ACM WebSci, 2017. [arXiv].
- Y. Wang, A. Chakrabarti, D. Sivakoff and S. Parthasarathy. Fast change point detection on dynamic social networks. Proceedings of International Joint Conference on Artificial Intelligence (IJCAI), 2017. [arXiv].
Journal Articles
Conference Proceedings
Teaching
I am teaching Stat 6201 (Mathematical Statistics) and Math 6251 (Probability I) during Autumn 2024. Course webpages are maintained on Carmen.
Previously, I have taught:
At OSU:
Stochastic Processes (Stat 7540) in Spring 2019, 2023, 2024
Probability II (Math 6252) in Spring 2019, 2020, 2022, 2023, 2024
Real Analysis I (Math 6211) in Autumn 2017
Probability (Stat 7201) in Autumn 2013, 2015, 2016, 2018, 2019, 2021, 2022
Probability (Math 4530) in Autumn 2016 (2 sections), 2019, 2021
Probability I (Math 6251) in Autumn 2015
Real Analysis II (Math 6212) in Spring 2015
Mathematical Statistics I (Stat 4201) in Spring 2014, Autumn 2020 (Distance Learning)
At Duke:
Probability (Math 135) in Fall 2011, Spring 2012
Advanced Calculus (Math 431) in Spring 2013
Applied Stochastic Processes (Math 541) in Fall 2012
Stochastic Networks Graduate Mini-Course (Math 690) in Fall 2012
Students
I have advised a number of students from both the Mathematics and Statistics departments at OSU.
Ph.D. students:
Xingyi Li (Mathematics, continuing)
Andrew Heeszel (Statistics, continuing)
Zihao Fang (Mathematics, continuing)
Nikolas Henderson (Mathematics, 2024)
Amartya Ghosh (Statistics, 2022)
Jason Bello (Mathematics, 2021)
Matthew Wascher (Statistics, 2020)
Hanbaek Lyu (Mathematics, 2018)
Wendy Ran Wei (Statistics, 2016; coadvised by Elizabeth Stasny)
M.S. students:
Ryan Brune (Statistics, 2022)
Samuel Mossing (Mathematics, 2019)