When we are on the surface of the earth, gravity is a constant force, which produces a 9.8 $\rm {m/s}^2$ acceleration towards the ground. The coding activities Lunar Descent and Bellicose Birds explore this situation. In general, gravity is a force that depends on the distance between objects. Here is the formula: $$F_{grav} = \frac{G M m }{r^2}$$
where $M$ is the mass of one object (usually the larger object), $m$ is the mass of another object (usually the smaller object), $r$ is the distance between the centers of those objects, and $G$ is a constant related to the strength of the gravitational force (not to be confused with $g = 9.8 \, \rm{m/s}^2$ which is a lowercase $g$)
When we are on the surface of the earth, even if we climb to the top of a mountain, the distance between us and the center of the earth changes by an amount that is small compared to radius of the earth itself. As a result, a gravity measurement on the top of that mountain would give something very close to 9.8 $\rm{m/s}^2$.
This being the case, you might wonder how we even figured out that the force of gravity gets weaker according to the square of the distance between objects (like in the equation for $F_{grav}$ above). This coding activity will help explain how we arrived at that knowledge.
Disclaimer: You need to have finished Accelerate the Blob to work on this exercise!. It is also good if you have finished the Planetoids coding activity. You may also want to check out the code for Force the Blob which is like accelerate the blob but with the arrow keys controlling the force instead of the acceleration.
If for some reason the link doesn't work you can click here to use the interactive
Play around with it. Click and drag the mouse to launch the object in various directions!
Here is the draw function for the zero-gravity (a.k.a. zero force) slingshot interactive:
function draw(){
// Update velocities
vx += deltaVx;
vy += deltaVy;
// Update location
x += vx*dt;
y += vy*dt;
// velocity is unchanged if there are no forces
deltaVx = 0;
deltaVy = 0;
// This will clear the screen and re-draw it
display();
// Add more graphics here before the end of draw()
drawBlob(x,y,vx,vy,0,0);
} // end draw()
As you know, the draw function is always where we put the physics of the problem. We put the graphics in subroutines like display(); and drawBlob.
Where is the physics here? What is the physics? Are there any forces? Acceleration? How does this compare to the Planetoids code? Or the code from Accelerate the blob?
Play around with the zero-gravity slingshot interactive Look closely at the path of the object. Is there any way to make the trajectory curved just by clicking and dragging the mouse?
Complete this sentence:
An object in motion will continue moving in a __________ if there are no forces acting on it
We are going to model an object (comet, planet, asteroid, etc.) in the solar system which means that we are going to need a sun. Once we have a sun we can add gravity.
Step 4a. Add the position of the sun
Before we can add the sun we need to add variables to the beginning of the code that specify where the sun will be. It turns out the middle of the sketch is at (350,250) so we'll put the sun there:
x_sun = 375; y_sun = 250;
Add this to the beginning of the code! Don't put it in the draw function or it won't work!
Step 4b. Add a yellow circle for the sun
Next add the drawSun command to put a silly yellow circle at the center of the sketch.
Put this after the display(); function but before the end of the draw() function:
drawSun(x_sun,y_sun,0,0,0,0);
At this point your code should behave like this
Step 4c. Add variables for the mass of the sun and the gravitational constant
Now add variables for the mass of the sun and the strength of the gravitational force to near the beginning of the program (anywhere before the draw function)
M = 1000; G = 100;
You may have noticed that these are not the correct values for the mass of the sun or the strength of gravity in real life, and that is true. If you'd rather use the correct values and wait a year for the simulation to let the earth move around the sun you are welcome to do that (actully don't do that -- a year is too long to wait for a simulation to finish!).
Step 4d. Calculate the distance and the angle between the object and the sun
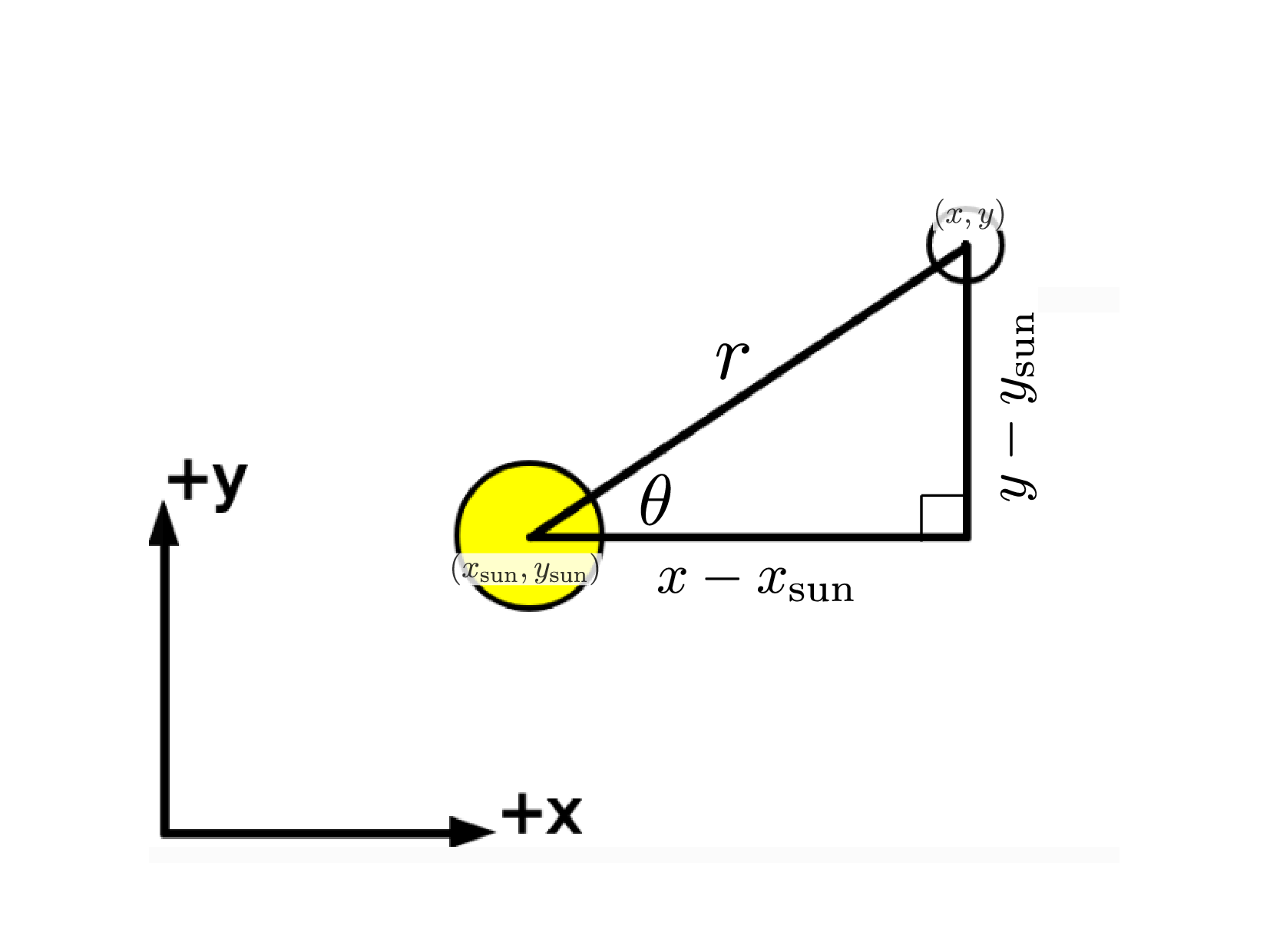
In order to calculate the strength of the gravitational force we need to know the distance between the object at ($x,y$) and the sun at ($x_{\rm sun}, y_{\rm sun}$). Here is an image of how to think about this:

If you imagine that the line between the sun at ($x_{\rm sun},y_{\rm sun}$) and the object at ($x,y$) is the hypotenuse of a right triangle you would conclude that distance between them is this: $$r = \sqrt{(x - x_{\rm sun})^2 + (y - y_{\rm sun})^2}$$
In computer world we have to write this in a funny way because ^2 does not actually take the square of the number. Here is how this expression looks in computer world:
r = sqrt((x - x_sun)*(x - x_sun) + (y - y_sun)*(y - y_sun));
We also need to figure out the angle that the line between the objects makes with the $x$ axis. We can figure this out with an inverse tangent: $$\theta = \tan^{-1} \left( \frac{y - y_{\rm sun} }{x - x_{\rm sun}}\right)$$
This works great except that it might give the wrong answer when $y - y_{\rm sun} < 0$ and $x - x_{\rm sun} < 0$, in which case the object would be below and to the left of the sun (instead of above and to the right as in the figure above). To account for this we use the atan2 function which looks like this:
theta = atan2(y - y_sun, x - x_sun);
As you can see there are two arguments to this function. If $y - y_{\rm sun} > 0$ and $x - x_{\rm sun} > 0$ the code above will give the same result as theta = atan((y - y_sun)/(x - x_sun)); but in general you will want to use the atan2 function.
Paste this code in the middle of the draw function but before the display function!
Step 4e. Calculate the magnitude and components of the gravitational force
As mentioned earlier, the magnitude of the gravitational force is this: $$F_{grav} = \frac{G M m}{r^2}$$
We need to put this into the code. Here is the right way to put this into the code:
Fgrav = G*M*mass/(r*r);
Notice that we have used r*r instead of r^2 because, for reasons known only to computer scientists, ^2 doesn't actually square anything like you might expect.
Now we have to figure out the components of the force like we had to for the planetoids game Here is a diagram that should help:
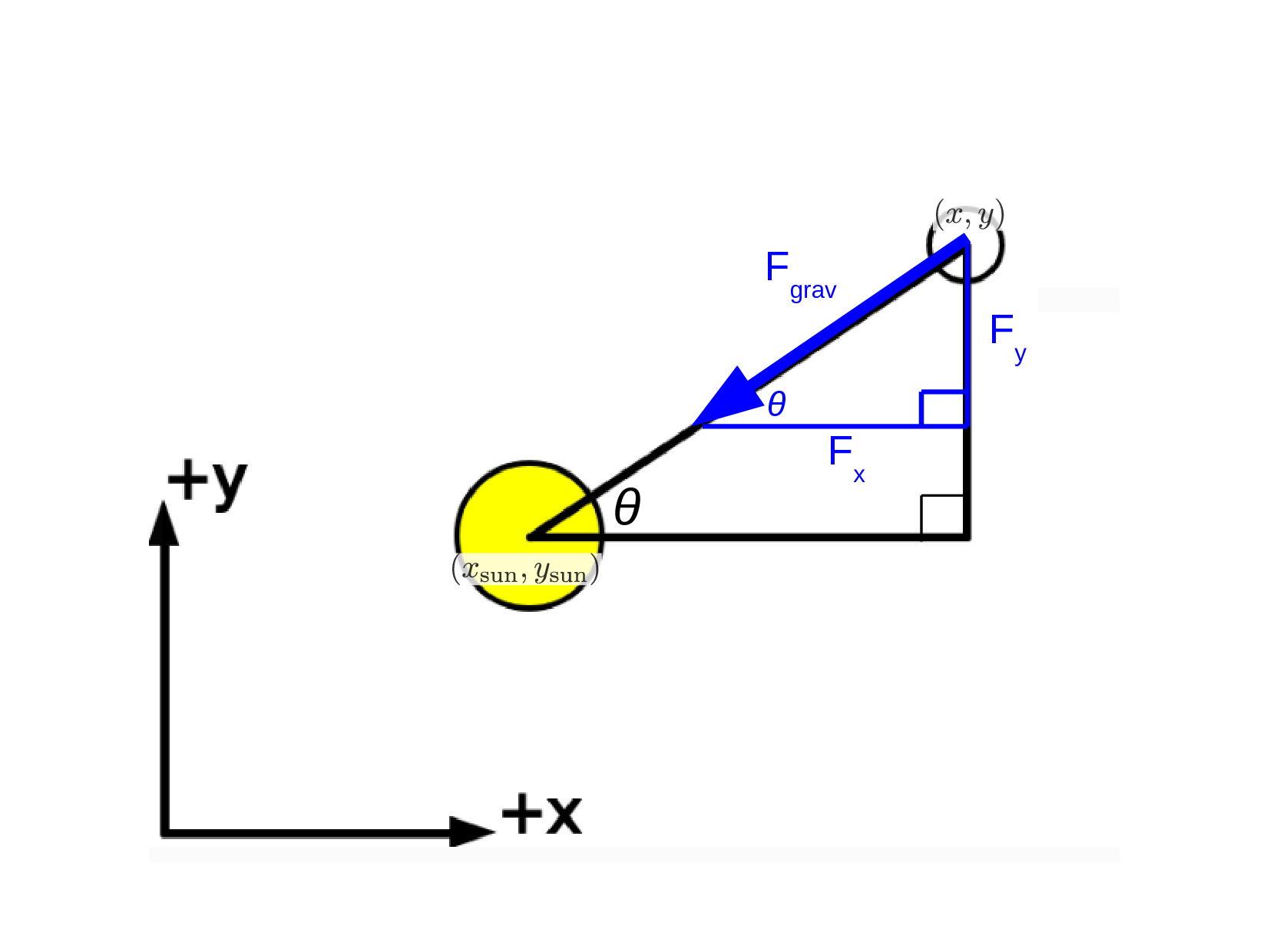
The interesting thing about this diagram is that it looks a lot like the diagram we drew for the ship in Planetoids if the ship was at the location of the sun and pointing at an angle $\theta$ above the $x$ axis. In that case we had this for the components: $$F_x = F_{\rm thrust} \cos \theta $$ $$F_y = F_{\rm thrust} \sin \theta $$
where $F_{\rm thrust}$ is the magnitude of the force. Here we have a similar situation except that the force is acting on the object out at ($x,y$) and the force is pushing in the direction opposite to the line at an angle $\theta$ with the $x$ axis (which is a lot like the reverse thrusters in Planetoids which apply a force opposite to the direction the ship is pointing -- we just added minus signs to the components to reverse the direction of the thrust).
If you combine these ideas together you get this for the components of the force on the object: $$F_x = -F_{\rm grav} \cos \theta$$ $$F_y = -F_{\rm grav} \sin \theta$$
In computer world this is just:
Fx = -Fgrav*cos(theta); Fy = -Fgrav*sin(theta);
It's nice that something looks the same in computer world as it does in math world!
Make sure to put the lines of code in this step after the expression for r and theta from Step 4d.
Step 4f. Calculate the acceleration and change in velocity
Last part of step 4! Now that we know the force we can figure out the acceleration in the x and y directions: $$a_x = \frac{F_x}{m}$$ $$a_y = \frac{F_y}{m}$$
With this we can calculate how much the velocities in the x and y directions ($v_x, v_y$) have changed during the time interval ($\Delta t$ = dt)
$$\Delta v_x = a_x \Delta t$$
$$\Delta v_y = a_y \Delta t$$
We can combine these together with this code:
deltaVx = (Fx/mass)*dt; // = ax*dt; deltaVy = (Fy/mass)*dt; // = ay*dt;
The // = ax*dt; is just a comment that does not affect the operation of the code. You can copy the code by clicking this button:
Paste this into the code after the code from Step 4e. Once you do this your code should behave like this
Optional: If you wish you can safely delete these lines of code:
// velocity is unchanged if there are no forces
deltaVx = 0;
deltaVy = 0;
These lines of code are unneccessary now because deltaVx and deltaVy are determined from the force of gravity. You can leave them in or you can delete them. It shouldn't make a difference to the operation of the program.
Now that you have gravity in your code, you can show the force vector by changing the drawBlob(x,y,vx,vy,0,0); command to this:
drawBlob(x,y,vx,vy,Fx,Fy);
Once you do this your code should behave like this
The Earth (or Jupiter or any object in the solar system) does exert a force on the sun, it's just that the sun is so massive that it barely moves in response. To show the force on the sun from the object, you can modify the code that displays the sun to this:
drawSun(x_sun,y_sun,0,0,-Fx,-Fy);
You can appreciate that the minus signs there means that the force is the same as the force that the sun exerts on the object, but in the opposite direction. The above is how a computer thinks about Newton's third law of motion. If you make this change your code should behave like this
Later if you want to include the motion of the sun there is a challenge to do this. For now let's just assume that it doesn't move and focus on the motion of the object.
Play around with the code, launching the object at different angles and different speeds. Play around, but try to avoid letting the object get too close to the sun!
Here is the question: Does the trajectory of the object typically follow the same path orbit after orbit? Or does it take a different path each time? Again, try to avoid getting the object too close to the sun. A little warning will pop up if you get too close.
Around the time that Sir Issac Newton started his work, it was generally known that the planets followed elliptical orbits (thanks to Kepler's observations) but if there was a force of gravity, people weren't sure how its strength depended on the distance between objects.
Let's imagine a different law of gravity: $$F_{\rm grav} = \frac{G M m}{r^n}$$
where $n$ is some power. We all know that the correct answer is $n = 2$ but what happens when $n$ is some other value like $n = 1.5$ or $n = 2.5$?
Let's add a variable to the beginning of the code:
npower = 2.0;
Then let's change the force law to this:
Fgrav = G*M*mass/pow(r,npower);
What happens now? Do the trajectories follow a closed path or do they make all kinds of interesting shapes?
Advice: You can use the slingshot to launch the object in various directions or velocities or you can just set vx = 0; and vy = 20; and change npower from 1.5 to 2.5 to see the effect of changing the power.
In the 1600s Sir Issac Newton invented calculus in order to prove that the elliptical orbits of the planets could be explained by a force that becomes weaker according to $1/r^2$. The complicated but elegant result that would fill a few blackboards with equations is one of the most heroic moments in math and physics.
If Newton had a computer he never would have needed to invent calculus! He could have thought about the geometry and trigonometry of the problem and let the computer figure out that you only get ellipical orbits when $n = 2$. This is the great part about computers! You don't have to be Sir Issac Newton to figure out useful things.
Researchers today still try to test whether the $1/r^2$ force of gravity remains valid on both very small and very large scales. If it turns out that gravity does not obey $1/r^2$ on some scale this is a sign that there are multiple dimensions beyond the three spatial dimensions that we are familiar with (which could tell us something really exciting about string theory or cosmology!). The men and women who perform this research do things very similar to the coding activity you just did. They perform simulations of what would happen if the force of gravity were different and they compare it to a simulation where the force of gravity is the usual $1/r^2$. Maybe someday this will be the research that you do!
Add variables for the velocity of the sun (vx_sun, vy_sun) and the change in velocity of the sun (deltaVx_sun, deltaVy_sun). Modify the code so that there is a velocity update and a location update for the sun. Model this after the velocity update and location update for the object and model the code that determines deltaVx_sun and deltaVy_sun after the part of the code that determines those values from the force of gravity on the object.