



Next: Density Dependent Mass
Up: Corrections to RPA
Previous: Distorted Wave Impulse
The relativistic treatment of the quasifree nucleon-nucleus scattering has
been described in [SRM86], [HoI86], [HoM88], [HiD94]
and in
particular for charge exchange reactions in [HoP93]. The method
generally employed uses a relativistic random phase approximation to the
Walecka model. In the Walecka model the nn interaction is mediated by the
exchange of isoscalar scalar 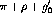 and vector
and vector 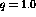 mesons, and
in the mean-field approximation these meson fields are replaced by their
classical expectation value.
In the mean-field approximation strong scalar
and vector mean-fields will cause large shifts in the in-medium mass and
energy of nucleons in the nucleons:
mesons, and
in the mean-field approximation these meson fields are replaced by their
classical expectation value.
In the mean-field approximation strong scalar
and vector mean-fields will cause large shifts in the in-medium mass and
energy of nucleons in the nucleons:

where 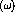 is the mean scalar field and
is the mean scalar field and  is the
free(in-medium) nucleon mass.
is the
free(in-medium) nucleon mass.
The modified mass of the nucleon is in
itself a reasonable explanation for the lack of enhancement because the
reduced value of the nucleon mass should have a significant effect on
the longitudinal spin-isospin response. An RPA calculation of the pion
dimesic function [DaP91] gives the effective 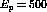 coupling constant
in the nuclear medium as [HoP93]
coupling constant
in the nuclear medium as [HoP93]

If the pion coupling constant is reduced in-medium one would expect that
pionic correlations will play a diminished role in an RPA calculation of the
nuclear responses. Therefore, the spin-longitudinal response, which was
primarily mediated by pion exchange, will be smaller relative to the
nonrelativistic case.
There is also another effect due to the change in effective nucleon mass.
The peak of
the quasifree distribution, 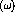 , will be
shifted relative to a naive Fermi gas model, and the distribution will
broaden,
, will be
shifted relative to a naive Fermi gas model, and the distribution will
broaden,  before any
correlations
are considered. Therefore, attractive pion correlations will act on an
uncorrelated case which is already ``hardened'' (moved to higher energy)
and the overall effect of the pion correlations much smaller than without
the relativistic corrections.
before any
correlations
are considered. Therefore, attractive pion correlations will act on an
uncorrelated case which is already ``hardened'' (moved to higher energy)
and the overall effect of the pion correlations much smaller than without
the relativistic corrections.
Michael A. Lisa
Tue Apr 1 08:52:10 EST 1997
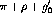 and vector
and vector 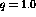 mesons, and
in the mean-field approximation these meson fields are replaced by their
classical expectation value.
In the mean-field approximation strong scalar
and vector mean-fields will cause large shifts in the in-medium mass and
energy of nucleons in the nucleons:
mesons, and
in the mean-field approximation these meson fields are replaced by their
classical expectation value.
In the mean-field approximation strong scalar
and vector mean-fields will cause large shifts in the in-medium mass and
energy of nucleons in the nucleons:

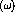 is the mean scalar field and
is the mean scalar field and  is the
free(in-medium) nucleon mass.
is the
free(in-medium) nucleon mass.
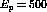 coupling constant
in the nuclear medium as [
coupling constant
in the nuclear medium as [
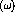 , will be
shifted relative to a naive Fermi gas model, and the distribution will
broaden,
, will be
shifted relative to a naive Fermi gas model, and the distribution will
broaden,  before any
correlations
are considered. Therefore, attractive pion correlations will act on an
uncorrelated case which is already ``hardened'' (moved to higher energy)
and the overall effect of the pion correlations much smaller than without
the relativistic corrections.
before any
correlations
are considered. Therefore, attractive pion correlations will act on an
uncorrelated case which is already ``hardened'' (moved to higher energy)
and the overall effect of the pion correlations much smaller than without
the relativistic corrections.