II. THEORETICAL UNDERPINNINGS
1. "Sub-millimeter Microwave Spectrum of H216O," Phys. Rev. A 5, 487-490 (1972). - Water as an example of SMM/THz rotational spectroscopy: Experimental and theoretical approaches
2. "Submillimeter Wave Spectra and Equilibrium Structures of the Hydrogen Halides," Phys. Rev. A 3, 1849-1857 (1971). - Rotational spectroscopy of the hydrogen halides: fundamental diatomic relations
3. "Millimeter Spectrum and Molecular Constants of Silicon Monoxide," Phys. Rev. A 15, 223-226 (1977). - Rotational spectroscopy of gas phase SiO
4. "A Study of the Rotational-Torsional Spectrum of Hydrogen Peroxide Between 80 and 700 GHz," J. Mol. Spectrosc. 85, 120-130 (1981)."The Analysis of the Rotational Spectrum of Methanol to Microwave Accuracy," J. Mol. Spectrosc. 134, 395 (1989). - Rotational spectrscopy and analysis techniques for the prototype internal rotors CH3OH and HOOH
5. "The Millimeter and Submillimeter Laboratory Spectrum of Methyl Formate (HCOOCH3) in Its Ground Symmetric Torsional State," Astrophys. J. Suppl. Ser. 55, 633-656 (1984)."The Laboratory Millimeter Wave Spectrum of Methyl Formate in its Ground Torsional E State," Astrophy. J. Suppl. 60, 949-961 (1986). - Spectroscopy and analysis of the astrophysical 'weed', methyl-formate
A number of excellent books and texts discuss the theoretical underpinnings of rotational spectra in detail. These include the early classic texts of Gordy, Smith, and Trambarulo1 and Townes and Schawlow2 as well as more recent texts by Carrington3, Kroto4, and Gordy and Cook.5 Additionally, more specialized and concise reviews have appeared.6,7 Here we will briefly discuss the underlying physics and its implications so that we can discuss the general character of THz spectroscopy and its applications. The interested reader is referred to the aforementioned texts for methods of detailed calculation.
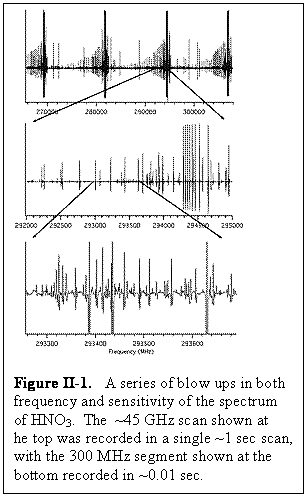
The physics that underlies spectroscopy in the THz region is very favorable. Briefly stated, THz spectroscopy is orders of magnitude more sensitive than spectroscopy in the adjacent microwave region, provides orders of magnitude greater resolution than infrared spectroscopy (especially for experimental systems of comparable size and complexity) because of smaller Doppler widths, and provides absolute quantitative analysis traceable to fundamental theory. Figure II-1 shows an example of a portion of a spectrum of a molecule of moderate size and spectral complexity, nitric acid (HNO3), which can be used to illustrate the nature of the submillimeter rotational spectra observed with the FAst Scan Submillimeter Spectroscopy Technique (FASSST) system described in Section V. Because a single FASSST scan contains ~106 frequency resolution elements, it is not possible to graphically display a complete, full band spectrum. Consequently, Fig. II-1 shows a series of blow ups in both frequency and sensitivity to provide a perspective. The ~45 GHz scan shown at the top was recorded in a single ~1 sec scan, with the 300 MHz segment shown at the bottom recorded in ~0.01 sec.

A. Absorption Strengths: If the absorption coefficient of the THz power P is defined by
![]() (II.1)
(II.1)
in the microwave limit (where hn << kT), the peak absorption coefficient between two rotational levels m and n is
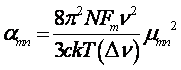 (II.2)
(II.2)
where NFm is the number of molecules per unit volume in state m, νmn is the rotational transition frequency Δν the line width, and µmn is the dipole matrix element.5 The transition moment µmn contains contributions from the components of the permanent dipole moment along each of the principal axes of the moment of inertia tensor, which determine the rotational selection rules.
For optimum sensitivity the gas pressure is adjusted in proportion to frequency so that the Doppler and pressure broadening contributions to the linewidth are equal and N/Δν is independent of frequency. Because of degeneracy and rotational partition function effects, Fm is often proportional to ν until declining Boltzmann population causes it to fall exponentially. These factors typically give rise to absorption coefficients that rise as ν3 to reach a maximum at some optimum frequency in the THz before declining exponentially. This effect can be seen in Fig. I.-1 above.
B. Energy Levels and Transitions Frequencies: The rotational energy levels of a molecule result from the quantization of its rotational kinetic energy
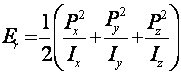 (II.3)
(II.3)
where the Pj are the components of the molecular angular momentum and the Ij are the components of the principal moments of inertia. All real molecules have additional effects (e. g. centrifugal distortion, perturbations, and internal rotations) which significantly complicate the spectroscopic problem,5 but which have minimal impact on the overall character of the spectra.
The fundamental underpinnings of the high specificity of THz spectroscopy are(1) that the rotational degree of freedom is unique in that many levels are thermally populated and (2) that the strong fundamental rotational transitions which arise from these levels are not associated with functional groups which may be constituents of many similar molecules. Rather they depend upon the global moment of inertia tensor I of the molecule. Since THz spectroscopy is sensitive to changes in each of the Ij of < 1/107, each molecule has an unique signature if even a few of the lines of its rotational structure can be detected and measured.
C. The Character of Rotational Spectra: For the most general case of an asymmetric rotor, none of the Ij are equal and the quantized rotational energy levels become
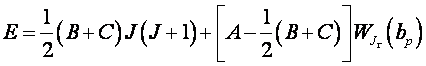 (II.4)
(II.4)
where A, B, and C are constants inversely proportional to the Ij's, and
![]() is a complicated function related to the degree of asymmetry of the molecule and angular momentum projection quantum numbers.5 However, in the prolate symmetric top limit (B = C)
is a complicated function related to the degree of asymmetry of the molecule and angular momentum projection quantum numbers.5 However, in the prolate symmetric top limit (B = C)
![]() = K2, and it is possible to use this relation along with the dipole selection rule J → J+1, ΔK = 0 to illustrate the general character of rotational spectra.
= K2, and it is possible to use this relation along with the dipole selection rule J → J+1, ΔK = 0 to illustrate the general character of rotational spectra.
Figure I.-1 above plots the absorption coefficients at 300 K for the K = 0 component of each J → J+1 transition for symmetric tops of various B values. For rigid symmetric tops, the K ≠ 0 components are degenerate with the K = 0 transitions, but for real molecules are slightly (a few MHz) displaced due to centrifugal distortion effects. In this symmetric top limit, it is straightforward to show that the values of J and ν for which rotational lines are strongest are given by
Jopt ~ 5 (T/B)1/2 (II.5)
νopt ~ 2B + 11 (BT)1/2 (II.6)
where T is the temperature in Kelvin and B a rotational constant in GHz.
For asymmetric tops the K ≠ 0 components are more widely spread according to their asymmetry and Eq. II.4, but on average have similar transition strengths. Additionally, because of the lower symmetry of asymmetric rotors, components of the dipole moment can exist along each of the three axes and a new set of selection rules and spectra will appear for each. Although this can lead to a spectrum of great complexity, the character of the symmetric tops is representative of the average spectral density, distribution in frequency, and strength of lines. Although the complete spectral assignment of asymmetric rotors can be a complex task, from many perspectives it is unnecessary because either a reference spectrum can be recorded and archived or any of several spectral catalogues can be consulted.8, 9 (8) (9)
Figure I.-1 also shows that as B decreases, there are more thermally populated transitions, and that the lines are more closely spaced and weaker. Calculations show that the average spacing of rotational lines becomes equal to the Doppler width for molecules whose rotational constants are ~ 0.1 GHz. For molecules whose atoms have masses similar to those of HNO3, the rotational constants are ~ 0.1 GHz for molecules of mass ~1000 AMU.
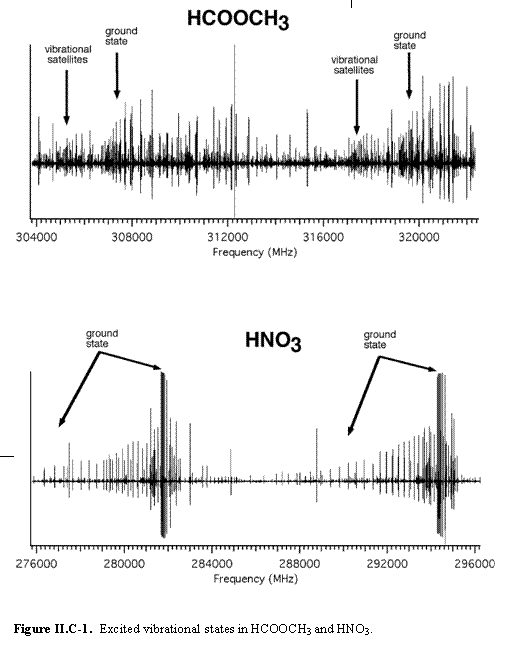
Figure II.C-1 also illustrates another important feature of rotational spectra in the THz region: the contributions from pure rotational transitions in excited vibrational states. Because methyl formate (HCOOCH3) has larger rotational constants (A, B, C) than nitric acid (HNO3), it has a sparser pure rotational spectrum. However, because it has low lying (< kT) torsional and vibrational states, many of these contribute spectra of intensity similar to that of the ground state and contribute to the much denser spectrum shown in the figure. It is likely that molecules of ~1000 AMU will have many low lying, thermally populated states, thereby leading to a more congested spectrum than in the simple estimate above. On the other hand, molecules of ~1000 AMU made of heavier atoms than HNO3 will have larger rotational constants and less dense spectra. This large molecule limit is an interesting and as yet unexplored topic in rotational spectroscopy, which will ultimately place the limit on the mass and size of molecules that have highly specific rotational signatures.
D. Rotation - Vibration Spectra: Although rotational spectra are unique to molecules, molecules also have spectra associated with their electronic, vibrational, and nuclear degrees of freedom. It is fortuitous that for most species the characteristic energies associated with each of these is separated from its neighbor by perhaps two orders of magnitude. Quantum mechanically, this allows the molecular wave function to be separated into parts and each solved separately in the context of an effective Hamiltonian. Classically, a similar picture evolves with the much higher speed of the more energetic motions providing average potentials for their less energetic neighbor. In both pictures, the rapid electronic motion provides an average electrostatic potential in which the nuclei vibrate, the average positions of the vibrating nuclei provide the moments of rotational inertia, etc.
This large separation in energy also leads to a relation between each degree of freedom and a portion of the electromagnetic spectrum: The electronic and the optical, the vibrational and the infrared, the rotational and the microwave, and the nuclear hyperfine interactions and the radio. As a result rather independent communities grew up around each of these combinations. However, while still rather distinct communities, the rotational (microwave) and vibrational (infrared) are being brought together by technological advances. In the early days, the resolution of infrared spectrometers was too low to resolve the rotational structure of any except the lightest (e. g. H2O) species and microwave techniques did not have the frequency coverage to measure significant rotational spectra except in much heavier molecules. However, now FTIR and diode laser techniques can resolve the Doppler limit (~100 MHz) and THz technologies have very wide spectral coverage.
As a result, it is now common for "infrared" analyses to contain measured microwave data in large weighted least-squares analyses. Nitric acid provides a useful specific example. For this species infrared techniques have been used to study the rotational structure of all of its fundamental vibrations. THz techniques have now been used to study not only the molecules which reside in the ground vibrational state, but also the rotational structure of molecules in many of the excited vibrational states. While the thermal population in the excited states is reduced by the Boltzmann factor (e. g. the ν5 vibrational state lies at ~900 cm-1 and has a thermal population of ~1%), the resolution and sensitivity of THz spectroscopy makes the study of these small populations reasonably straightforward. For example, Fig. II.D-1 shows THz spectra of a number of these transitions which were recorded with a FASSST spectrometer with ~10-6 sec of integration time. For molecules such as HNO3 for which it is possible to record THz spectra over a large portion of its thermally populated rotational spectra, weighted infrared - THz fits are completely dominated by the higher accuracy THz data (the weighting ratio is typically 106). In fact, it has been shown that an analysis of the THz data can predict (except for the central vibrational frequency itself!), the entire infrared spectra to unprecedented accuracy. While this is useful for species such as HNO3 (especially in highly congested and perturbed regions of its spectrum), its real promise lies in somewhat heavier species (e. g. ClONO2) whose spectra are unresolved or marginally resolved in the Doppler limit in the infrared. The detailed ro-vibration structure of these species is of considerable interest for the recovery of atmospheric remote sensing information. This requires accurate modeling of the pressure and temperature variation of the recovered profiles. These can only be obtained by a detailed line model, which can be synthesized from analyses of the THz rotational structure in both the ground and upper vibrational state of the infrared band of interest.
Figure II.D-1. Spectrum of HNO3 which shows the absorptions in the excited ν5 vibrations states marked with crosses.
|
References
[1] W. Gordy, W. V. Smith, and R. F. Trambarulo, Microwave Spectroscopy. New York: John Wiley and Sons, 1953.
[2] C. H. Townes and A. L. Schawlow, Microwave Spectroscopy. New York: McGraw-Hill Dover Publications, Inc., 1955.
[3] A. Carrington, Microwave Spectroscopy of Free Radicals. London: Academic Press, 1974.
[4] H. W. Kroto, Molecular Rotation Spectra. London: Wiley, 1975.
[5] W. Gordy and R. L. Cook, Microwave Molecular Spectra, vol. 18, Third ed. New York: John Wiley & Sons, 1984.
[6] R. L. Cook, "Microwave Spectroscopy," in Macmillan Encyclopedia of Chemistry: Macmillan Press, 1997.
[7] R. L. Cook, "Molecular Microwave Spectroscopy," in Encyclopedia of Physical Science and Tecnology, R. A. Meyers, Ed., 3rd ed: Academic Press, 2000.
[8] H. M. Pickett, R. L. Poynter, E. A. Cohen, M. L. Delitsky, J. C. Pearson, and H. S. P. Muller, "Submillimeter, Millimeter, and Microwave Spectral Line Catalog," J. Quant. Spectrosc. Rad. Transfer, vol. 60, pp. 883-890, 1998.
[9] L. S. Rothman, C. P. Rinsland, A. Goldman, S. T. Massie, D. P. Edwards, J.-M. Flaud, A. Perrin, C. Camy-Peyret, V. Dana, J.-Y. Mandin, J. Schroeder, A. Mccann, R. R. Gamache, R. B. Wattson, K. Yoshino, K. V. Chance, K. W. Jucks, L. R. Brown, V. Nemtchinov, and P. Varanasi, "The HITRAN Molecular Spectroscopic Database and HAWKS (HITRAN Atmospheric Workstation): 1996 Edition," J. Quant. Spectrosc. Radiat. Transfer, vol. 60, pp. 665-710, 1998.