Trivedi Group
Site Navigation
Ultracold Atoms in Optical Lattices
The observation of Bose-Einstein Condensation in trapped ultra-cold atoms was a technological breakthrough. With the addition of an optical lattice, these systems become nearly perfect experimental realizations of the Bose-Hubbard Model (BHM). Understanding their behavior is the next step toward applications and emulation of other condensed matter systems thought to be described by the BHM such as high-temperature superconductors. Unfortunately, definitive identification of the Superfluid and Mott Insulator phases, the temperature and other properties remains elusive. We are using numerical methods to characterize phases and conditions at finite temperatures in optical traps filled with bosons.
Directed-Loop Algorithm -- A type of quantum Monte-Carlo that allows experimental-scale (106 bosons) simulation of the Bose-Hubbard Model. This is a continuous- and imaginary-time path integral expansion of the hamiltonian..
Local Density Approximation -- Applies DLA to a physical trap. Assumes the chemical potential decreases harmonically with distance from the center of the trap.
Wannier States -- Maps experimental parameters, such as laser intensity and frequency, onto the hopping and on-site interaction values of the Bose-Hubbard Model.
Sharp peaks in the momentum distribution of bosons in optical lattices in the normal state:
Yasuyuki Kato, Qi Zhou, Naoki Kawashima and Nandini Trivedi, Nature Physics 4, 617 - 621 (2008)
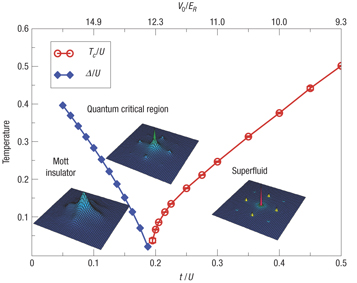
The superfluid transition temperature Tc (red) and the single-particle energy gap Delta in the Mott insulator (blue) vanish at the quantum phase transition as a function of tuning t/U, the ratio of hopping to onsite repulsion. The typical interference patterns in the superfluid, Mott and critical regions are also shown.
Direct mapping of the finite Temperature Phase Diagram
of Strongly Correlated Quantum Models:
Qi Zhou, Yasuyuki Kato, Naoki Kawashima, Nandini Trivedi, Phys. Rev. Lett. 103, 085701 (2009)
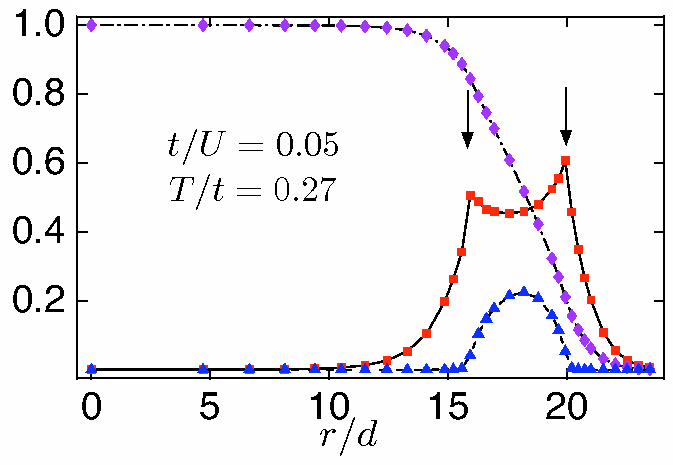
Origin of kinks: The local density ρh(μ(r))
(purple diamonds), compressibility κh(μ(r)) (red
boxes) and superfluid density ρhs(μ(r)) (blue triangles) as functions
of the radial coordinate in the trap. A finite ρs develops
in some portion of the trap, κ(r) shows sharp kinks. The location
of these kinks coincides with the Superfluid-Normal state boundary in the trap.
Thermometry and Nonequilibrium effects: (E. Duchon)
Dynamics across quantum phase transitions: (M. Swanson)
Fermions in optical Lattices:
Title, reference, authors
One of the major challenges in realizing antiferromagnetic and superfluid phases in optical lattices is the ability to cool fermions. We determine constraints on the entropy for observing these phases in two-dimensional Hubbard models using determinantal quantum Monte Carlo simulations.
"Fermions in 2D Optical Lattices: Temperature and Entropy Scales for Observing Antiferromagnetism and Superfluidity", Thereza Paiva, Richard Scalettar, Mohit Randeria, and Nandini Trivedi, Phys. Rev. Lett. 104, 066406 (2010)
Ferromagnetism in the Fermi Gas of ultracold atoms:
It is amazing that we do not know the ground state of a system of fermions interacting with repulsive interactons. A dilute and ultracold gas of alkali atoms is the perfect test bed for investigating this question as was done in a recent experiment by MIT group (G. B. Jo et al, Science 325, 1521-1524 (2009)). They claimed to have found a transition to a ferromagnetic state in the strongly interacting regime of the fermions. There are several questions about the lack of observation of ferromagnetic domains and non-equilibrium effects that shed some doubt on the experiments.
Our aim is to perform accurate quantum Monte Carlo calculations coupled with simple analytical methods based on the cluster expansion of the density to investigate the stability of the ferromagnetic phase. (S. Y. Chang, M. Randeria)
Larkin-Ovchinnikov phases of imbalanced Fermi gases in optical lattices:
A Fermi gas with attractive interactions between two hyperfine species exhibits BCS/BEC pairing, like dancers in a ballroom. What happens if there is a population imbalance between the two species? Do the extra dancers phase-separate to form a "singles club", dissolve into the crowd, or force the couples to break up?
We find that instead of the extra dances separating, a fascinating new type of superfluid known as a Larkin-Ovchinnikov (LO) phase gets formed. In this LO phase the superfluid order parameter changes sign from positive to negative and in the regions where the superfluid order is zero, called a domain wall, the excess polarization gets confined.
Unlike continuum Fermi gases, where LO behavior occurs in a tiny sliver of the phase diagram, optical lattices have LO states for a large range of parameters. Moreover, these LO states have signatures in real space, momentum space, and energy spectra that may be experimentally detectable; in particular, the domain-wall polarization may be observable using phase-contrast methods with the present experimental resolution. (Y. L. Loh)
Submitted to Phys. Rev. Lett. , preprint: "Large Range of Stability of Larkin-Ovchinnikov States for Imbalanced Fermi Gases in Optical Lattices", Y. L. Loh and N. Trivedi, arXiv:0907.0679v1
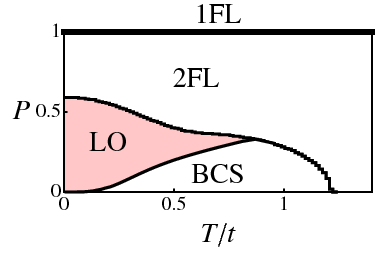
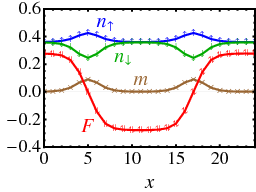
Left: Phase diagram of the cubic lattice attractive Hubbard model, as a function of polarization fraction P and temperature T, at U=-6t (weak-to-medium coupling) and μ=0 (half-filling). 2FL and 1FL represent two- and one-species Fermi liquids. Right: Pairing density F, magnetization m, and number densities n as a function of position x, for a "strong Larkin-Ovchinnikov state" on a 24x20x29 cubic lattice (T=0.01t, U=-4t, μ=-0.5t, h=0.85t).