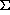 ADC), and its two neighbors are used.
Neglecting for the moment finite-
ADC), and its two neighbors are used.
Neglecting for the moment finite- and finite electron number
effects, the uncertainty of measuring the centroid of the Gaussian shows
a linear dependence on the uncertainty of the ADC projections [8]:
and finite electron number
effects, the uncertainty of measuring the centroid of the Gaussian shows
a linear dependence on the uncertainty of the ADC projections [8]:
The hit position in the padrow direction is fitted with a 3-point Gaussian
parametrization [3]. This fit is performed on the projection of
the ADC values onto the padrow; the pad with the largest projection
(highest 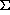 ADC), and its two neighbors are used.
Neglecting for the moment finite-
ADC), and its two neighbors are used.
Neglecting for the moment finite- and finite electron number
effects, the uncertainty of measuring the centroid of the Gaussian shows
a linear dependence on the uncertainty of the ADC projections [8]:
and finite electron number
effects, the uncertainty of measuring the centroid of the Gaussian shows
a linear dependence on the uncertainty of the ADC projections [8]:
where 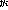 and
and 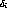 are the pad projections and their uncertainties,
respectively,
are the pad projections and their uncertainties,
respectively, 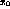 is the centroid position relative to a pad edge, and
is the centroid position relative to a pad edge, and
 is the pad pitch.
is the pad pitch.
What is the uncertainty on the pad projection (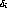 ) to use in
Equation 6? The noise for the signal on each pixel
comes from 3 sources [1]: (1) electronic noise originating before
or in the shaper amplifier (SAS),
(2) electronic noise in the switched capacitor array (SCA) chip, and
(3) digitization noise-- here meaning the ``noise'' associated with rounding
a number to integer value.
The noise contribution from the second and third terms varies randomly from
bucket to bucket, and so is ``white'' noise. However, the noise signal
coming through the SAS is filtered with the repsonse function of the amplifier,
and so the noise signal on one bucket is correlated with that on the following
bucket; see Figure 12.
) to use in
Equation 6? The noise for the signal on each pixel
comes from 3 sources [1]: (1) electronic noise originating before
or in the shaper amplifier (SAS),
(2) electronic noise in the switched capacitor array (SCA) chip, and
(3) digitization noise-- here meaning the ``noise'' associated with rounding
a number to integer value.
The noise contribution from the second and third terms varies randomly from
bucket to bucket, and so is ``white'' noise. However, the noise signal
coming through the SAS is filtered with the repsonse function of the amplifier,
and so the noise signal on one bucket is correlated with that on the following
bucket; see Figure 12.

Figure 12: A random (``white')' noise spectrum is compared to a filtered
noise spectrum, offset on the y-axis.
Time sampling corresponds to using 1024 time buckets on each side of
the TPC. Both spectra are normalized to have
unit RMS. Noise coming through the SAS will be correlated in time, due
to finite bandwidth; therefore, the error on the sum of consecutive time
buckets will not add in quadrature.
If the SAS noise were white (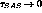 ) then the
error on a pad projection would be
) then the
error on a pad projection would be
where 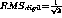 in ADC counts, and
in ADC counts, and 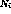 is the
number of pixels that contribute to the pad projection.
is the
number of pixels that contribute to the pad projection.
If the SAS had an extremely long time constant
(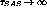 ),
then all pixels contributing to a pad projection would be shifted by the
same amount by the SAS, so that
),
then all pixels contributing to a pad projection would be shifted by the
same amount by the SAS, so that
Equations 7 and 8 represent extreme cases,
as 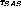 is in reality on the order of the sampling time. Since
the SAS contributes heavily to
the noise (800
is in reality on the order of the sampling time. Since
the SAS contributes heavily to
the noise (800 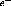 RMS, corresponding to 1.19 ADC counts, as compared
to 0.45 and 0.71 ADC counts RMS from SCA and digitization, respectively),
it does matter which equation one chooses. Simulations with 512 time
samples in P-10 suggest that N
RMS, corresponding to 1.19 ADC counts, as compared
to 0.45 and 0.71 ADC counts RMS from SCA and digitization, respectively),
it does matter which equation one chooses. Simulations with 512 time
samples in P-10 suggest that N 9, so that the
9, so that the 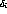 differs
by a factor of 2.5 between the two approximations. Comparison of
uncertainties to residual distributions suggests that
Equation 8 is the better approximation for
our situation, and that is what
is used in TPH. See also Section 6.3.
differs
by a factor of 2.5 between the two approximations. Comparison of
uncertainties to residual distributions suggests that
Equation 8 is the better approximation for
our situation, and that is what
is used in TPH. See also Section 6.3.
Calculation of the centroid uncertainty for a 3-point Gaussian fit is
straightforward.
However, the facts that (1) the signal originated through the creation of
a finite number of primary electrons (or electron clusters), and
(2) from a track that crosses the padrow at a non-zero angle  ,
also affect the spatial resolution in the TPC,
quickly dominating it, in fact.
The position resolution then takes a form [9]
,
also affect the spatial resolution in the TPC,
quickly dominating it, in fact.
The position resolution then takes a form [9]
where 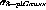 represents the centroid uncertainty from
Equation 6, and L is the drift distance for the hit.
The second and third terms represent the
contributions to the uncertainty from finite electron number and finite
crossing angle effects, respectively. In Equation 9,
represents the centroid uncertainty from
Equation 6, and L is the drift distance for the hit.
The second and third terms represent the
contributions to the uncertainty from finite electron number and finite
crossing angle effects, respectively. In Equation 9,
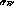 and
and 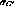 are constants, depending only
on detector geometry and TPC gas [9].
These constants must be determined empirically. See Section
6.3.
are constants, depending only
on detector geometry and TPC gas [9].
These constants must be determined empirically. See Section
6.3.
Note the competing dependencies in
the three terms in Equation 9. For example, the
first and second terms decrease with increased signal size, while
the third increases. This is important, as this third term
quickly dominates the resolution. See Figure 13
for calculations
of the spatial resolution in the outer sector using P-10 gas in the
TPC. It is seen that the so-called ``intrinsic resolution,'' which
depends on the signal:noise and is given
by Equation 6, rapidly becomes insignificant compared
to finite- effects, especially for larger signals. We note
that this behaviour, in particular, may change if delta electron production
changes in STAR Geant simulations.
effects, especially for larger signals. We note
that this behaviour, in particular, may change if delta electron production
changes in STAR Geant simulations.
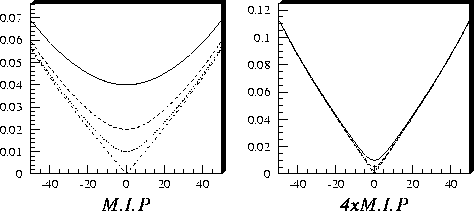
Figure 13: Position resolution as a function of crossing angle
 in the outer sector using P-10 gas, according to our
parametrization. Resolution for
minimum ionizing particle hits (m.i.p) and hits 4 times as large are
shown. Curves are shown for zero noise (dotdash lines), the default
settings of the slow simulator (dotted curves), twice the default noise
in the simulator (dashed curves), and 4x the noise in the simulator (solid
curves). This last case corresponds roughly to the situation considered in
the STAR CDR, where, in addition, a slightly different pad geometry was
assumed.
in the outer sector using P-10 gas, according to our
parametrization. Resolution for
minimum ionizing particle hits (m.i.p) and hits 4 times as large are
shown. Curves are shown for zero noise (dotdash lines), the default
settings of the slow simulator (dotted curves), twice the default noise
in the simulator (dashed curves), and 4x the noise in the simulator (solid
curves). This last case corresponds roughly to the situation considered in
the STAR CDR, where, in addition, a slightly different pad geometry was
assumed.
For this reason, the position uncertainty cannot be determined at the
hitfinding level. Any attempt at this level to produce an ``average error''
whose distribution resembles that of the average residual distribution
would be an unsatisfactory comprise that overestimates the uncertainty
of some hits while underestimating that of others. TPH enters
the value given by Equation 6 in TPHIT.DX and TPHIT.DY. From
this information, knowlege of the constants 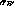 and
and
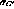 , the energy loss of the track (in TPHIT.Q), the
drift distance (from TPHIT.Z), and a
hypothesis of the crossing angle
, the energy loss of the track (in TPHIT.Q), the
drift distance (from TPHIT.Z), and a
hypothesis of the crossing angle  , the position uncertainty can
be calculated hit-by-hit. Tracking software must then update these
uncertainties DX and DY, as information becomes available about the
parent track.
, the position uncertainty can
be calculated hit-by-hit. Tracking software must then update these
uncertainties DX and DY, as information becomes available about the
parent track.