
Mail:
Dept. of Chemistry
Ohio State University
100 W. 18th Ave.
Columbus, OH 43210
Office:
412 CBEC
Email:
herbert@
chemistry.ohio-state.edu
|
|
Indinavir (an anti-retrovial, in red) in the binding pocket of HIV-2 protease |
Fragment-based quantum chemistry methods attempt to decompose an impossibly large ab initio calculation into tractable subsystems, using physics-based approximations to distribute the computing effort across a large number of small calculations. The idea is to take a method whose cost scales as O(Np), where the exponent p reflects the intrinsic cost of the quantum-mechanical model [e.g., p = 7 for CCSD(T)], and reduce this cost to Nfrag × O(np), where n represents the subsystem size. One can imagine that n represents the intrinsic length scale of quantum mechanics; then fragmentation methods amount to a way to introduce classical approximations on-the-fly at longer length scales.
A wide variety of fragment-based approximations exist in the literature, with widely varying accuracy. We have shown how they can be unified under a common theoretical framework that we call the generalized many-body expansion (GMBE). In addition to clarifying connections between existing methods, this formalism suugests new approximations that appear to offer a promising route toward high-accuracy, fragment-based calculations in large polyatomic molecules, including proteins. An overview of the whole field of fragment-based quantum chemistry can be found in a recent "Perspective" article.
|
|
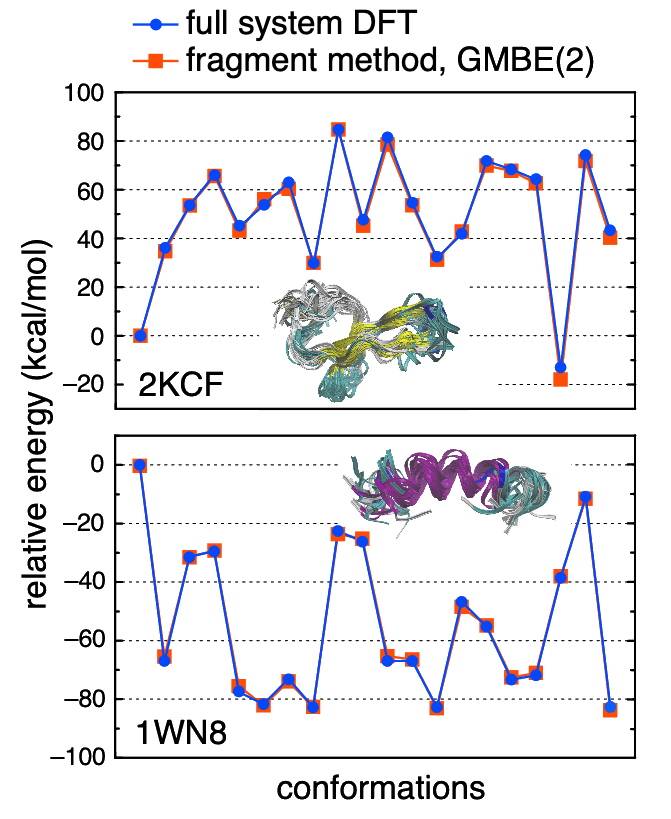
M06-2X/6-31G* energies for ensembles of protein conformations. The fragment method requires calculations no larger than four amino acids. |
The GMBE formalism tessellates a system into overlapping fragments, using intersections of those fragments to avoid double counting. By including dimers of overlapping fragments [GMBE(2) approach], one includes both through-bond and through-space interactions. Using fragments as small as two amino acides (hence subsystems up to four amino acids), GMBE(2) calculations faithfully reproduce full-system DFT calculations for proteins. The fragments are small enough that it should be possible to push this to even higher levels of theory, to obtain ab initio-quality energetics in macromolecular systems.
To achieve good accuracy, fragmentation methods often use some form of electrostatic embedding, where point charges or other electrostatic parameters are derived from the fragment wavefunctions and used to incorporate many-body polarization effects. One can think of this as a form of on-the-fly, homogeneous QM/MM calculation where the MM part is iteratively updated as each fragment's wavefunction is computed in the electrostatic environment of the other fragments, with the whole scheme iterated to mutual self-consistency (similar to the XPol approach that we use in XSAPT calculations.) If not done carefully, however, electrostatic embedding can significantly complicate the formulation of analytic energy gradients ∂E/∂x, because perturbing the nuclei on one fragment modifies the point charges on that fragment, which then has a nonlocal effect on the other fragments. Mathematically, this manifests as charge-response terms in the analytic gradient, which are technically complicated (they are not part of standard QM/MM machinery) and are thus often ignored, to the detriment of energy conservation in ab initio molecular dynamics simulations.
|
|
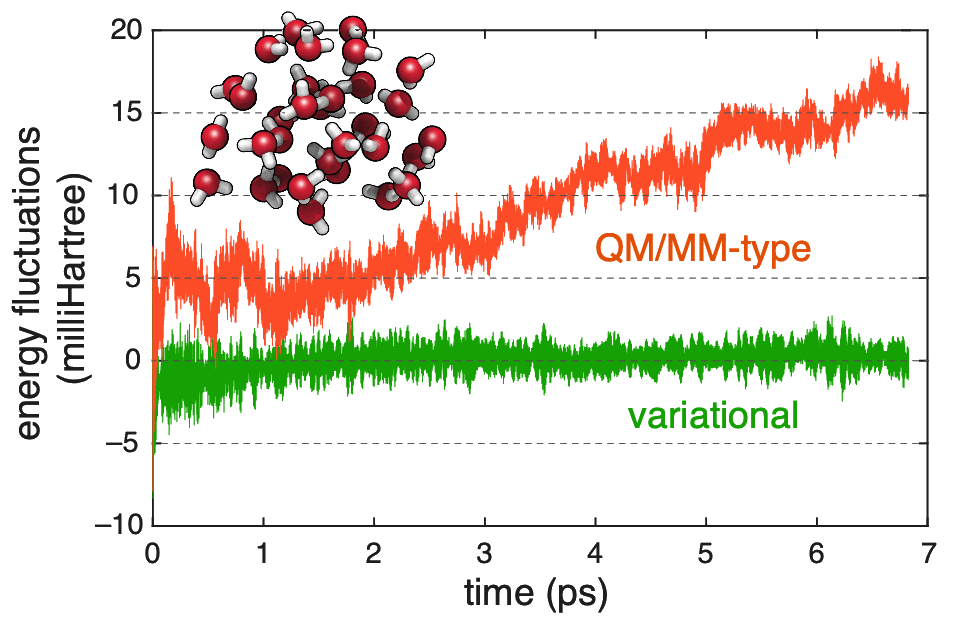
Energy conservation in fragment-based ab initio MD, comparing a variational formalism with proper gradients to a QM/MM-type formalism that lack charge-response terms. |
We have developed a variational formulation of the GMBE that facilitates rigorously correct analytic gradients, without the need to solve coupled-perturbed equations for the fragments, although it still requires modification of the fragment Fock matrices with respect to a standard QM/MM formulation Ab initio molecular dynamics simulations performed with this new methodology are rigorously energy conserving, whereas attempts to implement fragment-based dynamics using off-the-shelf quantum chemistry result in serious energy drift over just a few picoseconds of simulation time!
Finally, we have shown how energy-based screening, using a low-level method (or even a classical force field) is much more efficacious at reducing the requisite number of electronic structure calculations, as compared to conventional cost-reduction strategies such as distance-based thresholds. Use of energy-based screening affords a fragmentation method whose cost is truly linear-scaling with respect to system size, is stable in large basis sets (including those containing diffuse functions), and is capable of achieving accuracy of 1 kcal/mol accuracy even for challenging problems such as the relative energies of water cluster isomers.