programs to enumerate hydrogen bond topologies in ice, and generate graph invariants
Programs available on this page are the work of Chris Knight and Sherwin Singer. Corey Beck helped finish the programming, and found many bugs in the programs and in the manual.what these programs do
In the study of order/disorder phenomena in ice, an enumeration of
all possible symmetry-distinct hydrogen bond (H-bond) configurations
is required. For example, exactly 16, symmetry-distinct H-bond
configurations are possible ins a 12-water orthorhombic unit cell of
ice Ih. It is pointless to perform expensive ab initio
calculations on more structures, since that will only regenerate a
previously found energy. Furthermore, we have shown that the energy,
and other scalar physical properties, can be concisely linked to the
H-bond configuration with the use of polynomials which are invariant
to all symmetry group operations. We have called such polynomials
first, second, third,... order graph invariants when they are linear,
quadratic, cubic,... in the bond variables.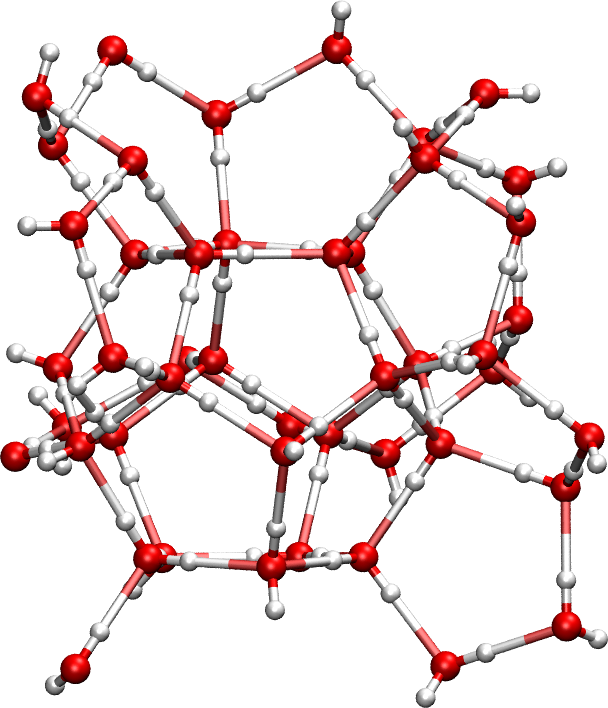
The Pm3n unit cell of a type I ice clathrate, pictured on the right, contains 46 water molecules. These FORTRAN programs will tell you that exactly 17,151,190 symmetry distinct H-bond structures are possible. (Click here for the input files in a tar.gz archive, prepared by Corey Beck.) Sometimes Monte Carlo sampling of H-bond configurations is preferred. In other situations, it is very useful to have all possible hydrogen bond topologies in hand. You can also generate all first and second order graph invariants for this system.
Besides the manual that is part of the program package, and the two primary articles listed below, the applications presented in other journal articles may illustrate and clarify the techniques.
Currently, programs for periodic unit cells for ice are available. Eventually, we will make programs for finite water clusters available as well.
Production of these programs were made possible by support from the National Science Foundation.
downloads
- programs, sample input files, and manual in a tar.gz archive
- input files to generate all symmetry-distinct H-bond configurations of a type I ice clathrate (Prepared by Corey Beck.)
some relevant publications
- Jer-Lai Kuo, James V. Coe, Sherwin J. Singer, Yehuda B. Band, and Lars Ojamäe, ``On the use of graph invariants for efficiently generating hydrogen bond topologies and predicting physical properties of water clusters and ice'', J. Chem. Phys. 114(6):2527 (2001).
- Jer-Lai Kuo and Sherwin J. Singer, ``Graph invariants for periodic systems: towards predicting physical properties from the hydrogen bond topology of ice'', Phys. Rev.E67(1):016114 (2003).
- Sherwin J. Singer, Jer-Lai Kuo, Tomas K. Hirsch, Chris Knight, Lars Ojamäe and Michael L. Klein, ``Hydrogen bond topology and the ice VII/VIII and Ih/XI proton ordering phase transitions'', Phys.Rev.Lett. 94(13):135701 (2005).
- Chris Knight and Sherwin J. Singer, ``Prediction of a phase transition to a hydrogen bond ordered form of ice VI'', J.Phys.Chem. B109(44):21040 (2005).
- Chris Knight, Sherwin J. Singer, Jer-Lai Kuo, Tomas K. Hirsch, Lars Ojamäe and Michael L. Klein, ``Hydrogen bond topology and the ice VII/VIII and Ih/XI proton ordering phase transitions'', Phys.Rev. E73(5):056113 (2006).
- Chris Knight and Sherwin J. Singer, ``Tackling the problem of hydrogen bond order and disorder'', Physics and Chemistry of Ice (Proceedings of the 11th International Conference on the Physics and Chemistry of Ice), ed., Werner F. Kuhs (Royal Soc. of Chemistry, 2007), p.329.
- Chris Knight and Sherwin J. Singer, ``Theoretical study of a hydroxide ion within the ice-Ih lattice'', Physics and Chemistry of Ice (Proceedings of the 11th International Conference on the Physics and Chemistry of Ice), ed., Werner F. Kuhs (Royal Soc. of Chemistry, 2007), p.339.
- Chris Knight and Sherwin J. Singer, ``Hydrogen bond ordering in ice V and the transition to ice XIII'', J. Chem. Phys. 129(16):164513 (2008).
- Chris Knight and Sherwin J. Singer, ``Site disorder in ice VII arising from hydrogen bond fluctuations'', J. Phys. Chem. A113(45):12433 (2009).