• Research
• People
• JMH Bio / CV
• Publications
• Funding
• Group meeting

Mail:
Dept. of Chemistry
Ohio State University
100 W. 18th Ave.
Columbus, OH 43210

Office:
412 CBEC

Email:
herbert@
chemistry.ohio-state.edu

John Herbert research group

Improved algorithms for ab initio molecular dynamics

Spin density of the aqueous electron, e–(aq), from an AIMD simulation

Overview

Efficient algorithms developed in our group are expanding the frontiers of ab initio molecular dynamics (AIMD) simulations, in which on-the-fly quantum chemistry is used to calculate the forces required for a classical molecular dynamics simulation, thus obviating the need for parametrized force fields. This is especially important for unusual or reactive species (such as the hydrated electron and other aqueous radicals), for which it is extremely difficult to construct accurate force fields. Improvements to the efficiency of AIMD algorithms translate directly into longer simulation time scales and larger system sizes, for a fixed quantity of computer resources. Our Fock matrix extrapolation algorithm is amongst the preferred ways to accelerate AIMD. We have also developed the QM/MM-Ewald method for incorporating periodic boundary conditions into QM/MM calculations, in a manner that is robust in arbitrary basis sets.

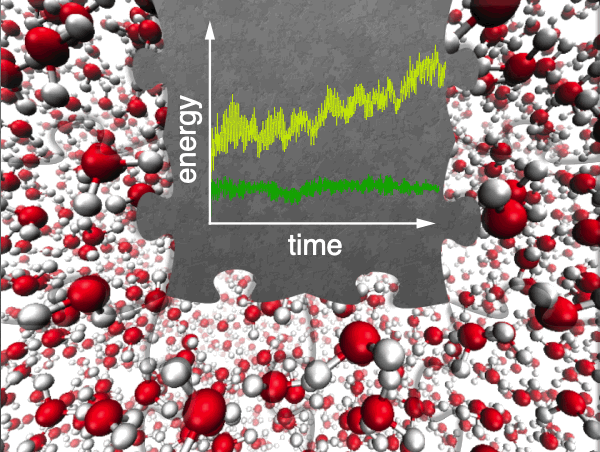
Monitoring energy conservation in a fragment-based AIMD simulation. Only with rigorously correct gradients is energy conserved.

Especially for a system such as liquid water, which would seem to divide up into small fragments in a natural way, there is significant interest in using fragment-based quantum chemistry approaches to accelerate AIMD calculations, and numerous algorithms have been proposed. Many of these represent a form of QM/MM simulation in which fragment-based wave function calculations are used to obtain classical MM force-field parameters "on the fly". This form of classical embedding, however, can significantly complicate the analytic gradient formalism for the underlying QM method, and many incorrect analytic gradients have been reported in the literature. Energy conservation in classical MD simulations is known to be exquisitely sensitive to the accuracy and consistency of the forces, so many of these fragment-based approaches are fundamentally ill-posed for dynamics applications. We have recently reported a variational formalism for fragment-based QM/MM embedding, which greatly simplifies the formulation of analytic gradients, without introducing approximations, providing for energy-conserving simulations based on fragmentation.

Representative Publications

• Variational formulation of the generalized many-body expansion with self-consistent charge embedding: Simple and correct analytic energy gradient for fragment-based ab initio molecular dynamics. J. Liu, B. Rana, K.-Y. Liu, and J. M. Herbert, J. Phys. Chem. Lett. 10, 3877–3886 (2019).


• Analytic gradient for the QM/MM-Ewald method using charges derived from the electrostatic potential: Theory, implementation, and application to ab initio molecular dynamics simulation of the aqueous electron. Z. C. Holden, B. Rana, and J. M. Herbert, J. Chem. Phys. 150, 144115:1–20 (2019).


• Accelerated, energy-conserving Born-Oppenheimer molecular dynamics via Fock matrix extrapolation. J. M. Herbert and M. Head-Gordon, Phys. Chem. Chem. Phys. 7, 3269–3275 (2005).


• Curvy-steps approach to constraint-free extended-Lagrangian ab initio molecular dynamics using atom-centered basis functions: Convergence toward Born-Oppenheimer trajectories. J. M. Herbert and M. Head-Gordon, J. Chem. Phys. 121, 11542:1–15 (2004).