
Mail:
Dept. of Chemistry
Ohio State University
100 W. 18th Ave.
Columbus, OH 43210
Office:
412 CBEC
Email:
herbert@
chemistry.ohio-state.edu
|
|
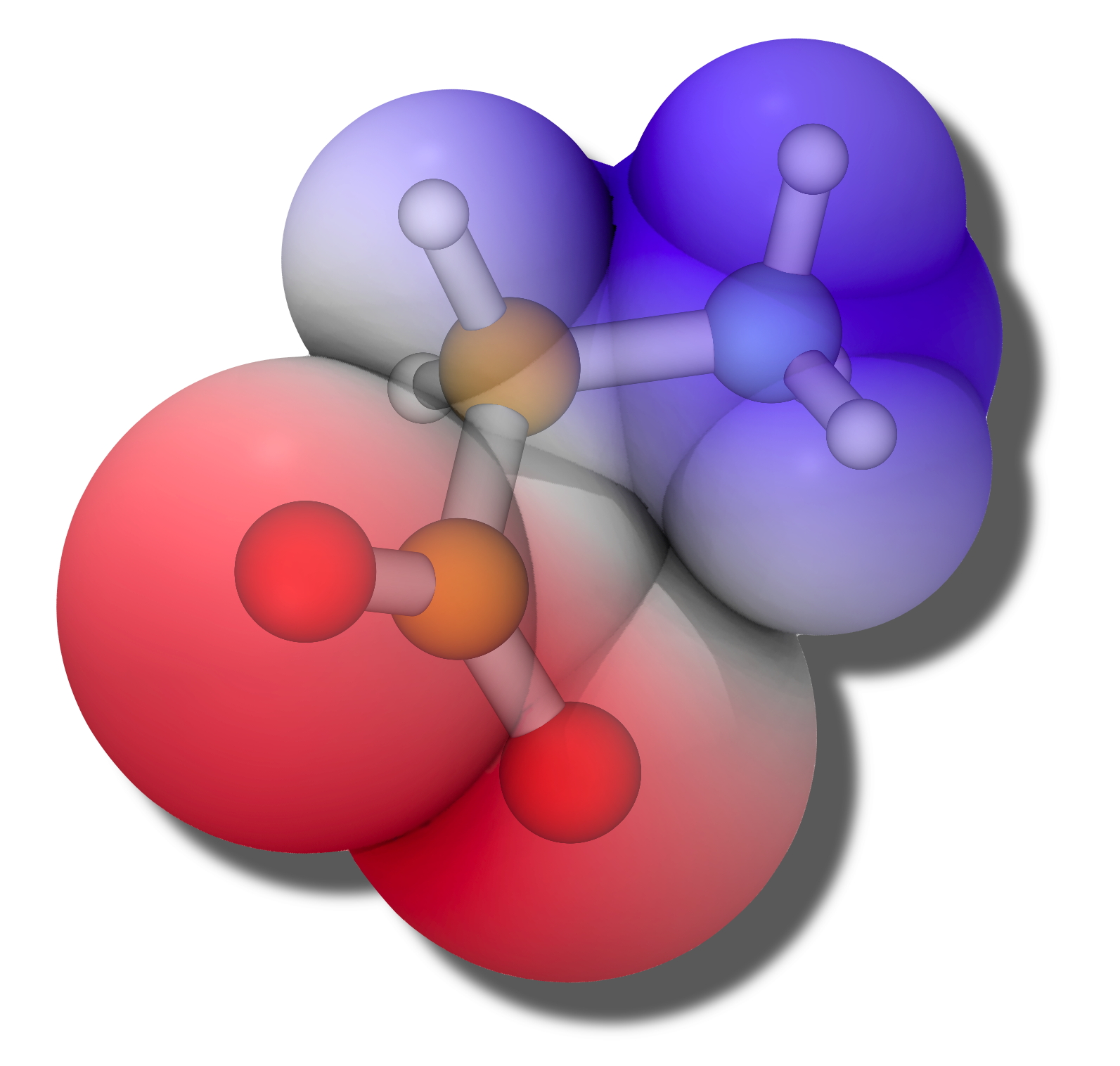
Electrostatic potential map at the solute/continuum interface |
Apparent surface charge, reaction-field solvation models, better known as "polarizable continuum models" (PCMs), represent the most widely-used class of implicit solvent models in quantum chemistry. Given a definition for a solute cavity (e.g., a van der Waals surface) that defines the interface between the solute molecule and the structureless dielectric representation of the solvent, these models provide an approximate solution for Poisson's equation or the linearized Poisson-Boltzmann equation using relatively efficient two-dimensional surface integration, rather than the three-dimensional sampling that is required to solve these differential equations directly. PCMs greatly accelerate conformational or phase-space sampling, since explicit solvent degrees of freedom are absent. Furthermore, as compared to empirical solvation models that are intended only to predict solvation free energies, PCMs are physically-motivated models that are directly interwoven into the system's Hamiltonian, and can thus be used to explore the effects of solvation on a variety of chemical and physical properties. These include solution-phase geometries, vibrational frequencies, electronic excitation energies, and more.
Elimination of explicit solvent molecules also greatly simplifies geometry optimizations and molecular dynamics simulations. This is especially true for excited electronic states. Compared to the ground state, where one can often view geometry optimization and molecular dynamics algorithms as "black boxes", moving about on excited-state potential surfaces is often considerably more complicated, owing to state crossing and near-degeneracies between excited states. We are currently endeavoring to exploit PCMs to explore excited-state potential energy surfaces for macromolecular systems. In addition, the development of higher-accuracy solvation models continues, especially with regard to the non-electrostatic contributions to the solvation energy, such as the dispersion and cavitation energies, and we are beginning to explore these models as alternatives to grid-based three-dimensional Poisson-Boltzmann solvers in biomolecular implicit solvent simulations. The PCMs that we are developing are much more physics-based than other (more empirical) implicit solvent models, and offer an attractive way to enhance conformational sampling in classical MD simulations. We have recently developed a version for anisotropic solvation environments such as the air/water interface.
|
|
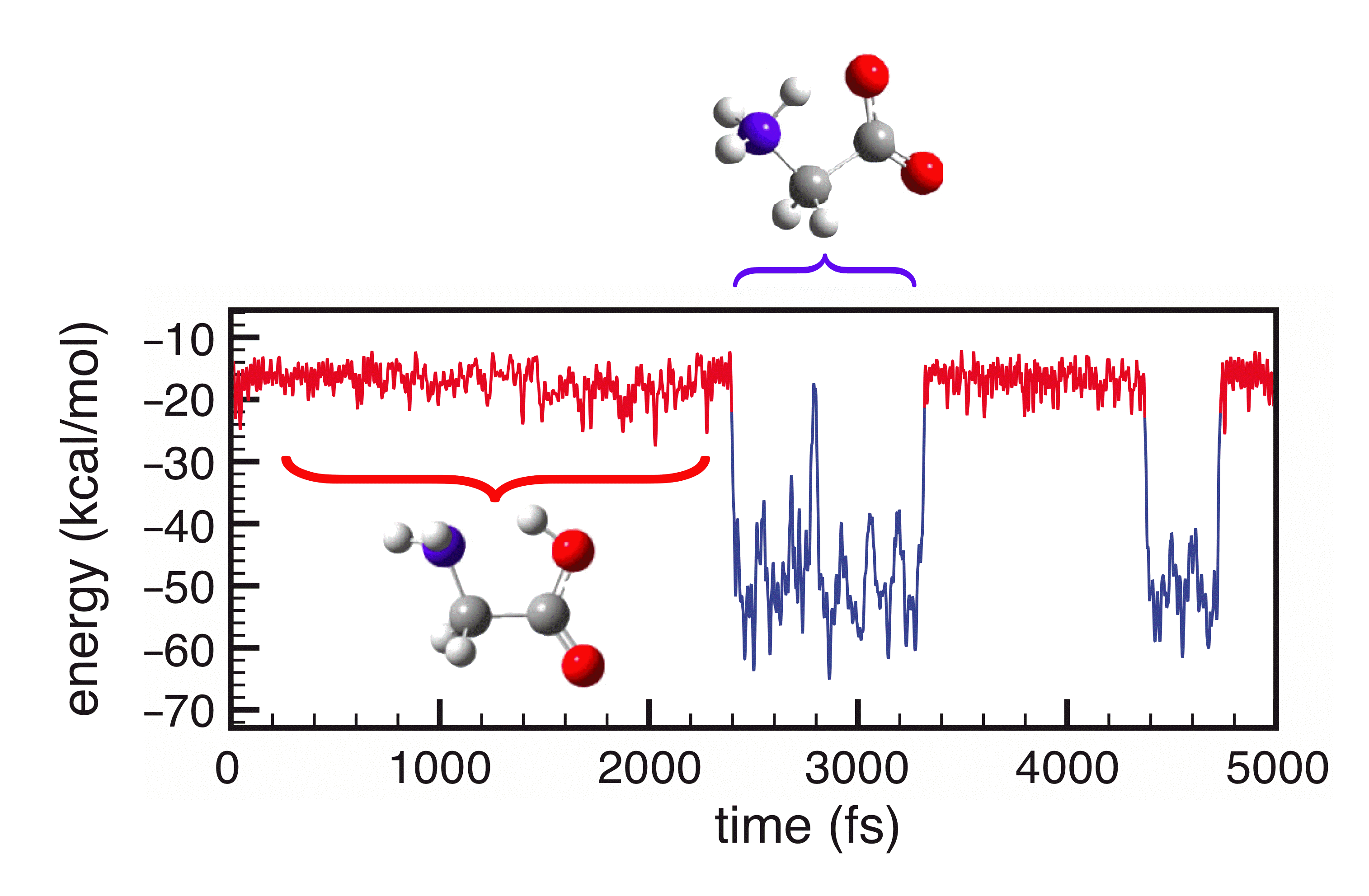
Molecular dynamics simulation of forward and reverse proton transfer between two tautomers of glycine. The solvent is a continuum model of water. |
We have recently revisited the numerical implementation of several widely-used PCMs, and have developed a new technique (the "switching/Gaussian" approach) for discretizing the integral equations that define these models. Our approach guarantees that the solute's potential energy surface is a smooth function of the nuclear coordinates, and also eliminates certain numerical artifacts inherent to some PCM implementations. As such, these PCMs can be used to perform stable ab initio molecular dynamics simulations of chemical reactions, in which chemical bonds are made or broken. In such cases, the cavity shape may change abruptly and dramatically, and a smooth potential surface is essential if one is to obtain stable, energy-conserving molecular dynamics.
|
|
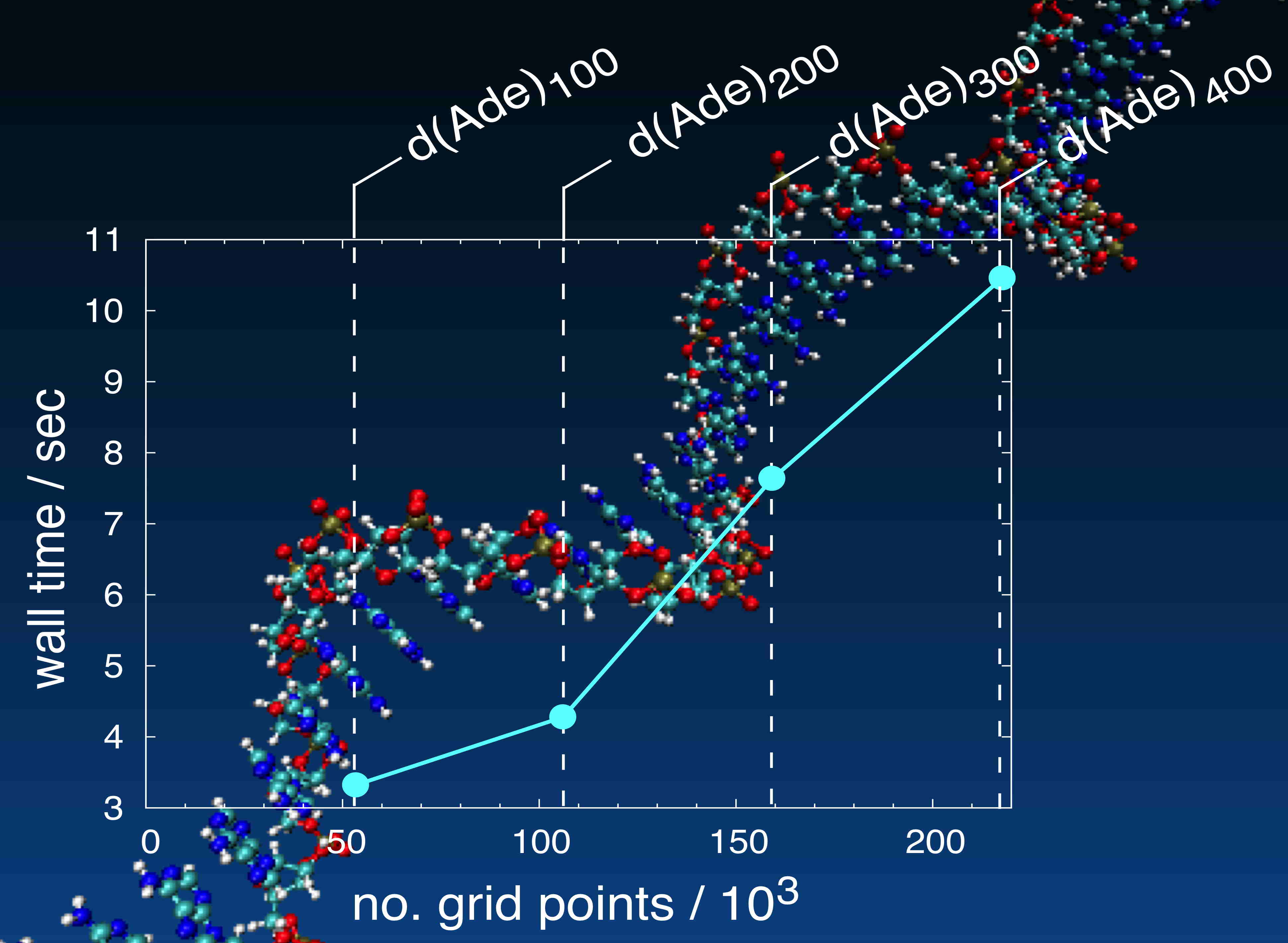
Computational scaling of MM/PCM calculations for single-stranded polyadenine, on a workstation |
PCMs are also useful in the context of QM/MM calculations, as a means to avoid costly periodic boundary conditions. Often in QM calculations, the cost of solving the PCM equations is negligible compared to the cost of calculating the wavefunction or molecular orbitals. For QM/MM and molecular mechanics (MM) calculations, however, the size of the solute cavity (and, specifically, the number of grid points necessary to discretize its surface) can become prohibitive. Our PCM implementation is highly efficient and highly parallelized, and can be used even when the solute is a large biological molecule described by an MM force field. (Computational scaling with respect to system size is shown at right.) Because the forces in our MM/PCM models are intrinsically smooth, these methods are ideally suited to molecular dynamics simulations of biological macromolecules in implicit solvent.
We have generalized the "conductor-like screening model" (COSMO), one of the most widely-used PCMs, to solutions of non-zero ionic strength. This new model, which we call the "Debye-Hückel-like screening model" (DESMO), affords an exact, numerically smooth solution of the linearized Poisson-Boltzmann equation. In other words, almost 90 years after the initial development of Debye-Hückel theory, we finally have a numerical technique that generalizes this approach to arbitrary cavity shapes. The molecules in Debye-Hückel theory need not be spherical any more!
|
|
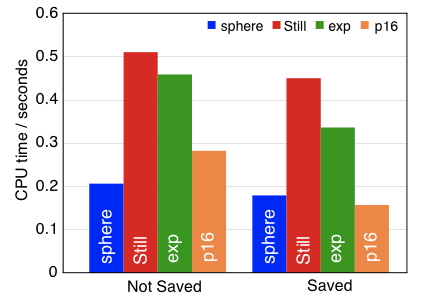
A new "p16" Coulomb operator for GB calculations is 3 times faster to evaluate than the traditional GB formulation. |
The most widely-used implicit solvent models in classical biomolecular simulations are so-called "generalized Born" (GB) models, and we have presented an analytic proof that GB models are equivalent, under reasonable assumptions, to calculations performed using the conductor-like PCM. This equivalence allows us to use PCMs to generate data sets of exact atomic pairwise-additive interaction energies for large biomolecules, and these data can be used to parameterize new GB models. Based on such tests, we have suggested a new effective Coulomb operator for GB models, which is slightly more accurate than the conventional GB operator, but is simultaneously less costly to evaluate, by as much as a factor of three.
For spectroscopic applications, a continuum solvent cannot be represented in terms of the static dielectric constant (ε0) alone, but instead should also describe how the solvent polarization changes upon excitation of the solute. Nonequilibrium PCMs have been developed for this purpose, which largely maintain the simplicity of their equilibrium counterparts but describe excited-state polarization using the solvent's optical dielectric constant (ε∞). These models can be used, for example, to compute solvatochromatic shifts in vertical excitation energies, or to describe solvent effects on vertical ionization energies. The latter quantities are increasingly being measured via liquid microjet photoelectron spectroscopy, and in the absence of continuum boundary conditions the corresponding quantum chemistry calculations can be difficult or impossible to converge with respect to the inclusion of solvent molecules. For this purpose we have developed generalized Poisson boundary conditions for quantumm chemistry calculations. These methods can also be used to describe anisotropic solvation environments, such as the air/water interface, whereas traditional PCMs are designed to describe isotropic solvation, as in the bulk liquid.