• Research
• People
• JMH Bio / CV
• Publications
• Funding
• Group meeting

Mail:
Dept. of Chemistry
Ohio State University
100 W. 18th Ave.
Columbus, OH 43210

Office:
412 CBEC

Email:
herbert@
chemistry.ohio-state.edu

John Herbert research group

Development of TD-DFT methods

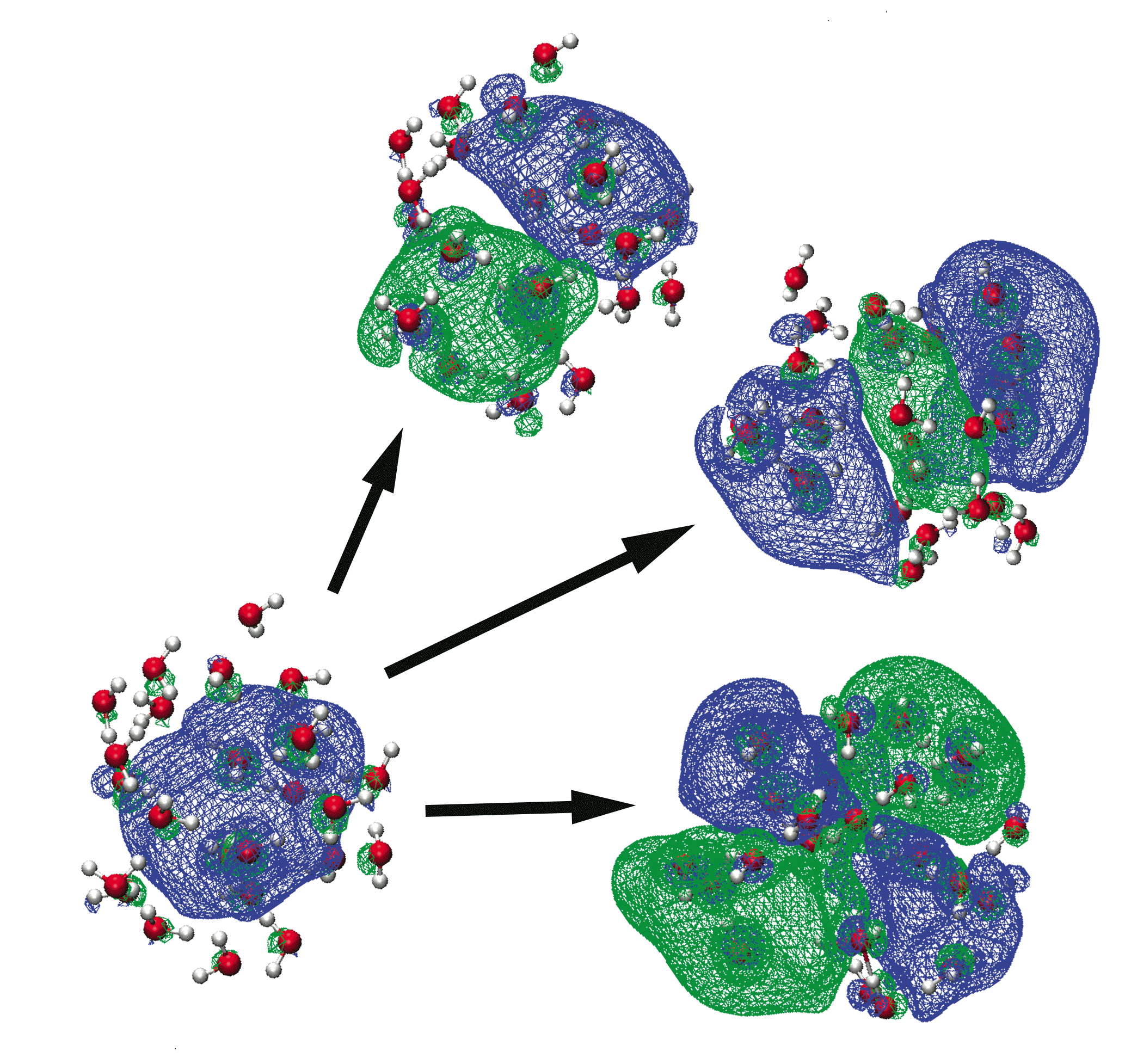
Natural transition orbitals for several electronic transitions of the aqueous electron

Overview

Time-dependent density functional theory (TD-DFT) is currently the only tractable ab initio method for calculating electronic excitation energies in systems with more than 20–30 atoms. For a wide variety of organic molecules, the (statistical) accuracy of these excitation energies is ≈ 0.3 eV (at the ground-state geometry), good enough to make the method useful in many chemistry applications. However, the high level of accuracy exhibited by TD-DFT in small-molecule calculations does not always carry over to larger systems. Moreover, the calculation of excited states in very large molecules (those containing hundreds of atoms described at the DFT level), while technically feasible, is neither trivial nor routine. QM/MM methods, with the chromophore as the QM region, are an obvious way to reduce the cost of such calculations, but sometimes very large QM regions are necessary, in order to include explicit QM solvent molecules, or to incorporate electronic coupling between multiple chromophores. Thus, we are working to extend both the computational feasibility (via improved algorithms) and the accuracy (by means of improved functionals) of large-molecule TD-DFT calculations. Much of this work is tightly integrated with other ongoing projects in our group, including the development of QM/MM methods and continuum solvation models.

We have also begun to explore the time-dependent Kohn-Sham (TDKS) method, also known as "real-time" TD-DFT, in which the Kohn-Sham analogue of the time-dependent Schrödinger equation is propagated for an out-of-equilibrium electron density created by a perturbation such as an applied laser field. The TDKS approach can describe strong-field, attosecond electron dynamics, and can also provide broad-band excitation spectra (from valence- to core-level excitations) in a single shot. So far, we have developed new propagators for the TDKS equation that facilitate longer time steps, with better numerical stability, as compared to previous approaches.

Representative Results

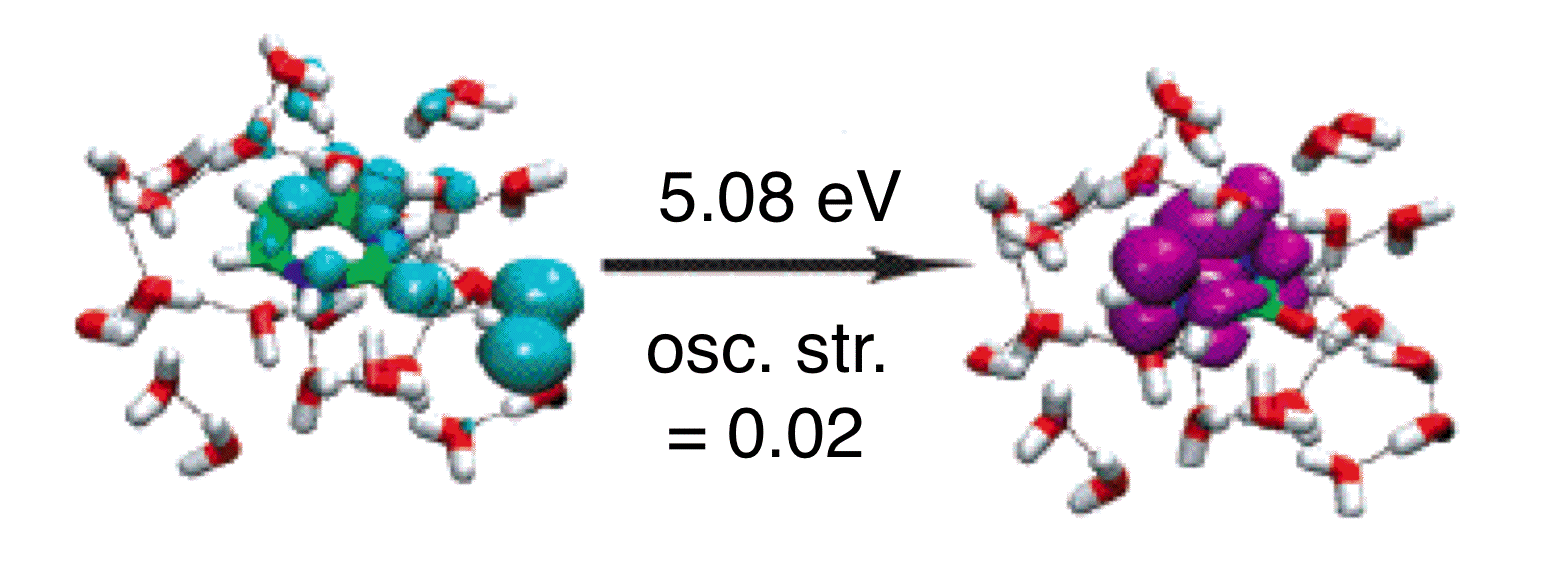
Intensity borrowing by a spurious, low-energy CT state of uracil in water, computed using TD-PBE0.

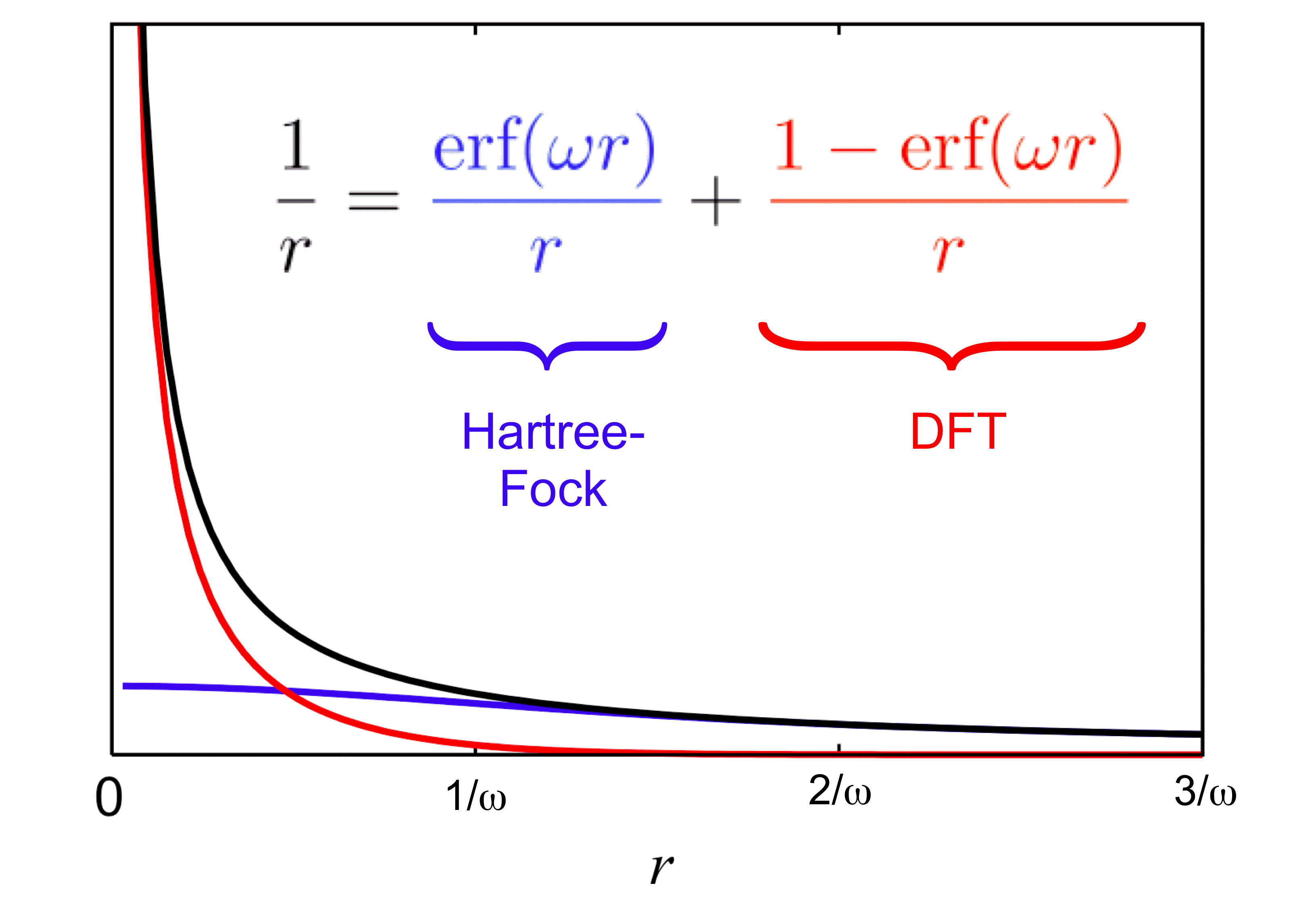
Decomposition of the Coulomb potential for LRC-DFT

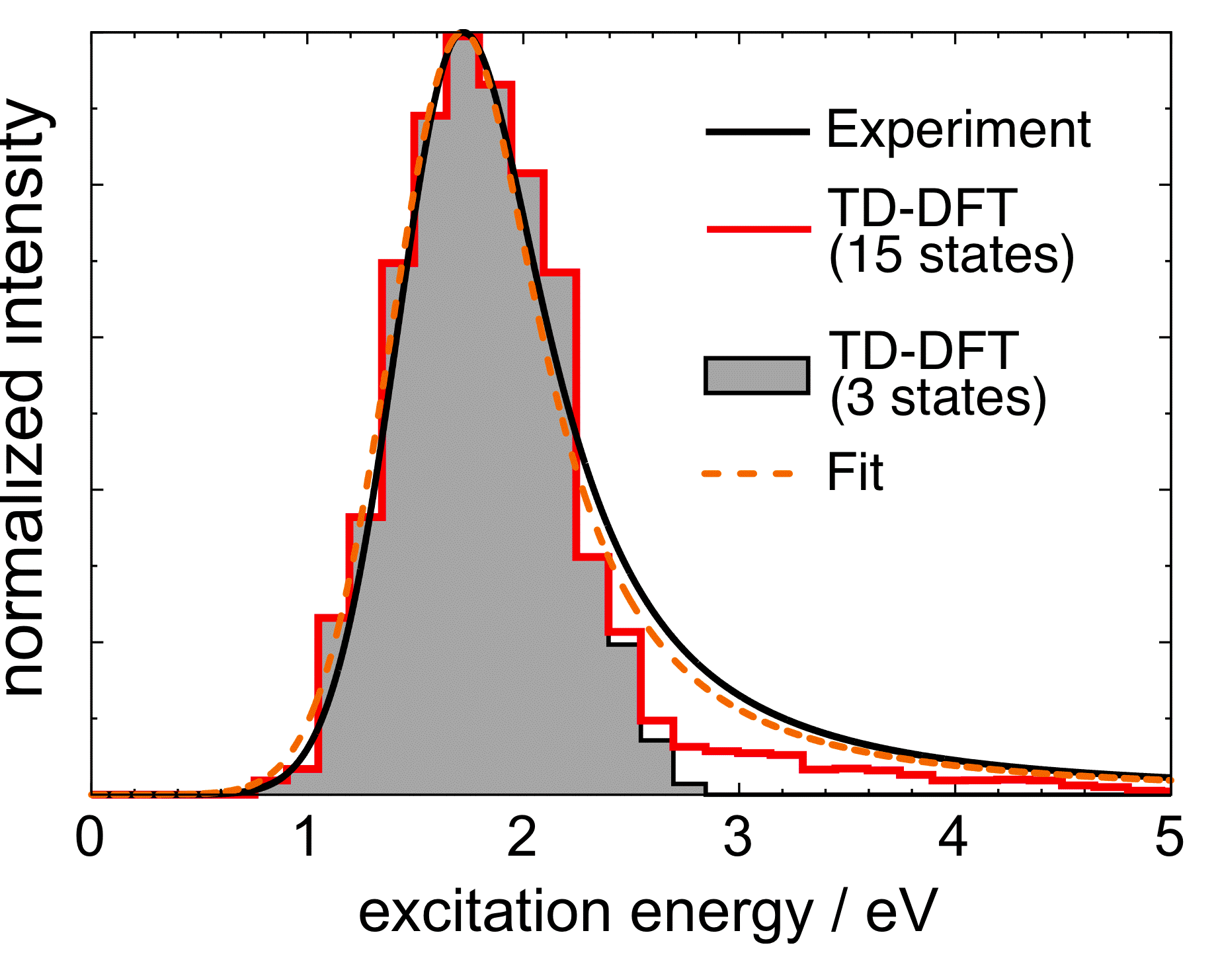
In some of our group's early work applying TD-DFT to relatively large molecules and (especially) clusters or other systems with explicit solvent molecules, we pointed out that the appearance of spurious, low-energy charge-transfer (CT) excited states is practically inevitable in large systems, when standard functionals such as BLYP, B3LYP, or PBE0 are employed. The density of spurious states grows with the size of the molecule or cluster, and these spurious states can (anomalously) borrow intensity from the real bright states. This problem is substantially ameliorated by the use of "long-range corrected" (LRC) density functionals, also known as "range-separated hybrid" functionals. The LRC approach partitions the electron-electron Coulomb operator into long- and short-range components, treating the latter with density-functional exchange, while using 100% Hartree-Fock exchange for the long-range component. These functionals have the correct asymptotic distance dependence for a charge-separated state, and thereby eliminate spurious CT states, at least in the low-energy UV region of the spectrum. As an example, we have used TD-LRC-DFT to compute the electronic absorption spectrum of the "aqueous electron", using a QM/MM model with a large QM region, and we find that the calculated spectrum is in near-quantitative agreement with experiment. Such a calculation would not have been possible using standard functionals (e.g., TD-B3LYP), because a plethora of spurious CT states would have made it prohibitively expensive to calculate enough real excited states to obtain the high-energy tail in this spectrum.

TD-LRC-DFT absorption spectrum for the aqueous electron

A variety of LRC functionals have been developed by several different research groups. We have incorporated functionals based on a short-range version of Becke '88 exchange ("μB88") and two different short-range versions of Perdew-Burke-Ernzerhof exchange ("μPBE" and "ωPBE") into Q-Chem, and have characterized their accuracy for both ground-state properties and vertical excitation energies. An important observation in these studies is that the optimal parameters for ground-state thermochemistry are often quite different from those that afford the best excitation energies, and to obtain a robust functional one must carefully balance the parameterization. The statistically-best LRC-ωPBE and LRC-ωPBEh functionals that emerged from our work are the first functionals to achieve comparable accuracy (≈ 0.3 eV) for both localized valence excitations (e.g., nπ*, ππ*, or πσ* states) as well as CT excitations. At the same time, the accuracy of ground-state predictions is not significantly degraded.

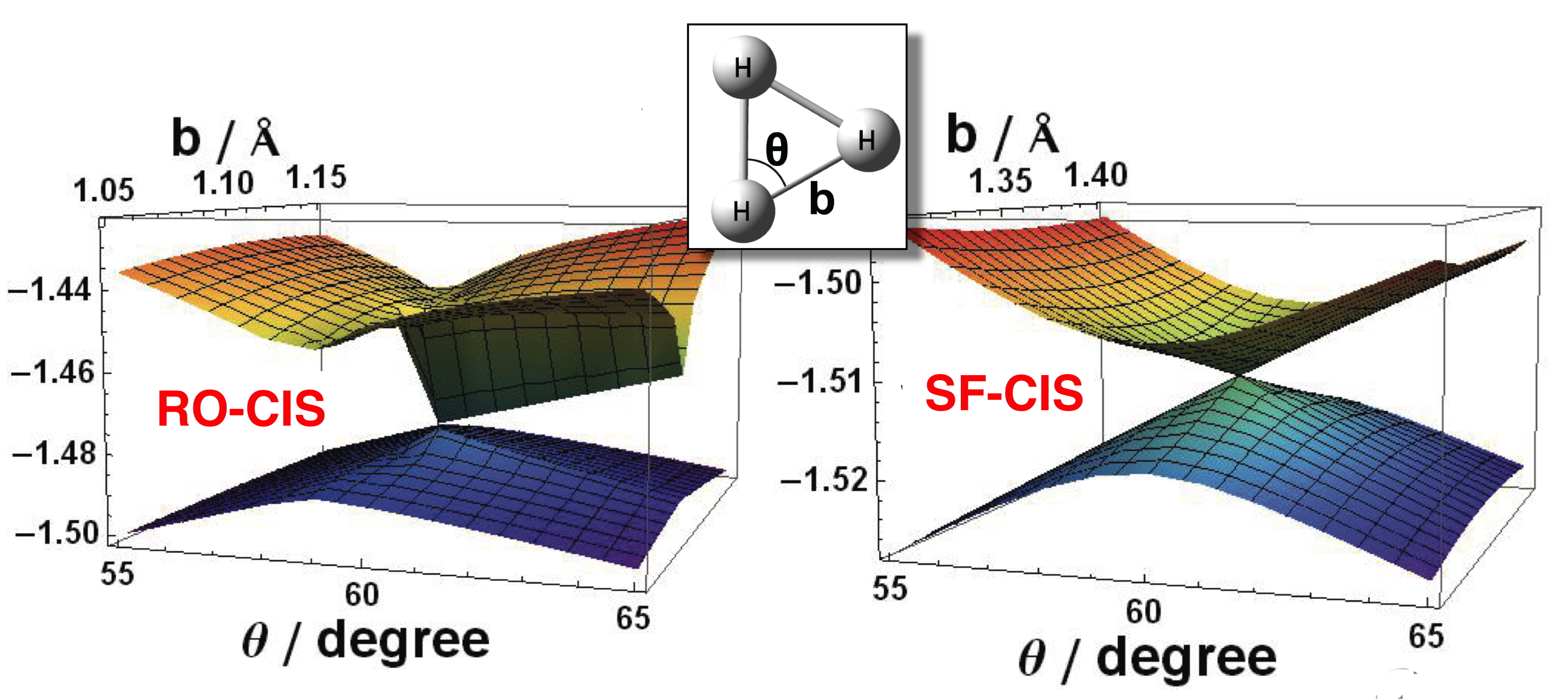
Conical intersections around the D3h degenerate ground state geometry of H3, computed using restricted open-shell CIS versus spin-flip CIS.

We have derived and implemented analytic derivative couplings for the "spin-flip" variants of configuration interaction singles (CIS) and TD-DFT. These are the couplings between excited states that are needed for nonadiabatic molecular dynamics simulations, and our algorithm allows one to perform such calculations, and to locate minimum-energy crossing points along conical seams and minimum-energy photochemical pathways, at DFT cost. Unlike derivative couplings computing using ordinary (spin-conserving) CIS or TD-DFT, spin-flip methods correctly describe the topology of the two-dimensional branching space around a conical intersection. (The example shown here is the conical intersection corresponding to the Jahn-Teller effect in the H₃ radical; in this particular case, there is a symmetry-required ground-state degeneracy, and a conical intersection that lifts the degeneracy, when the molecule has D_3h symmetry.) While H₃ is only a toy model, these methods are actively being used to understand excited-state dynamics in complex systems such as DNA. A "spin-complete" version of spin-flip TD-DFT, which resolves the spin contamination problem with that method, has also been developed.

Representative Publications

• Self-consistent predictor/corrector algorithms for stable and efficient integration of the time-dependent Kohn-Sham equation. Y. Zhu and J. M. Herbert, J. Chem. Phys. 148, 044117:1–18 (2018).


• Beyond time-dependent density functional theory using only single excitations: Methods for computational studies of excited states in complex systems. J. M. Herbert, X. Zhang, A. F. Morrison, and J. Liu, Acc. Chem. Res. 49, 931–941 (2016).


• Spin-flip, tensor equation-of-motion configuration interaction with a density-functional correction: A spin-complete method for exploring excited-state potential energy surfaces. X. Zhang and J. M. Herbert, J. Chem. Phys. 143, 234107:1–10 (2015)


• Analytic derivative couplings in time-dependent density functional theory: Quadratic response theory versus pseudo-wavefunction approach. X. Zhang and J. M. Herbert, J. Chem. Phys. 142, 064109:1–12 (2015).


• Analytic derivative couplings for spin-flip configuration interaction singles and spin-flip time-dependent density functional theory. X. Zhang and J. M. Herbert, J. Chem. Phys. 141, 064104:1–9 (2014).


• A long-range-corrected density functional that performs well for both ground-state properties and time-dependent density functional theory excitation energies, including charge-transfer excited states. M. A. Rohrdanz, K. M. Martins, and J. M. Herbert, J. Chem. Phys. 130, 054112:1–8 (2009).