
Mail:
Dept. of Chemistry & Biochemistry
The Ohio State University
151 W. Woodruff Ave.
Columbus, OH 43210
Office:
412 CBEC
Email:
herbert@
chemistry.ohio-state.edu

|
|
Schrödinger's Ket (the PI's attempt to make art) |
Research in the Herbert group is aimed at extending ab initio electronic structure theory ("quantum chemistry") to large systems. We are especially interested in condensed-phase spectroscopic experiments that probe the electronic states of molecules, radicals, and ions in aqueous solution and at the air/water interface. Interactions with the solvent, and the electronic states of the solvent itself, often play a crucial role in the interpretation of these experiments, and first-principles simulations are often needed to interpret ultrafast spectroscopic experiments with femtosecond (or even attosecond) time resolution. We have also begun to extend these "computational spectroscopy" approaches to solid-state materials such as organic photovoltaics and metal oxide photocatalysts. To facilitate these efforts, the group has developed a variety of novel low-cost electronic structure models, QM/MM methods, and continuum boundary conditions that extend quantum chemistry into the condensed phase.
To defeat the nonlinear scaling (cost versus system size) of conventional algorithms, the Herbert group is developing novel fragment-based approaches that can be understood as multiscale treatments of the electron correlation problem. Using these techniques, we are bringing wave function-based quantum chemistry methods to bear on systems of unprecedented size, e.g., to study enzymatic reaction mechanisms in much larger model systems than have previously been amenable to high-level calculations. The fragment based approach is also useful in providing an accurate description and a fundamental understanding of non-covalent interactions, with applications to supramolecular chemistry. New methods and algorithms developed in our group are incorporated into state-of-the-art quantum chemistry software packages (primarily Q-Chem) ensuring that our efforts will have a real impact on practical computational chemistry.
Recent and current projects along these lines are described below. You may also be interested in graduate study at Ohio State, in the Department of Chemistry & Biochemistry or alternatively the Chemical Physics program. The Herbert group does accept undergraduate researchers. (See also the Research Experiences for Undergraduates program.)
|
|
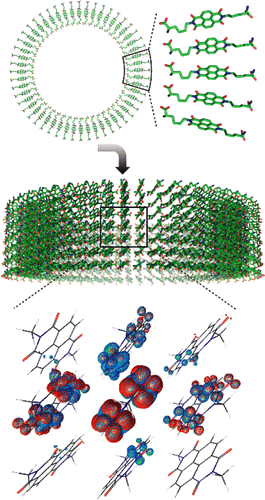
Exciton delocalization in a self-assembled nanotube |
The excited electronic states of many small chromophores are well-characterized in the gas phase, but much less is known regarding how these states are perturbed by a solvent, or by some other condensed-phase environment such as the interior of a protein. The location of conical intersections (the crucial "photochemical funnels", whose presence signifies a breakdown of the Born-Oppenheimer approximation) may be profoundly different in the condensed phase than they are in the gas phase. The Herbert group develops algorithms to explore excited-state potential energy surfaces of molecules and assemblies of molecules, as the topography and topology of these surfaces dictate the outcome of of photochemical reactions. To understand condensed-phase electronic spectroscopy at a theoretical level, it is crucial to develop low-cost methods that can include a description of the environment of the chromophore in question. This is a challenging problem for theory, because molecular excited states are inherently open-shell in nature, even if the ground state of the molecule is closed-shell, so that multireference character often cannot be ignored. New electronic structure models are needed that can describe excited states accurately, yet at a cost that is low enough to study photochemical reaction dynamics in the condensed phase.
|
|
This is a PR person's idea of what the Herbert group does. Read the (archived) article. |
Complementary to our efforts on condensed-phase photochemistry, we are also working to on better understanding of the structure of aqueous radicals and ions, in both their ground and excited electronic states, and in both bulk liquid water as well as the air/water interface. Modern ultrafast spectroscopy provides a variety of new experimental tools to probe the electronic structure of these species, and our group's goal is to develop comparable theoretical tools to understand observable spectroscopic signatures. For open-shell species in particular, there are often gaps in our knowledge of basic structure and dynamical aspects of hydration, including diffusion mechanisms, coordination numbers, and the extent to which solvent molecular orbitals contribute to the electronic structure of the radical in question. In liquid water, we have studies species such as the hydroxyl radical and the hydrated electron, e–(aq), which represent two of the most important redox-active species generated in the course of water radiolysis (i.e., the interaction of aqueous systems with ionizing radiation). Further complicating the issue is the fact that both spectroscopy and chemical reactivity can be very different at interfaces as compared to bulk solution, and the air/water interface in particular has garnered significant attention due to its role in atmospheric chemistry. A complete, molecular-level understanding of these phenomena requires not only accurate quantum mechanics (since classical force fields are often unavailable or unreliable for open-shell species) but also good statistical mechanics and simulation techniques.

|
|
"Pizza-π" model of π-stacking |
Accurate and efficient calculation of intermolecular interactions is a challenging problem for electronic structure theory. Steric repulsion and London dispersion are widely discussed intermolecular forces yet are both fundamentally quantum-mechanical in their origins, the former arising from the antisymmetry requirement (Pauli principle) and the latter from electron correlation effects that are not captured by mean-field models. The Herbert group has developed a variety of new electronic structure models to describe non-covalent interactions with quantitative accuracy yet low cost; the key is to exploit monomer wave functions as zeroth-order states and then build upon these basis states to describe the intermolecular interactions. Often we find that these approaches are comparable in accuracy to state-of-the-art CCSD(T) calculations but at a tiny fraction of the cost, and furthermore lend themselves to developing a physical rationale for the nature and strength of the intermolecular forces, by decomposing the interaction energy into physically-meaningful components (electrostatics, Pauli repulsion, polarization, dispersion, charge-transfer, etc.). We are using these methods both for accurate calculations of binding affinities in large systems (e.g., a drug molecule or other small-molecule ligand binding to a protein), but also to explore fundamental questions about the nature of non-covalent interations (e.g., what is π-stacking and how can understanding the basic molecular physics guide supramolecular synthetic chemistry?)
Fragment-based quantum chemistry methods attempt to sidestep the steep non-linear scaling of ab initio calculations by dividing a single, intractable calculation into small subsystems. This represents a physics-based (rather than a computer science-based) approach to parallelizing large-scale ab initio calculations, taking advantage of the short-range nature of quantum mechanics or what Kohn has called the "near-sightedness principle". Altneratively, one can conceptualize fragmentation methods as multiscale approaches to the electron correlation problem that attempt to use high-level quantum-mechanical techniques on short length scales, segueing to more approximate quantum mechanics methods at longer length scales and finally to classical approximations (often constructed on-the-fly from fragment wave functions), in a seamless manner. Our work on non-covalent interactions is one aspect of this, but fragmentation can be applied to macromolecular systems as well. Our group has developed a generalized many-body expansion for deriving fragment-based approximations, and shown that many other methods can be understand as particular examples of this formalism. The generalized many-body expansion helps to uncover connections between different methods, and suggests new approximations. Although many fragment-based approaches (of widely-varying accuracy and efficacy) exist, our work is aimed at systematizing these methods and turning them into black-box computational procedures ("model chemistries") that are usuable by non-experts. This is furthermore important in lending reproducibility from one research group to the next. With these methods, we aim to bring accurate, systematically-improvable quantum chemistry to applications such as enzyme reaction mechanisms.
|
|
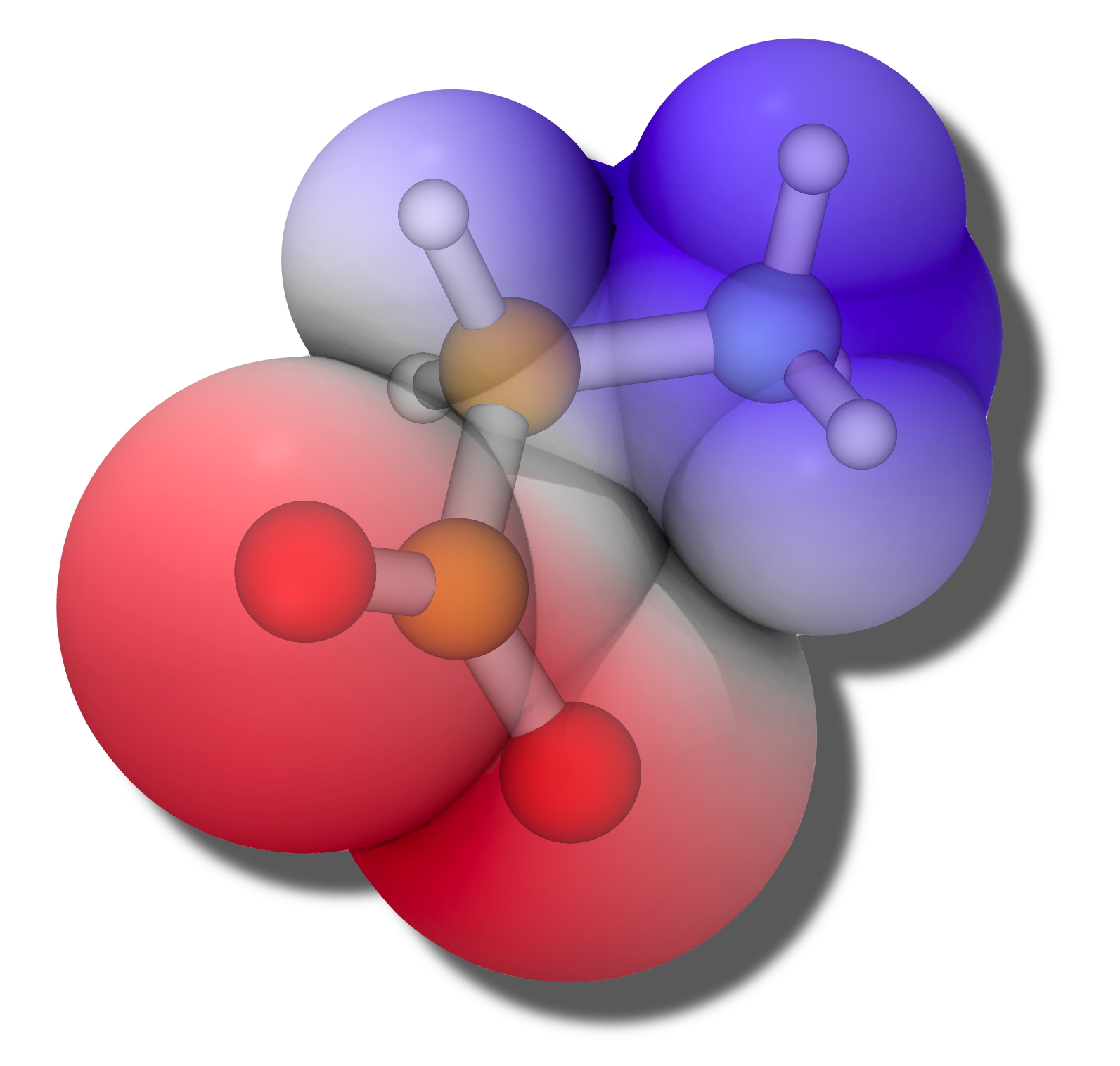
Electrostatic potential map at the solute/continuum interface |
Reaction-field solvation models, better known as polarizable continuum models (PCMs), are the most widely-used class of implicit solvent models in quantum chemistry. Given a definition for a solute cavity that defines the interface between atomistic solute and continuum solvent, these models provide an approximate solution for Poisson's equation (or the Poisson-Boltzmann equation), using relatively efficient two-dimensional surface integration, rather than the three-dimensional quadrature that is required to solve these differential equations directly. PCMs greatly accelerate conformational or phase-space sampling, since explicit solvent degrees of freedom are absent. Furthermore, as compared to empirical solvation models that are intended only to predict solvation free energies, PCMs are physically-motivated models that are directly interwoven into the system's Hamiltonian, and can thus be used to explore the effects of solvation on a variety of chemical and physical properties such as solution-phase geometries, vibrational frequencies, electronic excitation energies. We have also developed "non-equilibrium" versions of these models that describe the continuum solvent's response to excitation of the solvent, as is needed for spectroscopic applications. Anisotropic solvation models have been developed to describe the air/water interface.
|
|
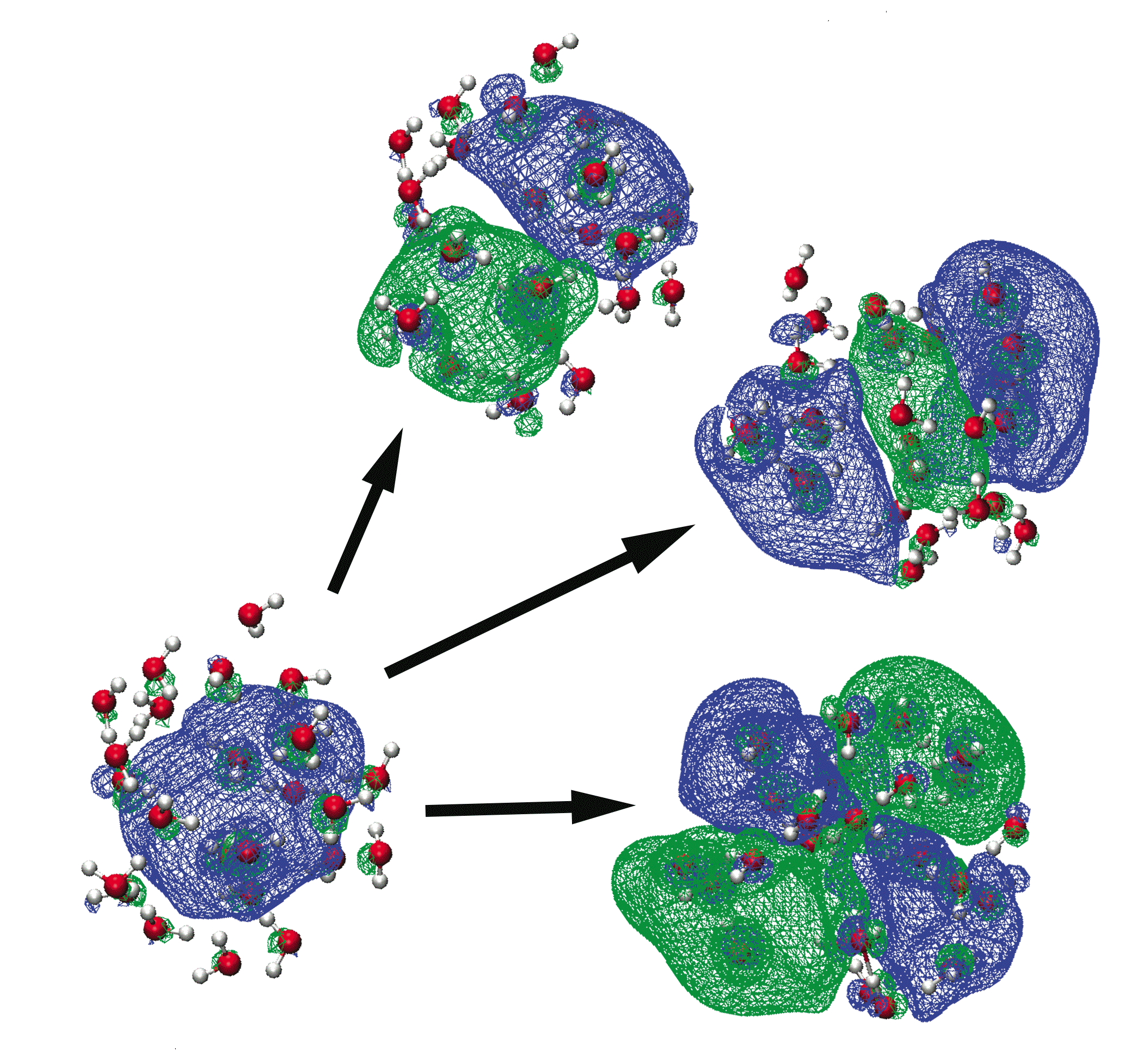
Natural transition orbitals for excited states of e–(aq) |
Time-dependent density functional theory (TD-DFT) is currently the only tractable ab initio method for calculating electronic excitation energies in systems with more than 20–30 atoms. For a wide variety of organic molecules, the (statistical) accuracy of these excitation energies is ≈ 0.3 eV (at the ground-state geometry), good enough to make the method useful in many chemistry applications. However, the high level of accuracy exhibited by TD-DFT in small-molecule calculations does not always carry over to larger systems. Moreover, the calculation of excited states in very large molecules (those containing hundreds of atoms described at the DFT level), while technically feasible, is neither trivial nor routine. QM/MM methods, with the chromophore as the QM region, are an obvious way to reduce the cost of such calculations, but sometimes very large QM regions are necessary, in order to include explicit QM solvent molecules, or to incorporate electronic coupling between multiple chromophores. Thus, we are working to extend both the computational feasibility (via improved algorithms) and the accuracy (by means of improved functionals) of large-molecule TD-DFT calculations. Much of this work is tightly integrated with other ongoing projects in our group, including the development of QM/MM methods and continuum solvation models.
|
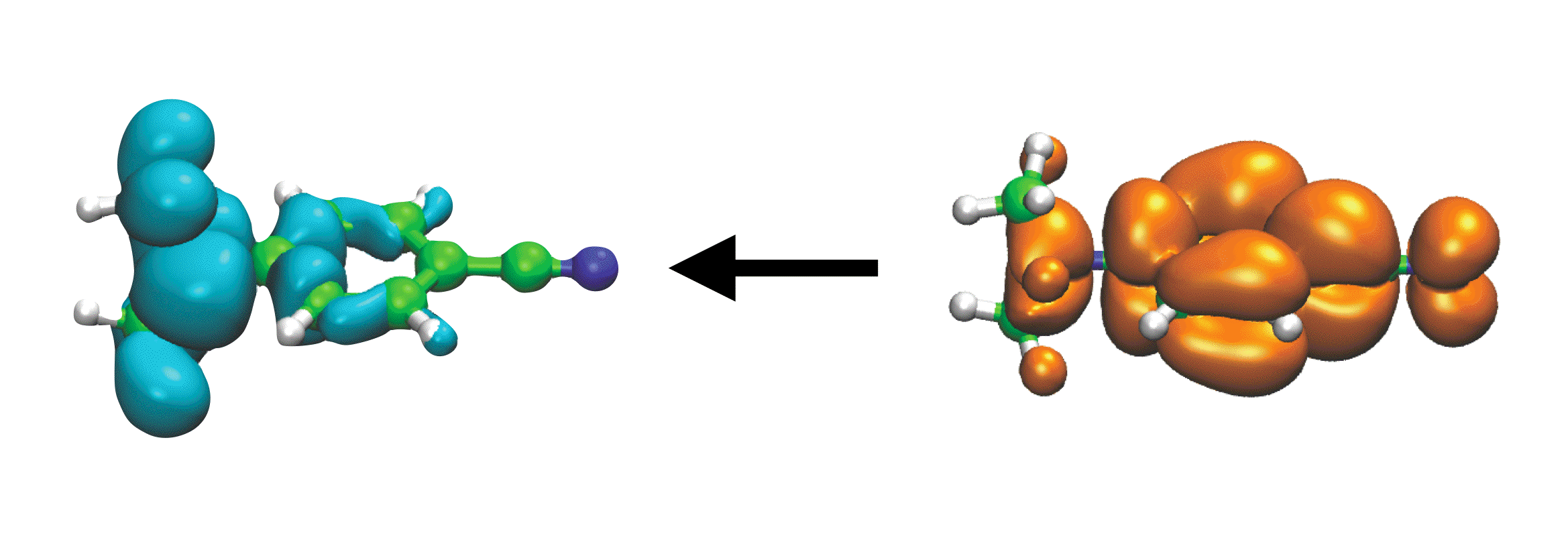
|
S0 ← S1 emission in the DMABN molecule, which exhibits intramolecular CT character |
Electronic excitation is characterized by an instantaneous (possibly drastic) change in the electron density of the molecular or functional group that absorbs the photon. In particular, intramolecular charge-transfer excited states such as those present in "donor-π-acceptor" or "push-pull" chromophores, can change the dipole moment of the chromophore by 10 Debye or more. In a condensed-phase environment, a proper description of such an event should allow the electronic degrees of freedom of the environment to remain in equilibrium with those of the chromophore, i.e., the chromophore and its environment should polarize one another in a self-consistent fashion. In addition, the most accurate molecular mechanics (MM) force fields are often polarizable ones. In the context of QM/MM calculations, the increased cost associated with using a polarizable force field should be insignificant, provided that the QM/MM algorithm is designed in a reasonable way. We are developing computationally-efficient QM/MM models that utilize polarizable MM force fields ("QM/polMM" models), in an effort to describe excited states in solution. We aim for solvation models that are accurate across the entire range of system sizes, from small clusters to bulk solvation. These new methods enable us to explore the role of solvent polarization, which is especially important for the description of charge-separated excited states, and to make contact with both condensed-phase electronic spectroscopy, as well as gas-phase cluster experiments.
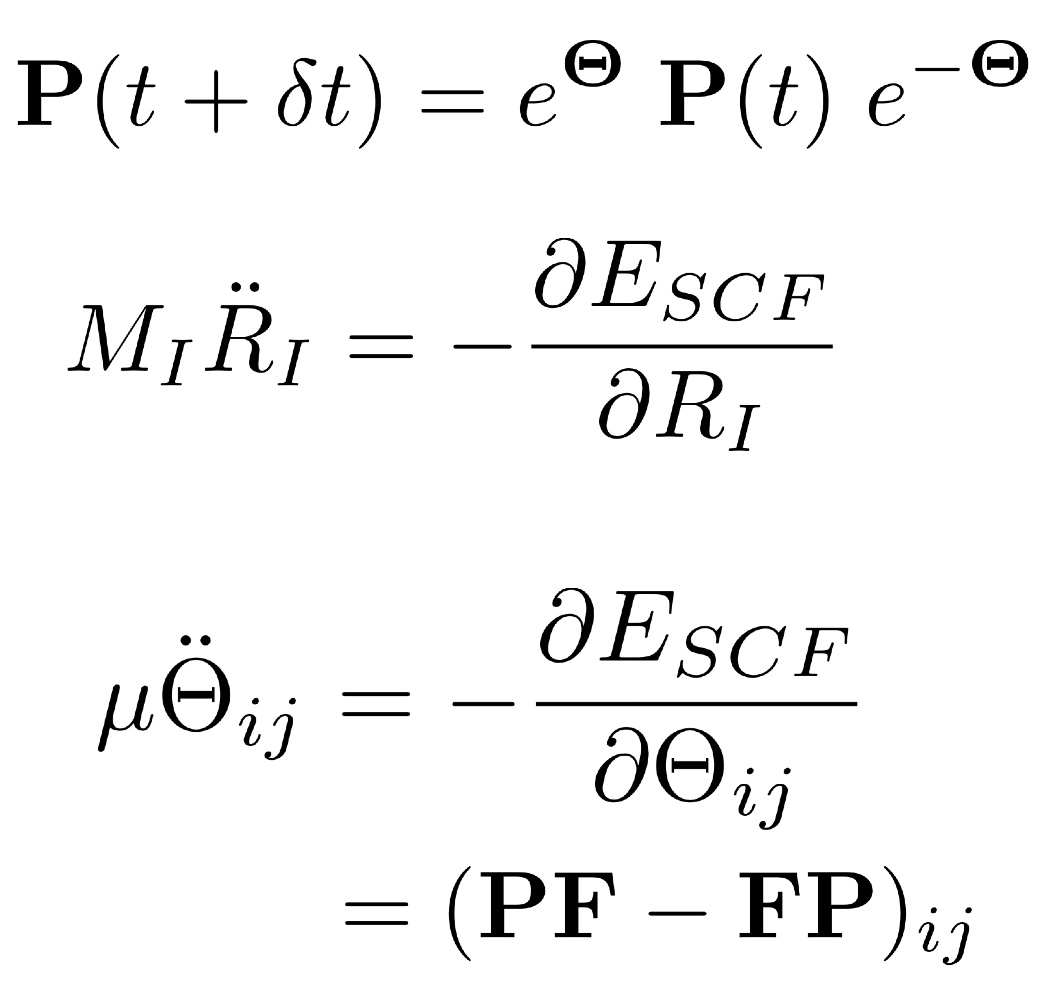
|
|
Equations of motion for extended- Lagrangian ab initio molecular dynamics. |
Efficient algorithms developed in our group are expanding the frontiers of ab initio molecular dynamics (AIMD) simulations, in which on-the-fly quantum chemistry (i.e., a quantum-mechanical treatment of the electrons) is used to calculate the forces required for a classical molecular dynamics simulation, thus obviating the need for parametrized force fields. This is especially important for unusual or reactive species (such as the hydrated electron and other aqueous radicals), for which it is extremely difficult to construct accurate force fields. Improvements to the efficiency of AIMD algorithms translate directly into longer simulation time scales and larger system sizes, for a fixed quantity of computer resources.

|
Our group contributes to the development of Q-Chem, a state-of-the-art electronic structure program package. (See also IQMol, a structure builder and graphical front-end for Q-Chem.) Group members have the opportunity to become co-authors of future versions of the software. A stand-alone code, Fragme∩t, is also developed in our group, for performing fragment-based quantum chemistry calculations with interfaces to various quantum chemistry software packages.
Last modified 11 November, 2020. Proudly powered by Words. By which we mean, hand-written HTML.