King-Yeung Lam (Adrian)
Site Navigation

Submitted Articles/Preprints:
|
R.S. Cantrell, C. Cosner, K.-Y. Lam and H. Zhang, Ideal Free Distribution in a Multiple Predator-prey System, submitted to Bull. Math. Biol., Special Issue in memory of Mary Ann Horn.
We study the mechanism and effects of ideal free distributions (IFDs) on an ecological community consisting of $n$ prey and $m$ predator species, for any positive integers $n$ and $m$, by considering the corresponding diffusive Lotka-Volterra system with time-periodic coefficients. We define a notion of joint IFD in a time-periodic environment, and give necessary and sufficient conditions for it to be achieved by a subcollection of prey and predator species with suitable dispersal strategies. Next, we show, via construction of a Lyapunov function, that such dispersal strategies are evolutionarily stable, in the sense that if a subcollection of prey and predator species adopts an ideal free dispersal strategy, then the total community must converge to an IFD for large time; if a unique combination of prey-predator species adopts an ideal free strategy, then it can {drive} all other species to extinction. Conversely, if a combination of prey-predator species adopts a non-ideal free dispersal strategy, then it can be invaded by some suitable mutant strategies.
Our results provide insight into the evolution of spatial distribution of ecological communities with predator-prey interactions.
|
||
|
J.-W. Chu, K.-Y. Lam and Z.-A. Wang, Global dynamics of a diffusive population-toxicant model with toxicant-taxis in time-periodic environments, preprint.
This paper {investigates} a population-toxicant system incorporating the ability of population to avoid toxicants (i.e., toxicant-taxis) in polluted aquatic environments, where the toxicant input rate exhibits spatial heterogeneity and temporal periodicity. Unlike the monotone dynamical system recently studied by Li and Wang \cite{LiZZ-2024-submitted}, which lacks the toxicant-taxis, our quasilinear system is not order-preserving. Consequently, the asymptotic theory for monotone dynamical systems and the comparison principle are inapplicable. To address these difficulties, we employ the principal Floquet bundle theory and uniform persistence theory to establish the existence of positive periodic solutions and uniform persistence. {We further apply the energy method to study the global stability of semi-trivial and positive time-periodic solutions under specific conditions. Via} subsolution construction and Sard's theorem, we prove that strong toxicant-taxis destabilizes the semi-trivial time-periodic solution and expands the parameter range of uniform persistence in heterogeneous environments. Finally, numerical simulations are conducted to extend our theoretical results. {Our findings show that if the toxicant-induced death rate is high (resp. low), then the species goes extinct (resp. persists); when the toxicant-induced death rate is moderate, both extinction and persistence may be stable (i.e., bi-stability). We also find that the ability of toxicant-avoidance, even if not strong, can enhance the survival of aquatic species in polluted environments.
|
||
|
(with L. Wang and F. Lutscher) Evolution of movement strategies in patchy landscapes, submitted.
|
||
|
(with C.-H. Wu) On the logarithmic correction of transition fronts in shifting environments, submitted.
(DOI arXiv:2509.11521).
|
|
Research Monograph:
| 1 |
K.-Y. Lam and Y. Lou,
Introduction to Reaction-Diffusion Equations: Theory and Applications to Spatial Ecology and Evolutionary Biology, in press with Springer Cham, December 2022, 324pp.
(Link to Springer.com)
Table of Contents[Part I Linear Theory] 1. The maximum principle and principal eigenvalue for single equations; 2. The principal eigenvalue for periodic-parabolic problems ; 3. The maximum principle and principal eigenvalue for systems; 4. The principal Floquet bundle for parabolice quations;  |
Chap.1 |
| 16 |
I. Averill, K.-Y. Lam and Y. Lou,
The role of advection in a two-species competition model: a bifurcation approach,
Mem. Amer. Math. Soc., Vol. 245 (2017), no. 1161, v+117pp.
(DOI 10.1090/memo/1161)  
 Read abstractThe effects of weak and strong advection on the dynamics of reaction- diffusion models have long been studied. In contrast, the role of intermediate advec- tion remains poorly understood. For example, concentration phenomena can occur when advection is strong, providing a mechanism for the coexistence of multiple populations, in contrast with the situation of weak advection where coexistence may not be possible. The transition of the dynamics from weak to strong advection is generally difficult to determine. In this work we consider a mathematical model of two competing populations in a spatially varying but temporally constant environment, where both species have the same population dynamics but different dispersal strategies: one species adopts random dispersal, while the dispersal strategy for the other species is a combination of random dispersal and advection upward along the resource gradient. For any given diffusion rates we consider the bifurcation diagram of positive steady states by using the advection rate as the bifurcation parameter. This approach enables us to capture the change of dynamics from weak advection to strong advection. We will determine three different types of bifurcation diagrams, depending on the difference of diffusion rates. Some exact multiplicity results about bifurcation points will also be presented. Our results can unify some previous work and, as a case study about the role of advection, also contribute to our understanding of intermediate (relative to diffusion) advection in reaction-diffusion models. |
Book Chapter / Survey Articles:
| 3 |
K.-Y. Lam, Getting Your Hands Dirty: Teaching Math Biology with Active Learning Strategies. Early Career Section,
Bull. Amer. Math. Soc., Vol. 41, No. 4, April 2024, pp. 10-12.
(DOI 10.1090/noti2916).
|
|
| 2 |
K.-Y. Lam, S. Liu, and Y. Lou, Selected topics on reaction-diffusion-advection models from spatial ecology.
Math. Appl. Sci. Eng., Vol. 1 No. 2 (2020): pp. 91-206.
(DOI 10.5206/mase/10644).
We discuss the effects of movement and spatial heterogeneity on population dynamics via reaction–diffusion-advection models, focusing on the persistence, competition, and evolution of organisms in spatially heterogeneous environments. Topics include Lokta-Volterra competition models, river models, evolution of biased movement, phytoplanktongrowth, and spatial spread of epidemic disease. Open problems and conjectures are presented.P arts of this survey are adopted from the materials in [89,108,109], and some very recent progress are also included.
|
|
| 1 |
K.-Y. Lam and Y. Lou,
Persistence, Competition, and Evolution.
In: Bianchi A., Hillen T., Lewis M., Yi Y. (eds) The Dynamics of Biological Systems.
Mathematics of Planet Earth, vol 4. Springer, Cham (2020) 31pp. (DOI 10.1007/978-3-030-22583-4_8). Read abstractIn this chapter we discuss some reaction-diffusion models for the persistence of a single species, the competition of two populations, and the evolution of dispersal in spatially heterogeneous environments and advective environments. Our goal is to illustrate some interesting, and perhaps surprising, effects of spatial heterogeneity and diffusion on the population dynamics. Specific topics include the logistic model, linear eigenvalue problem with indefinite weight, Lotka-Volterra competition models, reaction-diffusion models in advective environments, and the evolution of dispersal.chrome://bookmarks/ We will introduce some basic tools for reaction-diffusion equations such as the super-sub solution method, the variational principle for principle eigenvalues, Lyapunov functionals, comparison principles for parabolic equations and systems, etc. Some recent developments will be discussed. In addition, problems with various difficulties ranging from elementary exercises to open research questions will be presented. |
|
| 66 |
C. Henderson and
K.-Y. Lam, A Hamilton-Jacobi approach to road-field reaction-diffusion models,
J. Math. Pures Appl., Vol. 205 (2026), 103798, 65pp.
(Note on comaprison principle.)(DOI 10.1016/j.matpur.2025.103798 with open access).
We consider the road-field reaction-diffusion model introduced by Berestycki, Roquejoffre, and Rossi. By performing a “thin-front limit,” we are able to deduce a Hamilton-Jacobi equation with a suitable effective Hamiltonian on the road that governs the front location of the road-field model. Our main motivation is to apply the theory of strong (flux-limited) viscosity solutions in order to determine a control formulation interpretation of the front location. In view of the ecological meaning of the road-field model, this is natural as it casts the invasion problem as one of finding optimal paths that balance the positive growth rate in the field with the fast diffusion on the road. Our main contribution is a nearly complete picture of the behavior on two-road conical domains. When the diffusivities on each road are the same, we show that the propagation speed in each direction in the cone can be computed via those associated with one-road half-space problem. When the diffusivities differ, we show that the speed along the faster road is unchanged, while the speed along the slower road can be enhanced. Along the way we provide a new proof of known results on the one-road half-space problem via our approach. |
|
| 66 |
K.-Y. Lam and H. Zhang, Ideal free distribution of multiple species
in a time-periodic and patchy habitat, online first, CSIAM Trans. Life Sci. (2025), 21pp.
(DOI 10.4208/csiam-ls.SO-2025-0019).
(journal site).
Dispersal strategies that can produce ideal free distribution (IFD) have been shown to be evolutionarily stable in various ecological models.
In this paper, we investigate this phenomenon through a time-periodic patch model, where $N$ species have identical ecological dynamics but distinct dispersal strategies.
We extend the concept of IFD, or joint IFD, previously established in temporally constant or temporally periodic but spatially continuous environments, to time-periodic patch environments and derive a sufficient and necessary condition for IFD to be feasible.
Under this condition, we demonstrate two competitive advantages of ideal free dispersal strategies: when a subset of species adopts an ideal free dispersal strategy, the solution of the initial value problem must converges to an IFD; if a unique species combination achieves a joint IFD, then this subset will dominate and competitively exclude the other species.
Furthermore, we show that ideal free dispersal strategies are the only evolutionarily stable strategies.
Our results extend previous work to competitive models of multiple species via construction of suitable Lyapunov functions in time-periodic setting.
|
|
| 64 |
K.-Y. Lam, D. Tang and Z.-A. Wang, Existence of positive steady-state solutions to the SKT competition system with cross-diffusion. 33pp., SIAM J. Math, Anal., available online (2025).
(DOI: 10.1137/24M1700284)
Highlights: We study the case (iii) limiting system of the stationary Shigesada-Kawasaki-Teramoto competition system with cross-diffusion, obtained in Lou and Ni in 1999.
This paper is concerned with the following stationary Shigesada-Kawasaki-Teramoto competition system with cross-diffusion, by studying the limiting system obtained as case (iii) in Lou and Ni in 1999.
In this paper, we establish the existence/nonexistence of non-constant positive solutions, which fills some gaps left out in the existing results. First, we show there are no positive solutions in the case of strong-weak competition, for large $\mu>0$. Then, by studying the shadow system of the above system as $\mu\to\infty$, we establish the existence of positive solutions for large $\mu>0$ in other various ranges of $b,c>0$ including all possible competitions: weak, strong-weak and strong. In particular, we find some conditions under which multiple positive solutions exist. Then we show the existence of positive solutions for some $\mu>0$ in the case of weak competition.
|
|
| 63 |
K.-Y. Lam, G. Nadin and X. Yu, Asymptotic spreading of KPP reactive fronts in heterogeneous shifting environments II: Flux-limited solutions,
Math. Ann., Volume 392, pages 5429–5481, (2025).
(DOI 10.1007/s00208-025-03222-6).
Highlights: We study the Fisher-KPP equation with coefficient of the form g(x-ct), where g is nonmonotone, and establish the connection with flux-limited viscosity solution of the limiting Hamilton-Jacobi equations.  
We consider the spreading dynamics of the Fisher-KPP equation in a shifting environment, by analyzing the limit of the rate function of the solutions. For environments with a weak monotone condition, it was demonstrated in a previous paper that the rate function converges to the unique Ishii solution of the underlying Hamilton-Jacobi equations. In case the environment does not satisfy the weak monotone condition, we show that the rate function is then characterized by the Hamilton-Jacobi equation with a dynamic junction condition, which depends additionally on the generalized eigenvalue derived from the environmental function. Our results applies to the case when the environment has multiple shifting speeds, and clarify the connection with previous results on nonlocally pulled fronts and forced traveling waves.
|
|
| 62 |
(With C. Cosner, RS. Cantrell, and I. Mazari) Mean field game and the ideal free distribution, J. Biol. Math.,
91, 46 (2025).
Topical Collection to celebrate 50 years of JOMB. (DOI 10.1007/s00285-025-02276-z).
|
|
| 61 |
Jiawei Chu,
K.-Y. Lam, Boyu Wang and Tong Wang, An optimal switching approach for bird migration,
accepted, Numer. Algebra Control Optim., Special issue ``Mathematical Biology, Differential Equations, and Optimal Control: In honor of Suzanne Lenhart on her 70th birthday", 36pp.
(DOI 10.3934/naco.2025026).
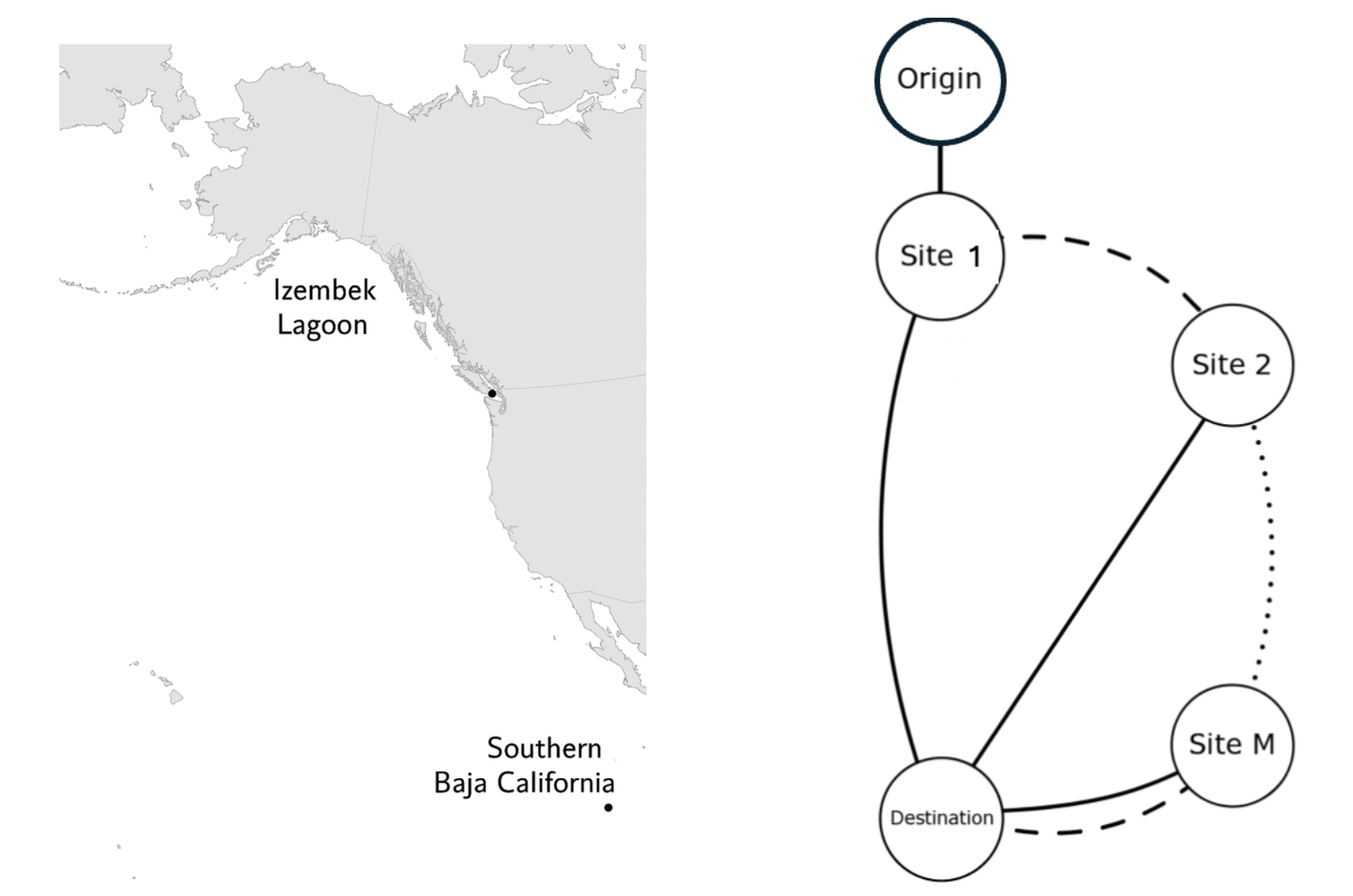
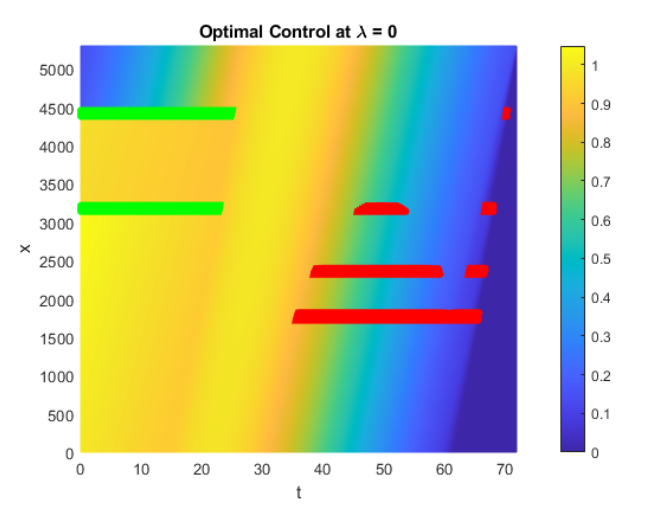
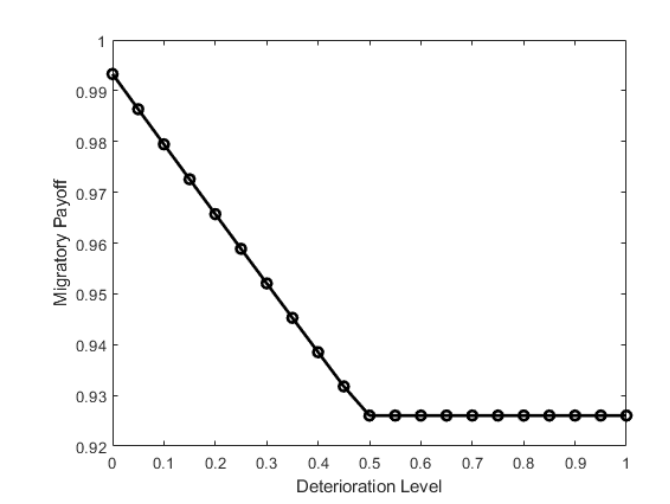
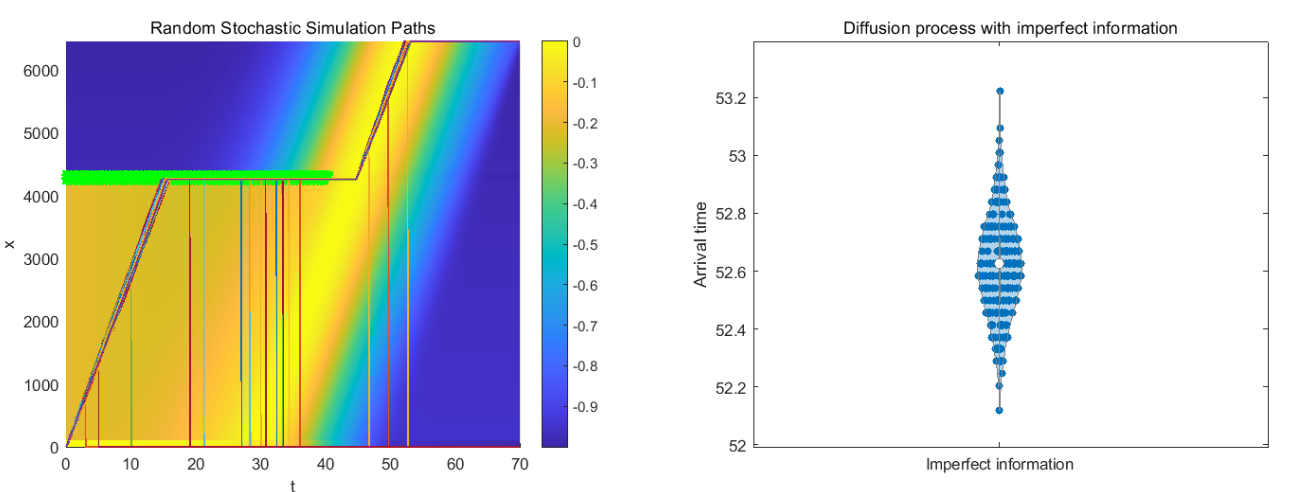
Bird migration is an adaptive behavior ultimately aiming at optimizing survival and reproductive success. We propose an optimal switching model to study bird migration, where birds' migration behaviors can be efficiently modeled as switching between different stochastic differential equations. For individuals with perfect information regarding the environment, we implement numeric methods to see the expected payoff and corresponding optimal control. For individual with only partial information of the environment, we combine the finite difference method and stochastic simulations to investigate the change of the bird's optimal strategy. Based on biological backgrounds, we characterizing the optimal strategies of birds under different scenarios and these behaviors depend on the specific assumptions of the model.
|
|
| 60 |
H. Jin, K.-Y. Lam and Z.-A. Wang, Global dynamics of the toxicant-taxis model with Robin boundary
conditions, Calc. Var. Partial Differ. Equ.,Volume 64, article number 270, (2025), 40pp. (With open access)
(DOI 10.1007/s00526-025-03105-3).
|
|
| 59 |
Baragary, Ashley; Wang, Lin; Lam, Adrian; Ali, Arwa; Belden, Jason; Collins, Kevin; Zhang, Bo, Determining the optimal movement strategies in environments with heterogeneously distributed resource and toxicant, OIKOS, 2025: e10962.
(DOI 10.1111/oik.10962).
Highlights: We study the optimal dispersal rate in heterogeneous food and heterogeneous toxin via the C. elegans experiment. 
|
|
| 58 |
J. Jacobs, Y. Salmaniw, K.-Y. Lam, L. Zhai, H Wang and B. Zhang,
Fundamental principles of the effect of habitat fragmentation on species with different movement rates,
Conservation Biology,
(2024), accepted.
(DOI 10.1111/cobi.14424).
Highlights: We define a fragmentation index for a given patchy environment in 2d by analyzing the effective growth rate of randomly diffusing organisms in such an environment. 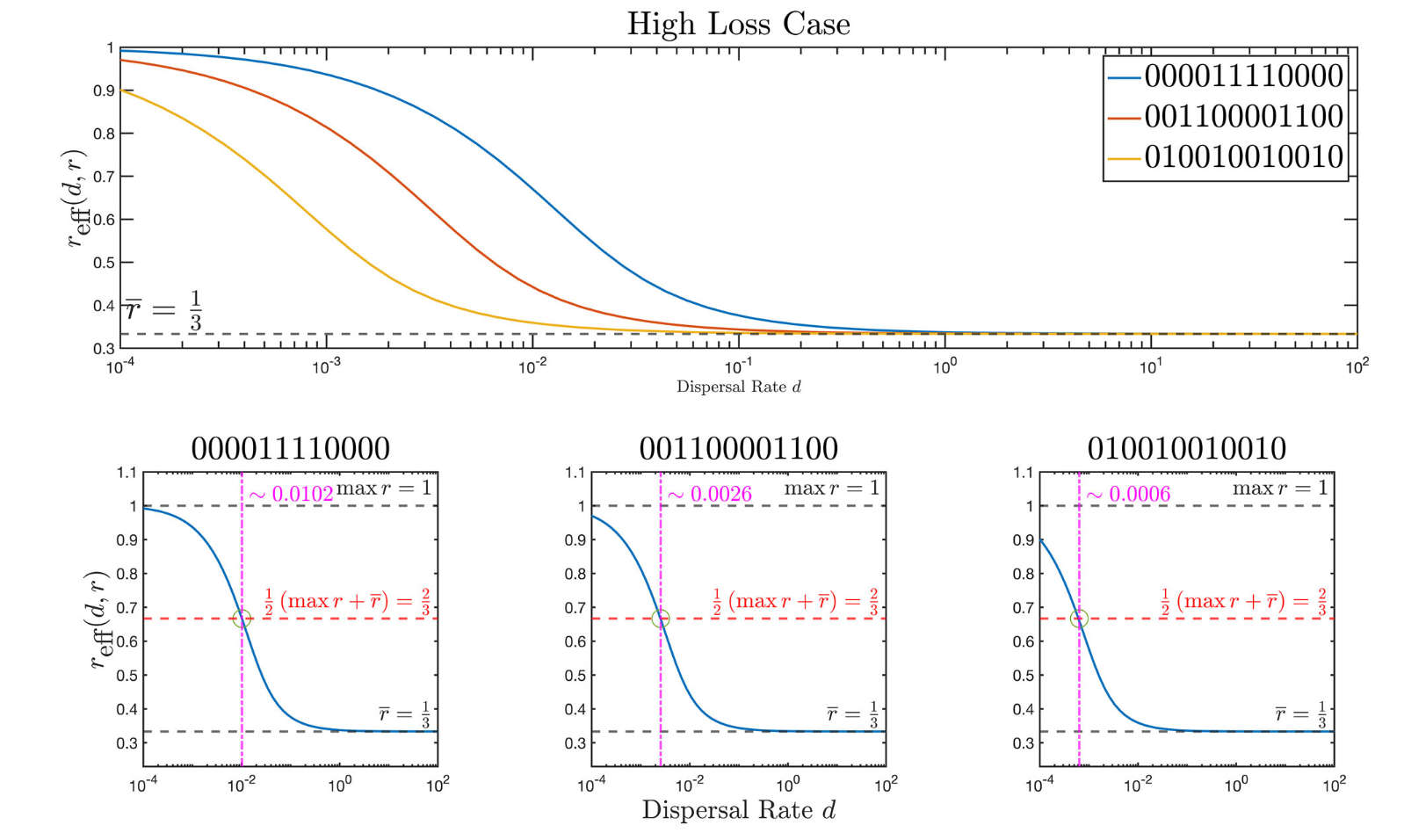 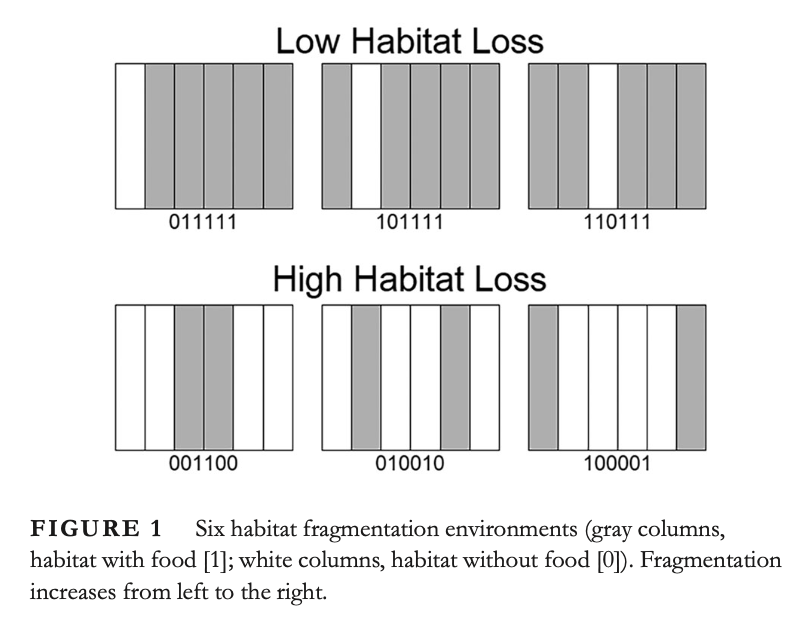
|
|
| 57 |
L. Wang, K.-Y. Lam, B. Zhang,
On the principal eigenvalue of cooperative elliptic systems with applications to a population model with two reversible states,
Disc. Contin. Dyn. Syst. Ser. B,
(2025), Volume 30, Issue 7: 2306-2325.
(DOI 10.3934/dcdsb.2024166).
Highlights: This is the mathematical paper (companion to Baragary et al.) studying the effect of joint resource/toxin distribution on effective growth rate. We show that spatial heterogeneity alone can select for higher dispersal.
We prove novel monotonic results of cooperative elliptic eigenvalue problems on a bounded one-dimensional domain under suitable conditions, which are then applied to analyze a population model with state-switching. Our results demonstrate that spatial heterogeneity alone can lead to selection of higher movement rate, which implies that the reduction phenomenon due to [L. Altenberg, Proc. Nat. Acad. Sci. (2012)] fails for general elliptic cooperative systems. This also provides a plausible mechanism for the differing effective growth rates of the high and low movement strains in different spatial placement of nutrients and toxins, as observed in recent biological experiments involving nematode populations.
|
|
| 56 |
K.-Y. Lam, X.-Q. Zhao and M. Zhu, Global dynamics of reaction-diffusion systems with a time-varying domain,
SIAM J. Appl. Math.,
84 no. 4 (2024), pp. 1742-1765.
(DOI 10.1137/23M1582990).
Highlights: Prof. XQ Zhao asked me a question that was left open in this unfinished paper at a workshop at Fields Institute in celebration of Mark Lewis' 60th birthday, and we occupied ourselves with a lot of note swapping during the workshop and after. Afterwards, they graciously added me to the list of authors.
This paper is devoted to the study of the global dynamics for a large class of reaction-diffusion systems with a time-varying domain. By appealing to the theories of asymptotically autonomous and periodic semiflows, we establish the threshold-type results on the long-time behavior of solutions for such a system in the cases of asymptotically bounded and periodic domains, respectively. To investigate the model system in the case of asymptotically unbounded domain, wefirst prove the global attractivity for nonautonomous reaction-diffusion systems with asymptotically vanishing diffusion coefficients via the method of sub- and supersolutions and then use the comparison arguments to obtain the threshold dynamics. We also apply these analytical results to a reaction-diffusion model of dengue fever transmission to investigate the effect of time-varying domain on the basic reproduction number. It turns out that the basic reproduction numbers with dengue fever transmission for the asymptotically bounded and unbounded domains are always less than that for the spatially homogeneous case, and under appropriate conditions, the basic reproduction numbers for asymptotically bounded and periodic domains are larger than or equal to that for the stationary bounded domain.
|
|
| 55 |
Qing Li, Xinfu Chen,
K.-Y. Lam and Yaping Wu, Propagation phenomena for a nonlocal reaction-diffusion model with bounded phenotypic traits,
J. Differential Equations
411 (2024) pp. 794-822.
(DOI 10.2139/ssrn.4786342).
Highlights: This happened with a workshop in celebration of Prof Xuefeng Wang's 60th birthday at Chern Institute at Tianjin, China. Prof. Yaping Wu invited me to join this exploration of propagation in a cylinder domain, and it helped me understand better the arguments of Hamel et al. concerning a PDE argument to prove logarithmic delay that was originally due to M. Bramson.
In this paper we study the stability of cylinder front waves and propagation of solution for a nonlocal Fisher type model describing the segregation of a population with nonlocal competition among bounded and continuous phenotypic traits. By applying spectral analysis and separation of variables, we first prove the spectral and local exponential stability of cylinder waves with noncritical speeds in some exponentially weighted spaces. By applying detailed analysis with spectral expansion and special sub-super solution construction, we further prove the uniform boundedness of solution and global asymptotic stability of waves for more general nonnegative initial value, and prove that the spreading speed and asymptotic behavior of solution are determined by the decay rate of initial value, which also extends some classical results on the stability of planar waves for Fisher-KPP equation to the nonlocal Fisher model in multi-dimensional cylinder setting.
|
|
| 54 |
K.-Y. Lam and Ray Lee, Asymptotic spreading of predator-prey populations in a shifting environment,
Mathematics in Applied Sciences and Engineering, Vol. 5 No. 3 (2024), pp. 185-275.
(DOI 10.5206/mase/18029).
Inspired by recent studies associating shifting temperature conditions with changes in the efficiency of predator species in converting their prey to offspring, we propose a predator-prey model of reaction-diffusion type to analyze the consequence of such effects on the population dynamics and spread of species. In the model, the predator conversion efficiency is represented by a spatially heterogeneous function depending on the variable ξ=x−c1t for some given c1>0. Using the Hamilton-Jacobi approach, we provide explicit formulas for the spreading speed of the predator species. When the conversion function is monotone increasing, the spreading speed is determined in all cases and non-local pulling is possible. When the function is monotone decreasing, we provide formulas for the spreading speed when the rate of shift of the conversion function is sufficiently fast or slow.
|
|
| 53 |
K.-Y. Lam and Y. Lou,
The principal Floquet bundle and the dynamics of fast diffusing communities, Trans. Amer. Math. Soc., 377 (2024), 1-29.
(DOI: 10.1090/tran/8975).
Highlights: We obtain progress on the conjecture of Dockery et al concerning competition of N species which are identical except for their diffusion rate. We obtained expansion of Floquet bundle (of linear parabolic equations) in fast diffusion rate, which is of independent interest. Read abstractFor $N \geq 2$, consider the system of $N$ competing species which are ecologically identical and having distinct diffusion rates $\{D_i\}_{i=1}^N$, in an environment with the carrying capacity $m(x,t)$. For a generic class of $m(x,t)$ that varies with space and time, we show that there is a positive number $D_*$ independent of $N$ so that if $D_i \geq D_*$ for all {$1\le i\le N$}, then the slowest diffusing species is able to competitively exclude the rest of the species. In the case when the environment is temporally constant or temporally periodic, our result provides some further evidence in the affirmative direction regarding the conjecture by Dockery et al. in 1998. The main tool is the theory of the principal Floquet bundle for linear parabolic equations. |
|
| 52 |
K.-Y. Lam, Y. Lou and S. Ma, Exploring the evolutionary dynamics of infectious diseases through SIS
epidemic models,
Communications in Information and Systems (CIS) special issue dedicated to Prof. Avner Friedman’s 90th birthday,
23(3) (2023), 289-324.
(DOI 10.4310/CIS.2023.v23.n3.a4).
|
|
| 51 |
D. Gomez, K.-Y. Lam and Y. Mori,
Front Propagation in the Shadow Wave-Pinning Model, J. Math. Biol.,
86, 72 (2023).
(DOI: 10.1007/s00285-023-01908-6).
Highlight: We analyze a simplified version of the wave-pinning model of cell polarization. Daniel was a postdoc with Prof. Yoichiro Mori at U Penn, and since 2024 he is tenure-track assistant professor at U. New Mexico (at Albuquerque, the place of Breaking Bad). 
Read abstractIn this paper we consider a non-local bistable reaction-diffusion equation which is a simplified version of the wave-pinning model of cell polarization. In the small diffusion limit, a typical solution $u(x,t)$ of this model approaches one of the stable states of the bistable nonlinearity in different parts of the spatial domain $\Omega$, separated by an interface moving at a normal velocity regulated by the integral $\int_\Omega u(x,t)\,dx$. In what is often referred to as wave-pinning, feedback between mass-conservation and bistablity causes the interface to slow and approach a fixed limit. In the limit of a small diffusivity $\ep^2\ll 1$, we prove that for any $0<\gamma<1/2$ the interface can be estimated within $O(\ep^\gamma)$ of the location as predicted using formal asymptotics. We also discuss the sharpness of our result by comparing the formal asymptotic results with numerical simulations. |
|
| 50 |
C. Heggerud, K.-Y. Lam and H. Wang,
Niche differentiation in the light spectrum promotes coexistence of phytoplankton species: a spatial modelling approach, J. Math. Biol. 86 (2023), 54.
(With open access)
(DOI 10.1007/s00285-023-01890-z).
Highlights: This collaboration started with a short visit to U. Alberta in Feb 2020, right before the COVID outbreak in North America. Chris was still a grad students then and we study a population structured by space and its preference of light in the entire visible spectrum, and study the competition of different species of phytoplanktons. Chris then did a postdoctoral work with Alan Hastings, and he is a tenure-track faculty at U. Manitoba since 2025. 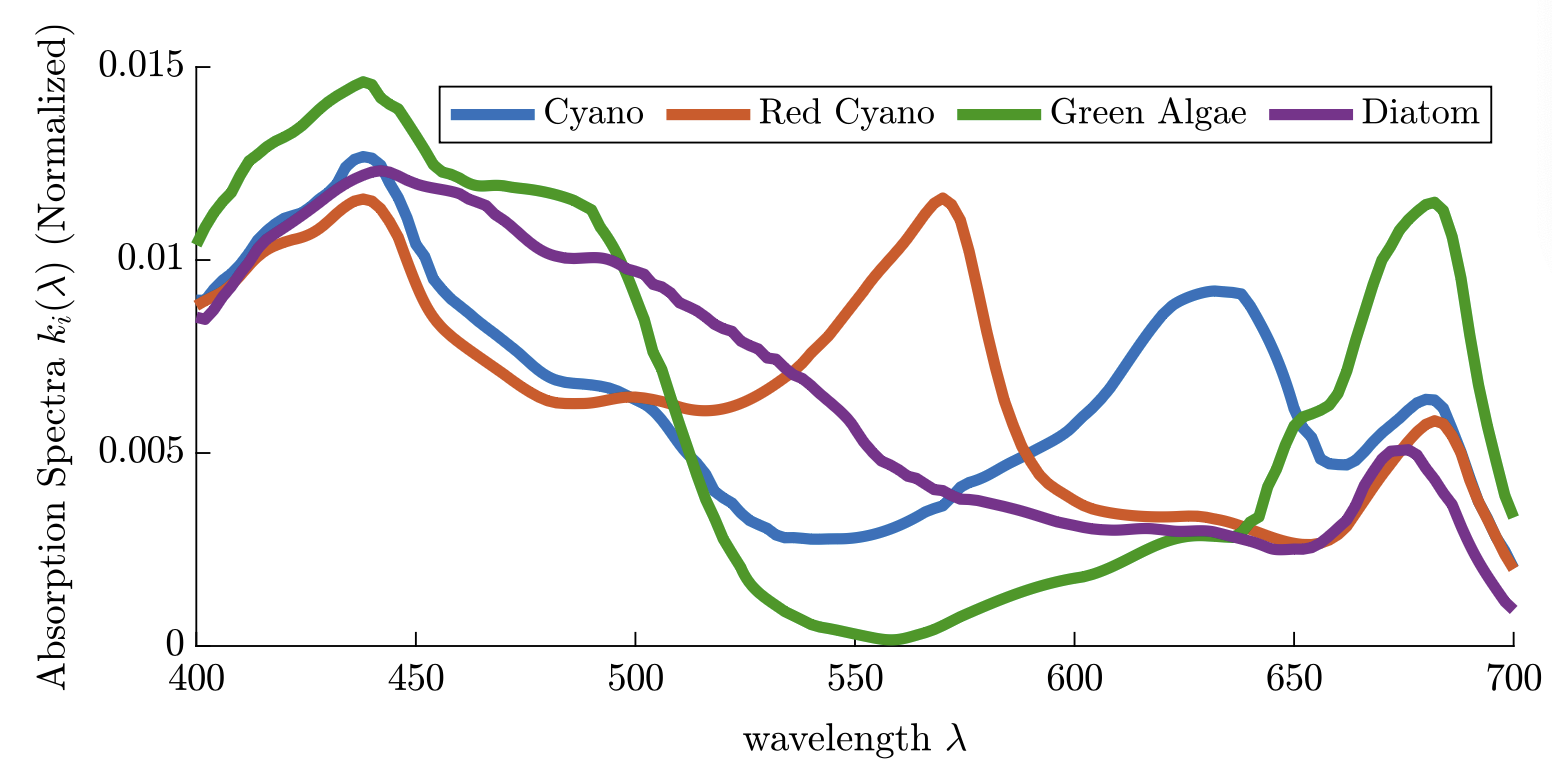
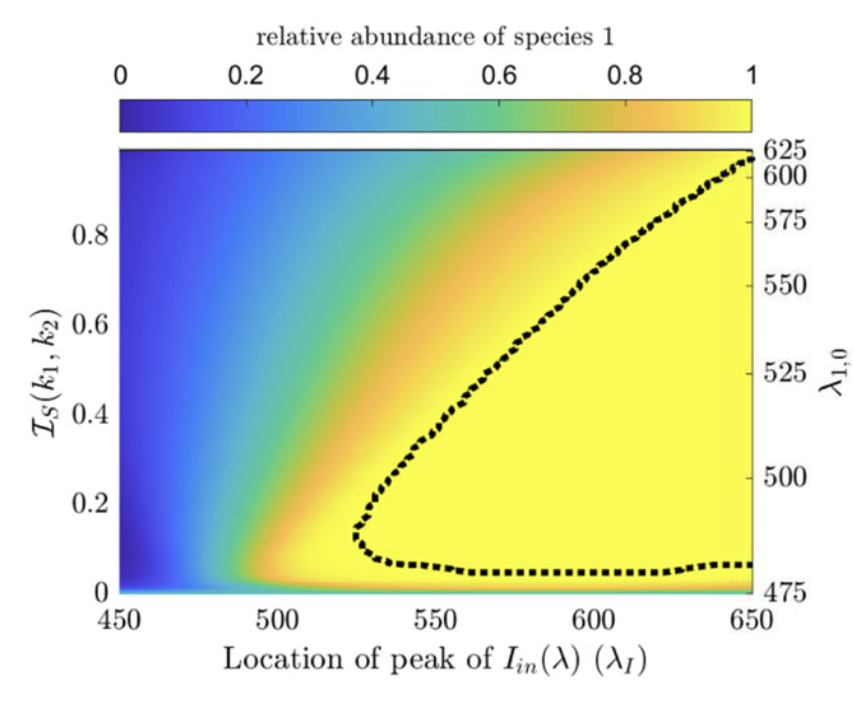
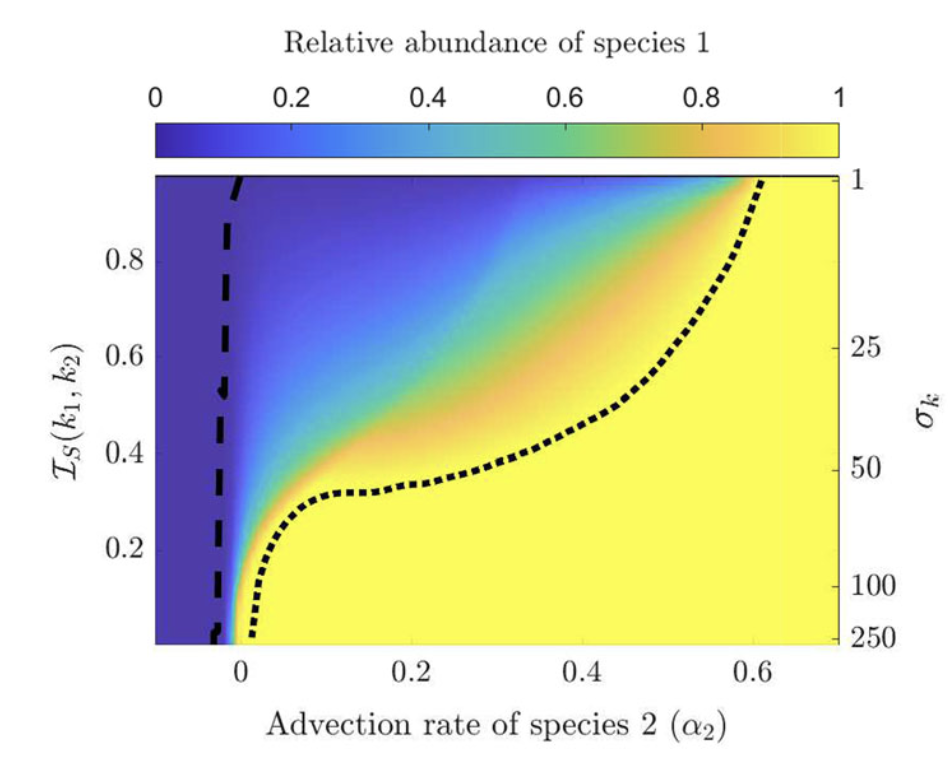
Read abstractThe paradox of the plankton highlights the apparent contradiction between Gause’s law of competitive exclusion and the observed diversity of phytoplankton. It is well known that phytoplankton dynamics depend heavily on light availability. Here we treat light as a continuum of resources rather than a single resource by considering the visible light spectrum. We propose a spatially explicit reaction–diffusion–advection model to explore under what circumstance coexistence is possible from mathematical and biological perspectives. Furthermore, we provide biological context as to when coexistence is expected based on the degree of niche differentiation within the light spectrum and overall turbidity of the water. |
|
| 49 |
K.-Y. Lam, R. Lee and Y. Lou,
Population Dynamics in an Advective Environment, Comm. Appl. Math. Comp., in press.
(DOI 10.1007/s42967-023-00259-9).
Read abstractWe consider a one-dimensional reaction–diffusion equation describing single- and two-species population dynamics in an advective environment, based on the modeling frameworks proposed by Lutscher, Lewis, and McCauley in 2006. We analyze the effect of rate of loss of individuals at both the upstream and downstream boundaries. In the single-species case, we prove the existence of the critical domain size and provide explicit formulas in terms of model parameters. We further derive qualitative properties of the critical domain size and show that, in some cases, the critical domain size is either strictly decreasing over all diffusion rates, or monotonically increasing after first decreasing to a minimum. We also consider competition between species differing only in their diffusion rates. For two species having large diffusion rates, we give a sufficient condition to determine whether the faster or slower diffuser wins the competition. We also briefly discuss applications of these results to competition in species whose spatial niche is affected by shifting isotherms caused by climate change. |
|
48 |
K.-Y. Lam, Y. Lou and B. Perthame,
A Hamilton-Jacobi Approach to Evolution of Dispersal, Comm. Partial Differential Equations, 48(1) (2022) 86-118. (With open access)
(DOI 10.1080/03605302.2022.2139723).
Highlights: In 2022, I was visiting Prof. B. Perthame during my sabbatical and we co-authored a paper on the time-dependent problem featuring moving Dirac solutions. This project started with a question, suggested to us by Prof. Benoit Perthame, of determining the vanishing viscosity limit of structured population models (where the viscosity models mutation rate) way back in 2013. Interestingly, in 2015 two groups (Yuan Lou and myself (see #17) / B. Perthame and P. Souganidis) independently found different solutions to the problem. The paper of Perthame and Souganidis, which uses the Hamilton-Jacobi approach, appeared in Math. Model. Nat. Phenom. in 2016. This is the starting point where I started to become interested in the Hamilton-Jacobi technique, in connection with the principle of selection in biology. Read abstractThe evolution of dispersal is a classical question in evolutionary biology, and it has been studied in a wide range of mathematical models. A selection-mutation model, in which the population is structured by space and a phenotypic trait, with the trait acting directly on the dispersal (diffusion) rate, was formulated by Perthame and Souganidis [Math. Model. Nat. Phenom. 11:154–166, 2016] to study the evolution of random dispersal toward the evolutionarily stable strategy. For the rare mutation limit, it was shown that the equilibrium population concentrates on a single trait associated to the smallest dispersal rate. In this paper, we consider the corresponding evolution equation and characterize the asymptotic behaviors of the time-dependent solutions in the rare mutation limit, under mild convexity assumptions on the underlying Hamiltonian function. |
|
| 47 |
K.-Y. Lam and X. Yu,
Asymptotic spreading of KPP reactive fronts in heterogeneous shifting environments, J. Math. Pures Appl., 167 (2022) 1-47.
(DOI 10.1016/j.matpur.2022.09.001).
Highlights: We study the heterogeneous Fisher-KPP equation with coefficients of the form g(x-ct), with g satisfies a monotone condition. 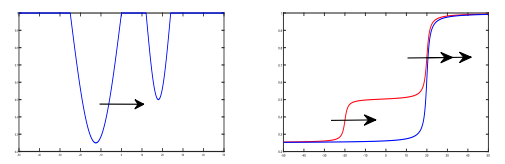
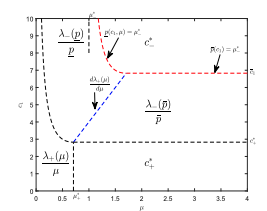
Read abstractWe study the asymptotic spreading of Kolmogorov-Petrovsky-Piskunov (KPP) fronts in heterogeneous shifting habitats, with any number of shifting speeds, by further developing the method based on the theory of viscosity solutions of Hamilton-Jacobi equations. Our framework addresses both reaction-diffusion equation and integro-differential equations with a distributed time-delay. The latter leads to a class of limiting equations of Hamilton-Jacobi-type depending on the variable $x/t$ and in which the time and space derivatives are coupled together. We will first establish uniqueness results for these Hamilton-Jacobi equations using elementary arguments, and then characterize the spreading speed in terms of a reduced equation on a one-dimensional domain in the variable $s=x/t$. In terms of the standard Fisher-KPP equation, our results leads to a new class of ``asymptotically homogeneous" environments which share the same spreading speed with the corresponding homogeneous environments. |
|
| 46 |
A. Friedman, W. Hao and K.-Y. Lam,
A cancer model with nonlocal free boundary dynamics, J. Math. Biol. Vol. 85, Article number: 46 (2022), 28pp.
(DOI 10.1007/s00285-022-01813-4).
Read abstractCancer cells at the tumor boundary move in the direction of \lam{the} oxygen gradient, while cancer cells far within the tumor are in a necrotic state. This paper introduces a simple mathematical model that accounts for these facts. The model consists of cancer cells, cytotoxic T cells, and oxygen satisfying a system of partial differential equations. Some of the model parameters represent the effect of anti-cancer drugs. The tumor boundary is a free boundary whose dynamics is determined by the movement of cancer cells at the boundary. The model is simulated for radially symmetric and axially symmetric tumors, and it is shown that the tumor may increase or decrease \lam{in size,} depending on the ``strength" of the drugs. Existence theorems are proved, global in-time in the radially symmetric case, and local in-time for any shape of tumor. In the radially symmetric case, it is proved, under different conditions, that the tumor may shrink monotonically, or expand monotonically. |
|
| 45 |
B. Zhang, K.-Y. Lam, W.-M. Ni, K. M. Collins, Z. Fu, L. Zhai, Y. Lou, D.L. DeAngelis and A. Hastings, Directed movement changes coexistence outcomes in heterogeneous environments, Ecol. Lett., 25 (2022) 366-377.
(DOI 10.1111/ele.13925).
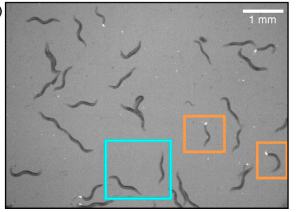
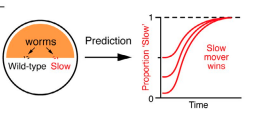
Read abstractUnderstanding the mechanisms that promote coexistence is a central topic in ecology. Among plausible mechanisms of coexistence are different dispersal rates of competing types in heterogeneous environments. A large body of mathematical theory, based on Lotka-Volterra-like equations, proved non-coexistence, with the slower dispersing competitor always excluding the faster disperser. Notably, these results have not been tested empirically and these predictions considered mostly symmetric dispersal. To address these gaps, we not only extended previous theory by including exploitable resources and a component of directed movement, but also tested the new mathematical results experimentally using laboratory populations of the nematode worm, Caenorhaditis elegans. In contrast to previous predictions, our novel results reveal, both theoretically and empirically, that even with different symmetric dispersal, two identical competing species with moderate levels of directed components can coexist. Our results advance coexistence theories and underscore the role of directed dispersal in species coexistence in heterogeneous environments. |
|
| 44 |
S. Liu, Q. Liu and K.-Y. Lam,
Asymptotic spreading of interacting species with multiple fronts II:
Exponentially decaying initial data, J. Differential Equations, 303 (2021) 407-455.
(DOI 10.1016/j.jde.2021.09.023).
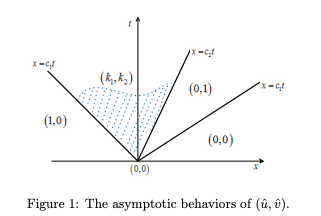
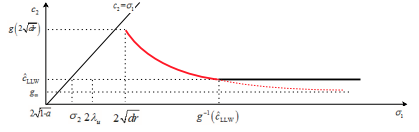
Read abstractThis is part two of our study on the spreading properties of the weak Lotka-Volterra competition-diffusion systems with a stable coexistence state. Here we focus on the case when the initial data are exponential decaying. Here we establish a comparison principle for Hamilton-Jacobi equations, which enable us to adopt the Hamilton-Jacobi approach for Fisher-KPP equation due to Freidlin, Evans and Souganidis. As a result, the exact formulas of spreading speeds and their dependence on initial data are derived. Our results indicate that sometimes the spreading speed of the slower species is nonlocally determined. Connections of our results with the traveling profile due to Tang and Fife, as well as the more recent spreading result of Girardin and Lam, will be discussed. |
|
| 43 |
R.S. Cantrell and K.-Y. Lam,
On the evolution of slow dispersal in multi-species
communities, SIAM Math. Anal., 53(4), 4933–4964. (32 pages)
(DOI 10.1137/20M1361419).
Highlights: We obtain progress on the conjecture of Dockery et al concerning competition of N species which are identical except for their diffusion rate. We show that the set of parameters for which the conjecture holds is open in the Hausdorff sense. To do so, we proved a smooth dependence of Floquet bundle (of linear parabolic equations) on parameters which is of independent interest. Read abstractFor any $N \geq 2$, we show that there are choices of diffusion rates $\{d_i\}_{i=1}^N$ such that for $N$ competing species which are ecologically identical and having distinct diffusion rates, the slowest diffuser is able to competitive exclude the remainder of the species. In fact, the choices of such diffusion rates is open in the Hausdorff topology. Our result provdes some evidence in the affirmative direction regarding the conjecture in [Dockery et al., J. Math. Biol. (1998)]. The main tools include Morse decomposition of the semiflow, as well as the theory of normalized principal bundle for linear parabolic equations. A critical step in the proof is to establish the smooth dependence of the Floquet bundle on diffusion rate and other coefficients, which may be of independent interest. |
|
| 42 |
H. Jiang, K.-Y. Lam and Y. Lou,
Three-patch models for the evolution of dispersal in advective environments: varying drift and network topology, Bull. Math. Biol., 83, 109 (2021).
(DOI 10.1007/s11538-021-00939-8)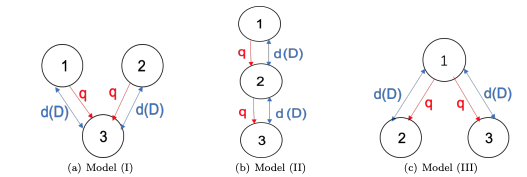
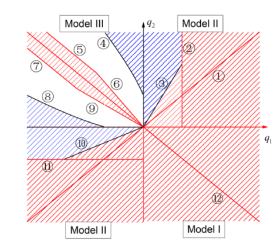
Read abstractWe study the evolution of dispersal in advective three-patch models with distinct network topologies. Organisms can move between connected patches freely and they are also subject to the passive, directed drift. The carrying capacity is assumed to be the same in all patches, while the drift rates could vary. We first show that if all drift rates are the same, the faster dispersal rate is selected for all three models. For general drift rates, we show that the infinite diffusion rate is a local Convergence Stable Strategy (CvSS) for all three models. However, there are notable differences for three models: For Model I, the faster dispersal is always favored, irrespective of the drift rates, and thus the infinity dispersal rate is a global CvSS. In contrast, for Models II and III, a singular strategy will exist for some ranges of drift rates and bi-stability phenomenon happens, i.e. both infinity and zero diffusion rates are local CvSSs. Furthermore, for both Models II and III, it is possible for two competing populations to coexist by varying drift and diffusion rates. Some predictions on the dynamics of $n$-patch models in advective environments are given. |
|
| 41 |
A. Friedman and K.-Y. Lam,
Analysis of a mathematical model of immune response to fungal infection, J. Math. Biol., 83, 8 (2021).
(DOI 10.1007/s00285-021-01633-y).
Read abstractFungi are cells found as commensal residents on the skin and on mucosal surfaces of the human body, including the digestive track and urogenital track, but some species are pathogenic. Fungal infection may spread into deep-seated organs causing life-threatening infection, especially in immune-compromised individuals. Effective defense against fungal infection requires a coordinated response by the innate and adaptive immune systems. In the present paper we introduce a simple model of immune response to fungal infections consisting of three partial differential equations, for the populations of fungi ($F$), neutrophils ($N$) and cytotoxic T cells ($T$), taking $N$ and $T$ to represent, respectively, the innate and adaptive immune cells. We denote by $\lambda_F$ the aggressive proliferation rate of the fungi, by $\eta$ and $\zeta$ the killing rates of fungi by neutrophils and T cells, and by $N_0$ and $T_0$ the immune strengths, respectively, of $N$ and $T$ of an individual. Then take the expression $I=\eta N_0 + \zeta T_0 - \lambda_F$ to represent the coordinated defense of the immune system against fungal infection. We use mathematical analysis to prove the following: If $I>0$, then the infection is eventually stopped and $F \to 0$ as $t \to \infty$; and (ii) if $I<0$ then the infection cannot be stopped and $F$ converges to some positive constant as $t\to\infty$. Treatments of fungal infection include anti-fungal agents and immunotherapy drugs, and both cause the parameter $I$ to increase. This is a post-peer-review, pre-copyedit version of an article published in [insert journal title]. The final authenticated version is available online at: http://dx.doi.org/10.1007/s00285-021-01633-y”. |
|
| 40 |
D. Jiang, Y. Lou and K.-Y. Lam,
Competitive exclusion in a nonlocal reaction-diffusion-advection model of
phytoplankton populations,
Nonlinear Anal. Real World Appl., 61 (2021) 103350, 15pp.
(DOI 10.1016/j.nonrwa.2021.103350).
Read abstractWe continue our study on the global dynamics of a nonlocal reaction-diffusion-advection system modeling the population dynamics of two competing phytoplankton species in an eutrophic environment, where both populations depend solely on light for their metabolism. In our previous work \cite{Jiang2019}, we proved that system \eqref{equ31} is a strongly monotone dynamical system with respect to a non-standard cone related to the cumulative distribution functions, and further determined the global dynamics when the species have either identical diffusion rate or identical advection rate. In this paper, we study the trade-off of diffusion and advection and their joint influence on the outcome of competition. Two critical curves for the local stability of two semi-trivial equilibria are analyzed, and some new competitive exclusion results are obtained. Our main tools, besides the theory of monotone dynamical system, include some new monotonicity results for the principal eigenvalues of elliptic operators in one-dimensional domains. |
|
| 39 |
R.S. Cantrell, C. Cosner and K.-Y. Lam,
Ideal Free Dispersal under General Spatial heterogeneity and Time Periodicity, SIAM J. Appl. Math.,
81 (2021) 789-813.
(DOI 10.1137/20M1332712).
Read abstractA population is said to have an ideal free distribution in a spatially heterogeneous but temporally constant environment if each of its members have chosen a fixed spatial location in a way that optimizes its individual fitness, allowing for the effects of crowding. In this paper, we extend the idea of individual fitness associated with a specific location in space to account for the full path that an individual organism takes in space and time over a periodic cycle, and extend the mathematical formulation of an ideal free distribution to general time periodic environments. We find that, as in many other cases, populations using dispersal strategies that can produce a generalized ideal free distribution have a competitive advantage relative to populations using strategies that do not produce an ideal free distribution. A sharp criterion on the environmental functions is found to be necessary and sufficient for such ideal free distribution to be feasible. In the case the criterion is met, we showed that there exist dispersal strategies that can be identified as producing a time-periodic version of an ideal free distribution, and such strategies are evolutionarily steady and are neighborhood invaders from the viewpoint of adaptive dynamics. Our results extend previous works in which the environments are either temporally constant, or temporally periodic but the total carrying capacity is temporally constant |
|
| 38 |
Q. Liu, S. Liu and K.-Y. Lam Stacked invasion waves in a competition-diffusion model with three species, J. Differential Equations, 271 (2021) 665-718. (DOI 10.1016/j.jde.2020.09.008).
(The slightly longer version, containing the explicit formulas for the nonlocally pulled speed, can be found on arXiv:1910.04217)
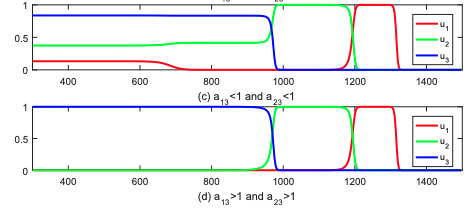
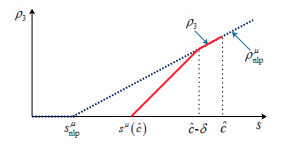
Read abstractWe investigate the spreading properties of a three-species competition-diffusion system, which is non-cooperative. We apply the Hamilton-Jacobi approach, due to Freidlin, Evans and Souganidis, to establish upper and lower estimates of spreading speed of the slowest species, in terms of the spreading speed of two faster species, and show that the estimates are sharp in some situations. The spreading speed will first be characterized as the free boundary point of the viscosity solution for certain variational inequality cast in the space of speeds. Its exact formulas will then be derived by solving the variational inequality explicitly. To the best of our knowledge, this is the first theoretical result on three-species competition system in unbounded domains. |
|
| 37 |
R.S. Cantrell and K.-Y. Lam,
Competitive exclusion in phytoplankton communities in a eutrophic water column, Discrete Contin.Dyn. Syst. Ser. B, 26 (2021), 1783-1795.
(DOI 10.3934/dcdsb.2020361).
Read abstractWe analyze a reaction-diffusion system modeling the competition of multiple phytoplankton species which are limited only by light. While the dynamics of a single species has been well studied, the dynamics of the two-species model has only begun to be understood with the recent establishment of a comparison principle. In this paper, we show that the competition of $N$ similar phytoplankton species, for any number $N$, generically leads to competition exclusion. The main tool is the theory of normalized principal bundle for linear parabolic equations. |
|
| 36 |
W. Hao, K.-Y. Lam and Y. Lou, Ecological and Evolutionary Dynamics in Advective Environments: Critical Domain Size and Boundary Conditions, Discrete Contin. Dyn. Syst. Ser. B, 26 (2021), 367-400 (DOI 10.3934/dcdsb.2020283).
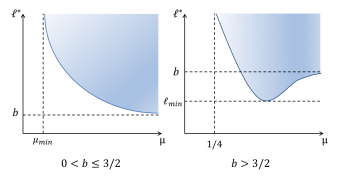
Read abstractWe consider the ecological and evolutionary dynamics of a reaction-diffusion-advection model for populations residing in a one-dimensional advective homogeneous environment, with emphasis on the effects of boundary conditions and domain size. We assume that there is a net loss of populations at the downstream end with rate $b \geq 0$, while the no-flux condition is imposed on the upstream end. For the single species model, it is shown that the critical patch size is a decreasing function of the dispersal rate when $b \leq 3/2$; whereas it first decreases and then increases when $b >3/2$. For the two-species competition model, we show that the infinite dispersal rate is evolutionarily stable for $b < 3/2$ and, when dispersal rates of both species are large, the population with larger dispersal rate always displace the population with smaller rate. For certain specific population loss rate $b<3/2$, it is also shown that there can be up to three evolutionarily stable strategies. For $b>3/2$, it is proved that the infinite random dispersal rate is not evolutionarily stable, and that, for some specific $b>3/2$, a finite dispersal rate is evolutionarily stable. Furthermore, for the intermediate domain size, this dispersal rate is optimal in the sense that the species adopting this rate is able to displace its competitor with a similar but different rate. Finally, nine qualitatively different pairwise invasibility plots are obtained by varying the parameter $b$ and the domain size. |
|
| 35 |
H. Jiang, K.-Y. Lam and Y. Lou, Are two-patch models sufficient? The evolution of dispersal and topology of river network modules, Bull. Math. Biol., 82, Article number: 131 (2020) 34pp. (DOI 10.1007/s11538-020-00803-1)

Read abstractWe study the dynamics of two competing species in three-patch models and illustrate how the topology of directed river network modules may affect the evolution of dispersal. Each model assumes that patch 1 is at the upstream end, patch 3 is at the downstream end, but patch 2 could be upstream, or middle stream, or downstream, depending on the specific topology of the modules. We posit that individuals are subject to both unbiased dispersal between patches and passive drift from one patch to another, depending upon the connectivity of patches. When the drift rate is small, we show that for all models, the mutant species can invade when rare if and only if it is the slower disperser. However, when the drift rate is large, most models predict that the faster disperser wins, while some predict that there exists one evolutionarily singular strategy. The intermediate range of drift is much more complex: most models predict the existence of one singular strategy, but it may or may not be evolutionarily stable, again depending upon the topology of modules, while one model even predicts that for some intermediate drift rate, singular strategy does not exist and the faster disperser wins the competition. This is a post-peer-review, pre-copyedit version of an article published in [insert journal title]. The final authenticated version is available online at: http://dx.doi.org/10.1007/s11538-020-00803-1”. |
|
| 34 |
V. Calvez and K.-Y. Lam,
Uniqueness of the viscosity solution of a constrained Hamilton-Jacobi equation, Calc. Var. Partial Differ. Equ., 59, Article number: 163 (2020) 22pp. (arXiv:1809.05317). (DOI 10.1007/s00526-020-01819-0).
Highlights: This was done while Vincent was visiting Ohio State, when we had the idea to attack the uniqueness of viscosity solution using the Lagrangian view point. This answered a question raised by B. Perthame. 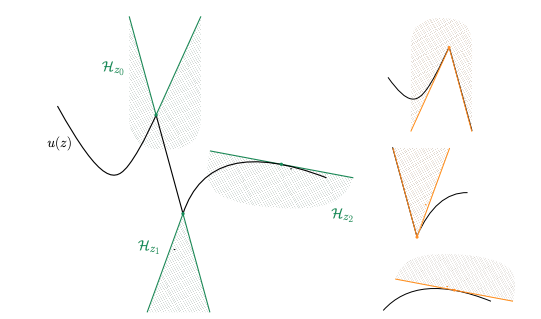
Read abstractIn quantitative genetics, viscosity solutions of Hamilton-Jacobi equations appear naturally in the asymptotic limit of selection-mutation models when the population variance vanishes. They have to be solved together with an unknown function I(t) that arises as the counterpart of a non-negativity constraint on the solution at each time. Although the uniqueness of viscosity solutions is known for many variants of Hamilton-Jacobi equations, the uniqueness for this particular type of constrained problem was not resolved, except in a few particular cases. Here, we provide a general answer to the uniqueness problem, based on three main assumptions: convexity of the Hamiltonian function H(I, x, p) with respect to p, monotonicity of H with respect to I, and BV regularity of I(t). |
|
| 33 48 |
K.-Y. Lam R. Salako, and Q. Wu,
Entire Solutions of Diffusive Lotka-Volterra System,
J. Differential Equations, 269 (2020) 10758-10791.
(10.1016/j.jde.2020.07.006).
Highlights: This was done while Rachidi was Ross Assistant Professor at Ohio State. Since 2020, Rachidi is a faculty at University of Nevada, Las Vegas. 
Read abstractThis work is concerned with the existence of entire solutions of the diffusive Lotka-Volterra competition system. We prove the existence of several new classes of entire solutions. Moreover, we also describe the large-time asymptotic behavior of these entire solutions. In the weak competition case, we prove the existence of a class of entire solutions that forms a 4-dimensional manifold. |
|
| 32 |
A. Friedman and K.-Y. Lam,
Analysis of a mathematical model of rheumatoid arthritis,
J. Math. Biol., 80 (2020) 1857-1883.
(DOI 10.1007/s00285-020-01482-1).
Rheumatoid arthritis is an autoimmune disease characterized by inflammation in the synovial fluid within the synovial joint connecting two contiguous bony surfaces. The inflammation diffuses into the cartilage adjacent to each of the bony surfaces, resulting in their gradual destruction. The interface between the cartilage and the synovial fluid is an evolving free boundary. In this paper we consider a two-phase free boundary problem based on a simplified model of rheumatoid arthritis. We prove global existence and uniqueness of a solution, and derive properties of the free boundary. In particular it is proved that the free boundary increases in time, and the cartilage shrinks to zero as t → ∞, even under treatment by a drug. It is also shown in the reduced one-phased problem, with cartilage alone, that a larger prescribed inflammation function leads to a faster destruction of the cartilage. |
|
31 |
Q. Liu, S. Liu and K.-Y. Lam,
Asymptotic spreading of interacting species with multiple fronts I: A geometric optics approach, Discrete Cont. Dyn. Syst. Ser. A 40 (2020) 3683-3714.
(DOI 10.3934/dcds.2020050).
Read abstractWe establish spreading properties of the Lotka-Volterra competition-diffusion system. When the initial data vanish on a right half-line, we derive the exact spreading speeds and prove the convergence to homogeneous equilibrium states in between the interfaces. Our method is inspired by the geometric optics approach for Fisher-KPP equation due to Freidlin, Evans and Souganidis. Our main result settles an open question raised in a paper of Lin and Li (2012), and show that one of the species spreads to the right with a non-locally determined speed. |
|
| 30 |
L. Girardin and K.-Y. Lam (2019),
Invasion of open space by two competitors: spreading properties of monostable two-species competition-diffusion systems,
Proc. Lond. Math. Soc., 119 (2019), 1279-1335.
(DOI 10.1112/plms.12270).
PLMS Top Downloaded Paper 2018-2019
Highlights: In fall of 2017, Leo visited me in his last year of PhD program as an international experience. He is a highly original mathematician and he essentially introduced me to the field of propagation phenomena. I was very surprised when he told me that the long-time behavior of Lotka-Volterra model, when the initial data of both components are compactly supported, was completely open. We would have lunch and discuss every Monday, Wednesday, Friday. At that time we had little intuition, and our strategy was to "gain intuition" by constructing super/subsolutions. As it turned out, the key to the problem was to capture the interaction between two interfaces that are O(t) apart in the solution. Such interaction is only possible in monotable problems. This paper led to many follow-up works, where we used the Hamilton-Jacobi approach to greatly simplify the proofs. The intuition gained here also led to the construction of different classes of entire solutions for Lotka-Volterra model with diverging fronts (see #33). 
Read abstractThis paper is concerned with some spreading properties of monostable Lotka-Volterra two-species competition-diffusion systems when the initial values are null or exponentially decaying in a right half-line. Thanks to a careful construction of super-solutions and sub-solutions, we improve previously known results and settle open questions. In particular, we show that if the weaker competitor is also the faster one, then it is able to evade the stronger and slower competitor by invading first into unoccupied territories. The pair of speeds depends on the initial values. If these are null in a right half-line, then the first speed is the KPP speed of the fastest competitor and the second speed is given by an exact formula describing the possibility of non- local pulling. Furthermore, the unbounded set of pairs of speeds achievable with exponentially decaying initial values is characterized, up to a negligible set. |
|
| 29 |
D. Jiang, Y. Lou K.-Y. Lam and Z. Wang,
Monotonicity and global dynamics of a nonlocal two-species phytoplankton model,
SIAM J. Appl. Math., 79 (2019), 716-742.
(DOI 10.1137/18M1221588).
Read abstractWe investigate a nonlocal reaction-diffusion-advection system modeling the population dynamics of two competing phytoplankton species in a eutrophic environment, where nutrients are in abundance and the species are limited by light only for their metabolism. We first demonstrate that the system does not preserve the competitive order in the pointwise sense. Then we introduce a special cone K involving the cumulative distributions of the population densities, and a generalized notion of super- and subsolutions of the nonlocal competition system where the differential inequalities hold in the sense of the cone K. A comparison principle is then established for such super- and subsolutions, which implies the monotonicity of the underlying semiflow with respect to the cone K As application, we study the global dynamics of the single species system and the competition system. The latter has implications for the evolution of movement for phytoplankton species. |
|
| 28 |
W. Hao, K.-Y. Lam and Y. Lou,
Concentration phenomena in an integro-PDE model for evolution of conditional dispersal,
Indiana Univ. Math. J., 68 (2019), 881-923.
(DOI 10.1512/iumj.2019.68.7625).
Highlights: We consider an extension of a mutation-selection model first considered by Perthame and Souganidis where the population is structured by space and a continuous trait. We connect mutation-selection models with concepts in adaptive dynamics such as ESS, CSS and evolutionary branching, and quantify the Dirac mass formation as mutation rate goes to zero in the mutation-selection models. Results of possible independent interest can be found in the appendices: (i) a Liouville result for linear elliptic equations in cylinders, and (ii) an extension operator from Neumann boundary data. 
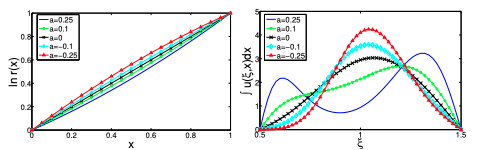
Read abstractTo study the evolution of conditional dispersal we extend the Perthame-Souganidis mutation-selection model and consider an integro-PDE model for a population structured by the spatial variables and one trait vari- able. We assume that both the diffusion rate and advection rate are functions of the trait variable, which lies within a short interval I. Competition for resource is local in spatial variables, but nonlocal in the trait variable. Under proper conditions on the invasion fitness gradient, we show that in the limit of small mutation rate, the positive steady state solution will concentrate in the trait variable and forms (i) a Dirac mass supported at one end of I; or (ii) a Dirac mass supported at the interior of I; or (iii) two Dirac masses supported at both ends of I, respectively. While Cases (i) and (ii) imply the evolutionary stability of a single strategy, Case (iii) suggests that when no single strategy can be evolutionarily stable, it is possible that two peculiar strategies as a pair can be evolutionarily stable and resist the invasion of any other strategy in our context. |
|
| 27 |
L. Su, K.-Y. Lam and R. Bürger,
Two-locus clines maintained by diffusion and recombination in a heterogeneous environment,
J. Differential Equations, 266 (2019), 7909-7947.
(10.1016/j.jde.2018.12.022).
Read abstractWe study existence and stability of stationary solutions of a system of semilinear parabolic partial differential equations that occurs in population genetics. It describes the evolution of gamete frequencies in a geographically structured population of migrating individuals in a bounded habitat. Fitness of individuals is determined additively by two recombining, diallelic genetic loci that are subject to spatially varying selection. Migration is modeled by diffusion. Of most interest are spatially non-constant stationary solutions, so-called clines. In a two-locus cline all four gametes are present in the population, i.e., it is an internal stationary solution. We provide conditions for existence and linear stability of a two-locus cline if recombination is either sufficiently weak or sufficiently strong relative to selection and diffusion. For strong recombination, we also prove uniqueness and global asymptotic stability. For arbitrary recombination, we determine the stability properties of the monomorphic equilibria, which represent fixation of a single gamete. |
|
| 26 |
X. He, K.-Y. Lam, Y. Lou and W.-M. Ni,
Dynamics of a Consumer-Resource Reaction-Diffusion Model,
J. Math. Biol., 78 (2019), 1605-1636.
(DOI 10.1007/s00285-018-1321-z).
Read abstractWe study the dynamics of a consumer-resource reaction-diffusion model, proposed recently by Zhang et al (2017), in both homogeneous and heterogeneous environments. For homogeneous environments we establish the global stability of constant steady states. For heterogeneous environments we study the existence and stability of positive steady states and the persistence of time-dependent solutions. Our results illustrate that for heterogeneous environments there are some parameter regions in which the resources are only partially limited in space, a unique feature which does not occur in homogeneous environments. Such difference between homogeneous and heterogeneous environments seems to be closely connected with a recent finding by Zhang et al (2017), which says that in consumer-resource models, homogeneously distributed resources could support higher population abundance than heterogeneously distributed resources. This is opposite to the prediction by Lou (2006) for logistic-type models. For both small and high yield rates, we also show that when a consumer exists in a region with a heterogeneously distributed input of exploitable renewed limiting resources, the total population abundance at equilibrium can reach a greater abundance when it diffuses than when it does not. In contrast, such phenomenon may fail for intermediate yield rates. This is a post-peer-review, pre-copyedit version of an article published in [insert journal title]. The final authenticated version is available online at: http://dx.doi.org/10.1007/s00285-018-1321-z”. |
|
| 25 |
K.-Y. Lam,
Dirac-concentrations in an Integro-pde Model from Evolutionary Game Theory,
Discrete Cont. Dyn. Syst. Ser. B, 24 (2019), 737-754. (DOI 10.3934/dcdsb.2018205). Highlights: We connect mutation-selection models with concepts in adaptive dynamics such as ESS, CSS and evolutionary branching, and quantify the Dirac mass formation as mutation rate goes to zero in the mutation-selection models. We take the dynamical point of view to construct forward invariant subspaces that contains the stationary Dirac-like solutions. Read abstractNonlocal Lotka-Volterra models have the property that solutions concentrate as Dirac masses in the limit of small diffusion. Motivated by the existence of moving Dirac-concentrations in the time-dependent problem, we study the qualitative properties of steady states in the limit of small diffusion. Under different conditions on the growth rate and interaction kernel as motivated by the framework of adaptive dynamics, we will show that as the diffusion rate tends to zero the steady state concentrates (i) at a single location; (ii) at two locations simultaneously; or (iii) at one of two alternative locations. The third result in particular shows that solutions need not be unique. This marks an important difference of the non-local equation with its local counterpart. |
|
| 24 |
K.-Y. Lam, X. Wang and T. Zhang,
Traveling waves for a class of diffusive disease-transmission models with network structures,
SIAM J. Math. Anal., 50 (2018), 5719-5748.
(DOI 10.1137/17M1144258).Read abstractIn this paper, the necessary and sufficient conditions for the existence of traveling wave solutions are derived for a class of diffusive disease-transmission models with network structures. The existence of traveling semifronts is obtained by Schauder's fixed-point theorem, and these traveling semifronts are shown to be bounded by transforming the boundedness problem into the classification problem of nonnegative solutions to a linear elliptic system on R^1 . To overcome the reducibility problem arising in the proofs, Harnack's inequality for positive supersolutions on R^1 is proved. |
|
| 23 |
R. S. Cantrell, C. Cosner and K.-Y. Lam ,
On resident-invader dynamics in infinite dimensional dynamical systems,
J. Differential Equations, 263 (2017), 4565-4616. (51pp.)
(DOI 10.1016/j.jde.2017.05.029). Highlights: We apply Hadamard's graph transform method to study the competition between two similar species, and extend the Tube Theorem due to Geritz et al. to infinite dimensions. In the appendix, we apply our result to diffusion and nonlocal diffusion model, and a regularity result for nonlocal competition model (showing measurable steady states are in fact continuous) is kind of interesting. 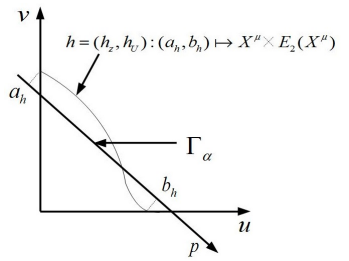
Read abstractMotivated by evolutionary biology, we study general infinite-dimensional dynamical systems involving two species - the resident and the invader. Sufficient conditions for competition exclusion phenomena are given when the two species play similar, but distinct, strategies. Those conditions are based on invasibility criteria, for instance, evolutionarily stable strategies in the framework of adaptive dynamics. These types of questions were first proposed and studied by [S. Geritz et al., J. Math. Biol., 2002] and [S. Geritz, J. Math. Biol., 2005] for a class of ordinary differential equa- tions. We extend and generalize previous work in two directions. Firstly, we consider analytic semiflows in infinite-dimensional spaces. Secondly, we devise an argument based on Hadamard’s graph transform method that does not depend on the monotonicity of the two-species system. Our results are applicable to a wide class of reaction-diffusion models as well as models with nonlocal diffusion operators. |
|
| 22 |
H.-B. Hsu, K.-Y. Lam and F.-B. Wang,
Single species growth consuming inorganic carbon with internal storage in the unstirred chemostat,
J. Math. Biol., 75 (2017), 1775-1825. (51pp.)
(DOI 10.1007/s00285-017-1134-5). Highlights: We introduce the version of Krein-Rutman theorem for (nonlinear) homogeneous operators involving two cones to completely characterize the persistence criterion of a ratio dependent PDE system. For such system, it is impossible to linearize at the trivial solution. Special thanks to Prof. Horst Thieme for suggesting very useful literature of the theory. This work is initiated when I was visiting Prof. Sze-Bi Hsu who was director of NCTS that was at National Tsing-Hua University in Taiwan at the time. Read abstractThis paper presents a PDE system modeling the growth of a single species population consuming inorganic carbon that is stored internally in a poorly mixed habitat. Inorganic carbon takes the forms of “CO2” (dissolved CO2 and carbonic acid) and “CARB” (bicarbonate and carbonate ions), which are substitutable in their effects on algal growth. We first establish a threshold type result on the extinction/persistence of the species in terms of the sign of a principal eigenvalue associated with a nonlinear eigenvalue problem. If the habitat is the unstirred chemostat, we add biologically relevant assumptions on the uptake functions and prove the uniqueness and global attractivity of the positive steady state when the species persists. This is a post-peer-review, pre-copyedit version of an article published in [insert journal title]. The final authenticated version is available online at: http://dx.doi.org/10.1007/s00285-017-1134-5”. |
|
| 21 |
K.-Y. Lam,
Stability of Dirac Concentrations in an Integro-PDE Model for Evolution of Dispersal,
Calc. Var. Partial Differ. Equ., (2017) 56: 79. (DOI 10.1007/s00526-017-1157-1). Highlights: This paper originated from a question of Prof. Michael Winkler concerning the uniqueness of stationary Dirac-like solutions in selection mutation models at an AIMS conference. (The uniqueness follows as a consequence of stability.) Read abstractWe consider an integro-PDE model from evolutionary biology. The solution u(x,a) structured by two variables x and alpha. The diffusion coefficient in the x direction depends on a and the diffusion coefficient in the α direction is a constant epsilon. A special feature of this model is the appearance of the integral of the solution in the alpha variable, which can be viewed as an infinite dimensional parameter of the problem. In a previous work, the existence of a steady state that exhibits Dirac-concentration in one of the variables yet remains regular in the other variables was proved independently by [Lam and Lou, J. Funct. Anal. (2017)] and [Perthame and Souganidies, arXiv:1505.03420 (2015)]. In this paper, we tackle the long-time dynamics of solutions. When the environment function is non-constant, we show that the steady state is linearly stable by considering the corresponding nonlocal eigenvalue problem. Uniqueness of steady state is obtained from the stability result via a degree argument. When the environment function is constant, the global asymptotic stability result is obtained. This problem can be regarded as a competition of infinitely many species parameterized by α. As with the competition model for three or more species, the integro-PDE model does not generate a monotone dynamical system so that it is necessary to consider all (real or complex) eigenvalues in determining its linear stability. |
|
| 20 |
R. Cui, K.-Y. Lam and Y. Lou,
Dynamics and Asymptotic Profiles of Steady States of an Epidemic Model in Advective Environments,
J. Differential Equations, 263 (2017), 2343-2373.
(10.1016/j.jde.2017.03.045) Highlights: Highly cited paper according to the Web of Science. Read abstractWe study the dynamics of a SIS epidemic model of reaction-diffusion-advection type. The persistence of infected and susceptible populations and the global stability of the disease free equilibrium are established when the basic reproduction number is greater than or less than or equal to one, respectively. We further consider the effects of diffusion and advection on asymptotic profiles of endemic equilibrium: When the advection rate is relatively large comparing to the diffusion rates of both populations, then two populations persist and concentrate at the downstream end. As the diffusion rate of the susceptible population tends to zero, the density of the infected population decays exponentially for positive advection rate but linearly when there is no advection. Our results suggest that advection can help speed up the elimination of disease. |
|
| 19 |
M. Golubitsky, W. Hao, K.-Y. Lam and Y. Lou,
Dimorphism by singularity theory in a model for river ecology,
Bull. Math. Biol., 79 (2017), 1051-1069.
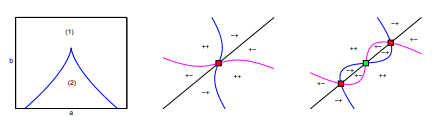
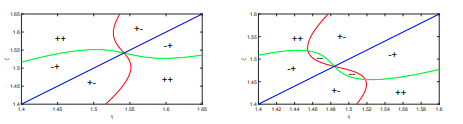
Read abstractGeritz, Gyllenberg, Jacobs, and Parvinen show that two similar species can coexist only if their strategies are in a sector of parameter space near a nondegenerate evolutionarily singular strategy. We show that the dimorphism region can be more general by using the unfolding theory of Wang and Golubitsky near a degenerate evolutionarily singular strategy. Specifically, we use a PDE model of river species as an example of this approach. Our find- ing shows that the dimorphism region can exhibit various different forms that are strikingly different from previously known results in adaptive dynamics. This is a post-peer-review, pre-copyedit version of an article published in [insert journal title]. The final authenticated version is available online at: http://rdcu.be/J6M3”. |
|
| 18 |
R.S. Cantrell, X. Cao, K.-Y. Lam and T. Xiang,
A PDE model of intraguild predation with cross-diffusion,
Discrete Contin. Dyn. Syst. Ser. B, 22 (2017), 3653-3661.
(DOI 10.3934/dcdsb.2017145) Read abstractThis note concerns a quasilinear parabolic system modeling an intraguild predation community in a focal habitat in Rn, n greater than or equal to 2. In this system the intraguild prey employs a fitness-based dispersal strategy whereby the in- traguild prey moves away from a locale when predation risk is high enough to render the locale undesirable for resource acquisition. The system modifies the model considered in Ryan and Cantrell (2015) by adding an element of mutual interference among predators to the functional response terms in the model, thereby switching from Holling II forms to Beddington-DeAngelis forms. We show that the resulting system can be realized as a semi-dynamical system with a global attractor for any n greater than or equal to 2. In contrast, the orginal model was restricted to two dimensional spatial habitats. The permanance of the intraguild prey then follows as in Ryan and Cantrell by means of the Acyclicity Theorem of Persistence Theory. |
|
17 |
K.-Y. Lam and Y. Lou,
An integro-PDE model for evolution of random dispersal,
J. Funct. Anal., 272 (2017), 1755-1790.
(DOI 10.1016/j.jfa.2016.11.017)
Highlights: This is a question, suggested to us by Prof. Benoit Perthame, of determining the vanishing viscosity limit of structured population models (where the viscosity models mutation rate) in 2013. Interestingly, in 2015 two groups (Yuan Lou and myself / B. Perthame and P. Souganidis) independently found different solutions to the problem. The paper, which uses the Hamilton-Jacobi approach, appeared in Math. Model. Nat. Phenom. in 2016. This is the starting point where I started to become interested in the Hamilton-Jacobi technique, in connection with the principle of selection in biology. In 2022, I was visiting Prof. B. Perthame during my sabbatical and we co-authored a paper on the time-dependent problem featuring moving Dirac solutions (see #48) Read abstractWe consider an integro-PDE model for a population structured by the spatial variables and a trait variable which is the diffusion rate. Competition for resource is local in spatial variables, but nonlocal in the trait variable. We focus on the asymptotic profile of positive steady state solutions. Our result shows that in the limit of small mutation rate, the solution remains regular in the spatial variables and yet concentrates in the trait variable and forms a Dirac mass supported at the lowest diffusion rate. Hastings and Dockery et al. showed that for two competing species in spatially heterogeneous but temporally constant environment, the slower diffuser always prevails, if all other things are held equal. Our result suggests that their findings may well hold for arbitrarily many or even a continuum of traits. |
|
| 16 |
I. Averill, K.-Y. Lam and Y. Lou,
The role of advection in a two-species competition model: a bifurcation approach,
Mem. Amer. Math. Soc., Vol. 245 (2017), no. 1161, v+117pp.
(DOI 10.1090/memo/1161) 


Read abstractThe effects of weak and strong advection on the dynamics of reaction- diffusion models have long been studied. In contrast, the role of intermediate advec- tion remains poorly understood. For example, concentration phenomena can occur when advection is strong, providing a mechanism for the coexistence of multiple populations, in contrast with the situation of weak advection where coexistence may not be possible. The transition of the dynamics from weak to strong advection is generally difficult to determine. In this work we consider a mathematical model of two competing populations in a spatially varying but temporally constant environment, where both species have the same population dynamics but different dispersal strategies: one species adopts random dispersal, while the dispersal strategy for the other species is a combination of random dispersal and advection upward along the resource gradient. For any given diffusion rates we consider the bifurcation diagram of positive steady states by using the advection rate as the bifurcation parameter. This approach enables us to capture the change of dynamics from weak advection to strong advection. We will determine three different types of bifurcation diagrams, depending on the difference of diffusion rates. Some exact multiplicity results about bifurcation points will also be presented. Our results can unify some previous work and, as a case study about the role of advection, also contribute to our understanding of intermediate (relative to diffusion) advection in reaction-diffusion models. |
|
| 15 |
K.-Y. Lam, Y. Lou and F. Lutscher,
The emergence of range limits in advective environments,
SIAM J. Appl. Math., 76 (2016), 641-662.
(DOI 10.1137/15M1027887) Read abstractIn this paper, we study the asymptotic profile of the steady state of a reaction- diffusion-advection model in ecology proposed in [E. Pachepsky et al., Theoret. Popul. Biol., 67 (2005), pp. 61–73; D. Speirs and W. Gurney, Ecology, 82 (2001), pp. 1219–1237]. The model de- scribes the population dynamics of a single species experiencing a unidirectional flow. We show the existence of one or more internal transition layers and determine their locations. Such locations can be understood as the upstream invasion limits of the species. It turns out that these invasion limits are connected to the upstream spreading speed of the species and are sometimes subject to the effect of migration from upstream source patches. |
|
| 14 |
K.-Y. Lam and Y. Lou,
Asymptotic behavior of the principal eigenvalue for cooperative elliptic systems and applications,
J. Dynam. Differential Equations, 28 (2016), 29-48.
(DOI 10.1007/s10884-015-9504-4)Read abstractThe asymptotic behavior of the principal eigenvalue for general linear cooperative elliptic systems with small diffusion rates is determined. As an application, we show that if a cooperative system of ordinary differential equations has a unique positive equilibrium which is globally asymptotically stable, then the corresponding reaction-diffusion system with either the Neumann boundary condition or the Robin boundary condition also has a unique positive steady state which is globally asymptotically stable, provided that the diffusion coefficients are sufficiently small. Moreover, as the diffusion coefficients approach zero, the positive steady state of the reaction-diffusion system converges uniformly to the equilibrium of the corresponding kinetic system. |
|
| 13 |
K.-Y. Lam and D. Munther,
A Remark on the Global Dynamics of Competitive Systems on Ordered Banach Spaces,
Proc. Amer. Math. Soc. 144 (2016), 1153-1159.
(DOI 10.1090/proc12768)
Read abstractA well-known result in [Hsu-Smith-Waltman, Trans. AMS (1996)] states that in a competitive semiflow defined on X+ = X1+ ×X2+, the product of two cones in respective Banach spaces, if (u∗,0) and (0,v∗) are the global attractors in X1+ × {0} and {0} × X2+ respectively, then one of the following three outcomes is possible for the two competitors: either there is at least one coexistence steady state, or one of (u∗,0),(0,v∗) attracts all trajectories initiating in the order interval I = [0, u∗] × [0, v∗]. However, it was demon- strated by an example that in some cases neither (u∗,0) nor (0,v∗) is globally asymptotically stable if we broaden our scope to all of X+. In this paper, we give two sufficient conditions that guarantee, in the absence of coexistence steady states, the global asymptotic stability of one of (u∗, 0) or (0, v∗) among all trajectories in X+. Namely, one of (u∗,0) or (0,v∗) is (i) linearly unsta- ble, or (ii) is linearly neutrally stable but zero is a simple eigenvalue. Our results complement the counter example mentioned in the above paper as well as applications that frequently arise in practice. |
|
| 12 |
A. Friedman and K.-Y. Lam,
Analysis of a free-boundary tumor model with angiogenesis,
J. Differential Equations 259 (2015), 7636-7661.
(DOI 10.1016/j.jde.2015.08.032) Read abstractWe consider a free boundary problem for a spherically symmetric tumor with free boundary. In order to receive nutrients u the tumor attracts blood vessel at a rate proportional to a given function alpha(t), so that a robin condition holds on the boundary depending on the nutrient concentration outside the tumor. A parameter in the model is proportional to the ‘aggressiveness’ of the tumor. When alpha is a constant, the existence and uniqueness of stationary solution is proved. For the more general situation when alpha depends on time, we show, under various conditions that (i) R(t) remains bounded if alpha(t) remains bounded; (ii) R(t) --> 0 if alpha(t) -->0; and (iii) liminf R(t) > 0 if liminf alpha(t) > 0. Surprisingly, we exhibit solutions where alpha(t) --> 0 exponentially in t while R(t) --> infinity exponentially in t. Finally, we prove the global asymptotic stability of steady state when μ is sufficiently small. |
|
| 11 |
K.-Y. Lam, Y. Lou and F. Lutscher ,
Evolution of dispersal in closed advective environments,
J. Biol. Dyn. 9 Suppl. 1 (2014), 188-212.
(DOI 10.1080/17513758.2014.969336) Read abstractWe study a two-species competition model in a closed advective environment, where individuals are exposed to unidirectional flow (advection) but no individuals are lost through the boundary. The two species have the same growth and advection rates but different random dispersal rates. The linear stability analysis of the semi-trivial steady state suggests that, in contrast to the case without advection, slow dispersal is generally selected against in closed advective environments. We investigate the invasion exponent for various types of resource functions, and our analysis suggests that there might exist some intermediate dispersal rate that will be selected. When the diffusion and advection rates are small and comparable, we determine criteria for the existence and multiplicity of singular strategies and evolutionarily stable strategies. We further show that every singular strategy is convergent stable. |
|
| 10 |
K.-Y. Lam and W.-M. Ni,
Advection-mediated competition in general environments,
J. Differential Equations, 257 (2014), 3466-3500.
(DOI 10.1016/j.jde.2014.06.019) Read abstractWe consider a reaction-diffusion-advection system of two competing species with one of the species dispersing by random diffusion as well as a biased movement upward along resource gradient, while the other species by random diffusion only. It has been shown that, under some non-degeneracy conditions on the environment function, the two species always coexist when the advection is strong. In this paper, we show that for general smooth environment function, in contrast to what is known, there can be competitive exclusion when the advection is strong, and, we give a sharp criterion for coexistence that includes all previously considered cases. Moreover, when the domain is one-dimensional, we derive in the strong advection limit a system of two equations defined on different domains. Uniqueness of steady states of this non-standard system is obtained when one of the diffusion rates is large. |
|
| 9 |
A. Friedman and K.-Y. Lam,
On the stability of steady states in a granuloma model,
J. Differential Equations, 256 (2014), 3743-3769.
(DOI 10.1016/j.jde.2014.02.019) Read abstractWe consider a free boundary problem for a system of two semilinear parabolic equations. The system represents a simple model of granuloma, a collection of immune cells and bacteria filling a 3- dimensional domain which varies in time. We prove the existence of stationary spherical solutions and study their linear asymptotic stability as time increases to infinity. |
|
| 8 |
K.-Y. Lam and D. Munther,
Invading the ideal free distribution, Special Issue in Honor of Chris Cosner's 60th Birthday ,
Discrete Contin. Dyn. Syst. Ser. B, 19 (2014), 3219-3244.
(DOI 10.3934/dcdsb.2014.19.3219) Read abstractRecently, the ideal free dispersal strategy has been proven to be evolutionarily stable in the spatially discrete as well as continuous setting. That is, at equilibrium a species adopting the strategy is immune against invasion by any species carrying a different dispersal strategy, other conditions being held equal. In this paper, we consider a two-species competition model where one of the species adopts an ideal free dispersal strategy, but is penalized by a weak Allee effect. We will show rigorously in this case that the ideal free disperser is invasible by a range of non-ideal free strategies, illustrating the trade-off between the advantage of being an ideal free disperser and the setback caused by the weak Alee effect. Moreover, a sharp integral criterion is given to determine the stability/instability of one of the semi-trivial steady state, which is always linearly neutrally stable due to the degeneracy caused by the weak Allee effect. |
|
| 7 |
K.-Y. Lam and Y. Lou,
Evolutionarily stable and convergent stable strategies in
reaction-diffusion models for conditional dispersal,
Bull. Math. Biol.,76 (2014), 261-291.
(DOI 10.1007/s11538-013-9901-y)
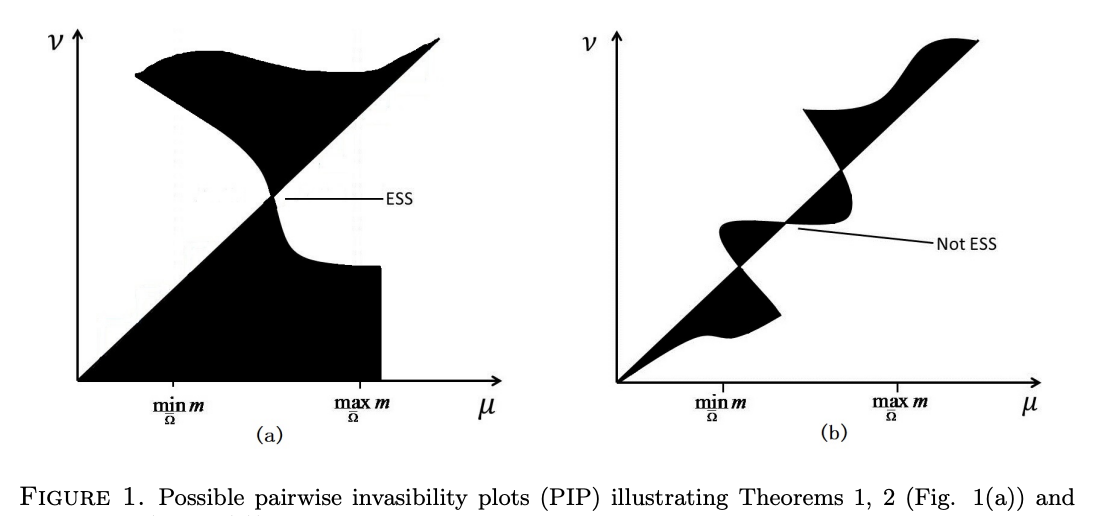
Read abstractWe consider a mathematical model of two competing species for the evolution of conditional dispersal in a spatially varying but temporally constant environment. Two species are different only in their dispersal strategies, which are a combination of random dispersal and biased movement upward along the resource gradient. In the absence of biased movement or advection, Hastings showed that the mutant can invade when rare if and only if it has smaller random dispersal rate than the resident. When there is a small amount of biased movement or advection, we show that there is a positive random dispersal rate that is both locally evolutionarily stable and convergent stable. Our analysis of the model suggests that a balanced combination of random and biased movement might be a better habitat selection strategy for populations. This is a post-peer-review, pre-copyedit version of an article published in [insert journal title]. The final authenticated version is available online at: http://dx.doi.org/10.1007/s11538-013-9901-y”. |
|
| 6 |
K.-Y. Lam and Y. Lou,
Evolution of dispersal: ESS in spatial models,
J. Math. Biol., 68 (2014), 851-877.
(DOI 10.1007/s00285-013-0650-1)
Read abstractWe consider a two-species competition model in which the species have the same population dynamics but different dispersal strategies. Both species disperse by a combination of random diffusion and advection along environmental gradients, with the same random dispersal rates but different advection coefficients. Regarding these advection coefficients as movement strategies of the species, we investigate their course of evolution. By applying invasion analysis we find that if the spatial environmental variation is less than a critical value, there is a unique evolutionarily singular strategy, which is also evolutionarily stable. If the spatial environmental variation exceeds the critical value, there can be at least three evolutionarily singular strategies, one of which is not evolutionarily stable. Our results suggest that the evolution of conditional dispersal of organisms depends upon the spatial heterogeneity of the environment in a subtle way This is a post-peer-review, pre-copyedit version of an article published in [insert journal title]. The final authenticated version is available online at: http://dx.doi.org/10.1007/s00285-013-0650-1”. |
|
| 5 |
K.-Y. Lam,
Limiting Profiles of semilinear elliptic equations with large advection in population dynamics II,
SIAM J. Math. Anal., 44 (2012), 1808-1830.
(DOI 10.1137/100819758)
Read abstractLimiting profiles of solutions to a 2x2 Lotka–Volterra competition-diffusion-advection system, when the strength of the advection tends to infinity, are determined. The two species, competing in a heterogeneous environment, are identical except for their dispersal strategies: one is just a random diffusion, while the other is “smarter”—a combination of random diffusion and a directed movement up the environmental gradient. In the previous paper of Lam and Ni [Discrete Contin. Dyn. Syst. 28 (2010), pp. 1051–1067], it is proved that in one space dimension, for large advection the “smarter” species concentrates near a selected subset of positive local maximum points of the environment function, establishing a conjecture proposed by Cantrell, Cosner, and Lou. With a different method, we generalize this result to any dimensions with the peaks located under mild hypotheses on the environment function. Moreover, a Liouville-type result which gives the asymptotic profile is proved. |
|
| 4 |
K.-Y. Lam and W.-M. Ni,
Uniqueness and complete dynamics of the Lotka-Volterra competition diffusion system,
SIAM J. Appl. Math., 72 (2012), no.6, 1695-1712.
(DOI 10.1137/120869481)Read abstractIn this paper we study the interactions between diffusion and heterogeneity of the environment in the classical diffusive Lotka-Volterra competition systems. In the weak competition case, we establish the uniqueness, hence the global asymptotic stability, of coexistence steady states under various circumstances, and thereby we obtain a complete understanding of the change in dynamics when one of the interspecific competition coefficients is smal |
|
| 3 |
X. Chen, K.-Y. Lam and Y. Lou,
Dynamics of a reaction-diffusion-advection model for two competing species,
Discrete Contin. Dyn. Syst. A, 32 (2012), 3841-3859.
(DOI 10.3934/dcds.2012.32.3841) Highlights: This paper was initiated in a conference organized by Yuan Lou and Avner Friedman at the NCTS in Taiwan in December 2010. There, Xinfu Chen, Yuan Lou and I discussed the ideas of my thesis concerning the construction of a supersolution for an equation with large advection using gluing. Three days later, Xinfu hand me a few pages of yellow legal pad paper with a much nicer concise construction and the three of us write it up later. Part of this work is also done while Prof. Wei-Ming Ni and I drove from Minnesota together to visit Yuan Lou for 4 weeks in May 2011. About the corrigendum: Our construction was fine, we were just wrong about citing a few theorems from Lopez-Gomez as those theorem requires smooth boundary. In the corrigendum, we explain why we can do with less smoothness of the boundary and our result stands with those references being removed. Read abstractWe study the dynamics of a reaction-diffusion-advection model for two competing species in a spatially heterogeneous environment. The two species are assumed to have the same population dynamics but different dispersal strategies: both species disperse by random diffusion and advection along the environmental gradient, but with different random dispersal and/or advection rates. Given any advection rates, we show that three scenarios can occur: (i) If one random dispersal rate is small and the other is large, two competing species coexist; (ii) If both random dispersal rates are large, the species with much larger random dispersal rate is driven to extinction; (iii) If both random dispersal rates are small, the species with much smaller random dispersal rate goes to extinction. Our results suggest that if both advection rates are positive and equal, an intermediate random dispersal rate may evolve. This is in contrast to the case when both advection rates are zero, where the species with larger random dispersal rate is always driven to extinction. |
Corrig. |
| 2 |
K.-Y. Lam and W.-M. Ni,
Limiting profiles of semilinear elliptic equations with large advection in population dynamics, Special Volume in Honor of Louis Nirenberg's 85th Birthday,
Discrete Contin. Dyn. Syst. A 28 (2010), no. 3, 1051-1067.
(DOI 10.3934/dcds.2010.28.1051) Read abstractLimiting profiles of solutions to a 2X2 Lotka-Volterra competition-diffusion-advection system, when the strength of the advection tends to infinity, are determined. The two species, competing in a heterogeneous environment, are identical except for their dispersal strategies: One is just random diffusion while the other is smarter - a combination of random diffusion and a directed movement up the environmental gradient. With important progress made, it has been conjectured in [2] and [3] that for large advection the smarter species will concentrate near a selected subset of positive local maximum points of the environment function. In this paper, we establish this conjecture in one space dimension, with the peaks located and the limiting profiles determined, under mild hypotheses on the environment function. |
|
| 1 |
K.-Y. Lam,
Concentration phenomena of a semilinear elliptic equation with large advection in an ecological model,
J. Differential Equations, 250 (2011), no. 1, 161-181.
(DOI 10.1016/j.jde.2010.08.028) Read abstractWe consider a reaction-diffusion-advection equation arising from a biological model of migrating species. The qualitative properties of the globally attracting solution are studied and in some cases the limiting profile is determined. In particular, a conjecture of Cantrell, Cosner and Lou on concentration phenomena is resolved under mild conditions. Applications to a related parabolic competition system are also discussed. |
Doctoral Thesis:
Collaborators:
|
Wei-Ming Ni 倪维明 Yuan Lou 楼元 Dan Munther Isabel Averill Shuang Liu 刘爽
Qian Liu 刘钱
thesis
Hongyan JiangShizhao Ma 马士召 Xiaoqing He 何小清 Linlin Su 苏琳琳
Ray Lee
thesis
Lin Wang 汪林De Tang 唐徳 Hua Zhang 张华 Rashidi Salako |
Avner Friedman Xinfu Chen 陈新富 Wenrui Hao 郝文瑞 Zhi-Cheng Wang 王智诚 Renhao Cui 崔仁浩 Qiliang Wu 吴启亮 Hao Wang Chris Heggerud Yurij Salmaniw Xiao-Qiang Zhao 赵晓强 Yu Xiao 余虓 Min Zhu 朱敏 Zhi-An Wang 王治安 Hai-Yang Jin 金海洋
Jia-Wei Chu 储佳玮
thesis |
Steve Cantrell Chris Cosner Sze-Bi Hsu 许世璧 Feng-Bin Wang 王埄彬 Chang-Hong Wu 吳昌鴻 Xinru Cao 曹欣茹 Tian Xiang 向田 Don DeAngelis Bo Zhang 张波 Jamaal Jacobs Ashley Baragary Kevin Collins Alan Hastings Lu Zhai 翟路 Danhua Jiang 蒋丹华 |
Reinhard Bürger Benoît Perthame Vincent Calvez Chris Henderson Idriss Mazari Frithjof Lutscher Marty Golubitsky Daniel Gomez Yoichiro Mori 森 洋一朗 Xueying Wang 王雪莹 Tianran Zhang 张天然 Yaping Wu 吴雅萍 Qing Li 李青 Grégoire Nadin |
Notes:
1. On Cooperative elliptic systems: Principal eigenvalue and characterization of the maximum principle. (PDF) This is a note based on my lecture at Center for PDE in East China Normal Unviersity. In this note, the theory of principal eigenvalue of cooperative systems via the Krein-Rutman Theorem, as well as the characterization of maximum principle for such systems are developed.
Read abstract
2. A note on existence of complete Lyapunov function. (PDF) In this note we presents a self-contained proof for the existence of complete Lyapunov function for semiflow admitting a Morse decomposition. The main references are C. Conley's CBMS lecture notes and the monograph by K.P. Rybakowski.
Read abstract
3. A note on critical slope lemmas due to Imbert & Monneau. (PDF) In this note we presents a proof for the critical slope lemmas which is highly useful in the theory of flux-limited solution for Hamilton-Jacobi equations. The proof is taken directly from [Imbert-Monneau, 2017].
Read abstract
3. A note on the comparison principle we used in [Henderson-Lam, JMPA, 2025]. (PDF) In this note we presents a proof for the comparison principle for Flux-Limited solutions of Hamitlon-Jaocbo equations on domains with junction conditions. We follow the ideas of Lions and Sougandis to convert the junction conditions to Kirchhoff (Neumann) conditions.
Read abstract
4. A note on properties of limit set I wrote for my graduate ODE class. (PDF) In this note we presents a proof for some common properties (compact, connected, invariant, etc.) and point out a gap in Schaeffer and Cain with a counter example that those properties may not hold when trajectories are not compact.
Read abstract
Publications under NSF Grant DMS-1411476 (2014-2018)
 88th Midwest PDE Seminar
88th Midwest PDE Seminar Location: Ohio State University,
Columbus, OH
Date: April 26-28, 2024
Co-organize with Bo Guan, John Holmes, Yulong Xing
Registration/Workshop URL
 BIRS Workshop: Dynamical Models Inspired by Biology (24w5209)
BIRS Workshop: Dynamical Models Inspired by Biology (24w5209) Location: Banff International Research Station
Banff National Park, Canada
Date: October 6-11, 2024
Co-organize with Avner Friedman, Yuan Lou, Bo Zhang, Bei Hu and Vincent Calvez
 IMSI Workshop: Mathematical Modeling of Biological Interfacial Phenomena
IMSI Workshop: Mathematical Modeling of Biological Interfacial Phenomena Location: IMSI, University of Chicago
Chicago, IL
Date: Dec 9-13, 2024
Co-organize with Bei Hu and Benoit Perthame
 Short course at the 2022 Spring Trimester Program at
Short course at the 2022 Spring Trimester Program at Institut Henri Poinaré: Mathematical modeling of organization in living matter
Link to the program
Link to the course materials